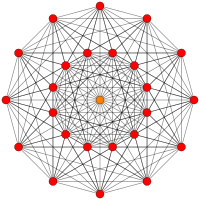
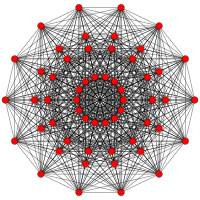
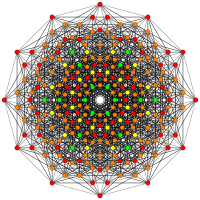
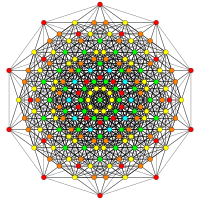
3 21 polytope
| ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Read other articles:

AheGambar atol Ahe yang diambil NASAAheGeografiLokasiSamudra PasifikKoordinat14°29′S 146°19′W / 14.483°S 146.317°W / -14.483; -146.317Koordinat: 14°29′S 146°19′W / 14.483°S 146.317°W / -14.483; -146.317KepulauanTuamotuLuas138 km2 (lagoon)12 km2 (5 sq mi)Panjang23.5 kmLebar12.2 kmTitik tertinggi(tak bernama) (10 m)PemerintahanNegara PrancisWilayah seberang laut Polinesi...

Es CampurSemangkuk es campur dengan irisan nangka, cendol, dan mutiara tapioka dalam santan dan gula.SajianDessertTempat asalIndonesiaDaerahSecara nasional di Indonesia, juga populer di Asia TenggaraSuhu penyajianDinginBahan utamaEs serut, kelapa, berbagai buah, cincau, sirup, susu kental manisSunting kotak info • L • BBantuan penggunaan templat ini Media: Es Campur Es campur adalah salah satu minuman khas Indonesia, dibuat dengan mencampurkan berbagai jenis bahan dala...

Ancient Egyptian goddess of childbirth Part of a series onAncient Egyptian religion Beliefs Afterlife Cosmology Duat Ma'at Mythology Numerology Philosophy Soul Practices Funerals Offerings: Offering formula Temples Priestess of Hathor Pyramids Deities (list)Ogdoad Amun Amunet Hauhet Heh Kauket Kek Naunet Nu Ennead Atum Geb Isis Nephthys Nut Osiris Set Shu Tefnut A Aati Aker Akhty Amenhotep, son of Hapu Amesemi Ammit Am-heh Amu-Aa Anat Andjety Anhur Anput Anubis Anuket Apedemak Apep Apis Apt A...

Rob Blake is the current general manager of the Los Angeles Kings. The Los Angeles Kings are an American professional ice hockey team based in Los Angeles, California. They play in the Pacific Division of the Western Conference in the National Hockey League (NHL).[1] The team joined the NHL in 1967 as an expansion team with five other teams, and won their first Stanley Cup in 2012. Having first played at The Forum, the Kings have played their home games at the Staples Center since 19...

Halaman ini berisi artikel tentang kota. Untuk kabupaten bernama sama, lihat Kabupaten Bogor. Kota BogorKotaTranskripsi bahasa daerah • Aksara Sundaᮘᮧᮌᮧᮁ • Bahasa BelandaBuitenzorgDari atas : Istana Bogor, kiri ke kanan : Kota Bogor dan Gunung Salak, Kebun Raya Bogor BenderaLambangJulukan: Kota HujanMotto: Di nu kiwari ngancik nu bihari, seja ayeuna sampeureun jaga(Sunda) Segala hal di masa kini adalah pusaka masa silam, dan ikhtiar h...

Kesunanan Surakarta Hadiningratꦑꦱꦸꦤꦤꦤ꧀ꦯꦸꦫꦏꦂꦠꦲꦢꦶꦤꦶꦁꦫꦠ꧀Kasunanan Surakarta Hadiningrat1745–Sekarang Bendera Lambang(Sri Radya Laksana) Lagu kerajaan: Ladrang Sri Katon[1] Wilayah Kesunanan Surakarta sejak tahun 1830 (warna merah tua); termasuk berbagai daerah enklavenya serta wilayah Kadipaten Mangkunegaran (warna merah muda), yang merupakan wilayah vasal dari Kesunanan Surakarta.[2][3]Ibu kotaSurakartaBahasa resmiJaw...

Европейская сардина Научная классификация Домен:ЭукариотыЦарство:ЖивотныеПодцарство:ЭуметазоиБез ранга:Двусторонне-симметричныеБез ранга:ВторичноротыеТип:ХордовыеПодтип:ПозвоночныеИнфратип:ЧелюстноротыеГруппа:Костные рыбыКласс:Лучепёрые рыбыПодкласс:Новопёры...

«Promuovere, proteggere e garantire il pieno ed uguale godimento di tutti i diritti umani e di tutte le libertà fondamentali da parte delle persone con disabilità, e promuovere il rispetto per la loro intrinseca dignità. […]» (Art. 1 Convenzione delle Nazioni Unite sui diritti delle persone con disabilità dell'ONU, 13 dicembre 2006, CBM Swiss[1]) Uno sciatore con protesi Lo sci alpino paralimpico è la variante dello sci alpino praticata da atleti con disabilità fisiche o vi...

American diplomat (born 1967) Alexander LaskarisUnited States Ambassador to Chad IncumbentAssumed office August 18, 2022PresidentJoe BidenPreceded byGeeta PasiUnited States Ambassador to Guinea In officeAugust 3, 2012 – November 10, 2015PresidentBarack ObamaPreceded byPatricia MollerSucceeded byDennis B. Hankins Personal detailsBornAlexander Mark Laskaris1967 (age 56–57)Monterey, California, U.S.EducationGeorgetown University (BA)United States Army War College (MSS) ...

Branch of geometry Contact form redirects here. For web email forms, see Form (web) § Form-to-email scripts. The standard contact structure on R3. Each point in R3 has a plane associated to it by the contact structure, in this case as the kernel of the one-form dz − y dx. These planes appear to twist along the y-axis. It is not integrable, as can be verified by drawing an infinitesimal square in the x-y plane, and follow the path along the one-forms. The path would not return to the s...

1921 film by Rowland V. Lee Broken HeartsFilm posterDirected byRowland V. LeeWritten byEmilie Johnson (story)Joseph F. Poland (writer)Produced byHobart BosworthStarringHobart BosworthMadge BellamyRaymond McKeeCinematographyJ.O. TaylorDistributed byAssociated ProducersRelease date October 3, 1921 (1921-10-03) (U.S.) Running time6 reelsCountryUnited StatesLanguageSilent (English intertitles) Blind Hearts is a 1921 American silent drama film produced by Hobart Bosworth who sta...

2022 studio album by BlueHeart & SoulStudio album by BlueReleased28 October 2022 (2022-10-28)Length30:26LabelTag8BMGProducer Ben Collier Steve DuBerry Hugh Goldsmith Lewis Shay Jankel Ronny Svendsen Paul Visser Blue chronology Colours(2015) Heart & Soul(2022) Singles from Heart & Soul Haven't Found You YetReleased: 25 May 2022[1] Dance with MeReleased: 29 June 2022[1] MagneticReleased: 16 September 2022[2] Heart & SoulReleased: 4...

Sudah Pasti TahanSutradaraArizalProduserRaam SorayaPemeranWarkop DKI (Dono, Kasino, Indro)Sally MarcellinaNurul ArifinFortunellaAngel IbrahimPak TileLydia FebrianiTaufik SavalasPujiono Surya TrionoDistributorSoraya Intercine FilmsTanggal rilis19 Desember 1991Durasi... menitNegaraIndonesia Sudah Pasti Tahan adalah film drama komedi Indonesia yang dirilis dan diproduksi pada tanggal 19 Desember 1991 dengan disutradarai oleh Arizal dan dibintangi antara lain oleh Warkop DKI, Sally Marcellina, da...

منتخب قيرغيزستان لهوكي الجليد للناشئين البلد قرغيزستان ألوان الفريق رمز IIHF KGZ مشاركة دولية قيرغيزستان 12 – 4 الفلبين (كوالالمبور، ماليزيا؛ 13 ديسمبر 2017) أكبر فوز قيرغيزستان 13 – 2 الهند (كوالالمبور، ماليزيا؛ 17 ديسمبر 2017) قيرغيزستان 13 – 2 الفلبين ...
Road in South Australia This article needs additional citations for verification. Please help improve this article by adding citations to reliable sources. Unsourced material may be challenged and removed.Find sources: Strathalbyn Road – news · newspapers · books · scholar · JSTOR (June 2022) (Learn how and when to remove this message) Strathalbyn RoadSouth AustraliaNorthwest endSoutheast endCoordinates 35°00′55″S 138°44′11″E / ...

Pemukim Jepang di Kepulauan MarshallPresiden Amata KabuaPresiden Kessai NoteJumlah populasi70 (2007)[1][fn 1]Daerah dengan populasi signifikanJaluit, KwajaleinBahasaMarshall, Inggris, JepangAgamaProtestan;[2] Shinto dan BuddhaKelompok etnik terkaitMicronesians, Jepang, Okinawa Pemukiman Jepang di Kepulauan Marshall timbul dari perdagangan Jepang di wilayah Pasifik. Para penjelajah Jepang pertama datang ke Kepulauan Marshall pada akhir abad ke-19, meskipun pemukiman per...

Peta menunjukan lokasi Mercedes Mercedes adalah munisipalitas yang terletak di provinsi Camarines Norte, Filipina. Pada tahun 2015, munisipalitas ini memiliki populasi sebesar 50.841 jiwa atau. Pembagian wilayah Secara politis Mercedes terbagi menjadi 26 barangay, yaitu: Apuao Canimog Caringo Catandunganon Cayucyucan Colasi Del Rosario (Tagongtong) Gaboc Hamoraon Hinipaan Lalawigan Lanot Mambungalon Manguisoc Masalongsalong Matoogtoog Pambuhan Quinapaguian San Roque Tarum Sarana pendidikan Be...

新潟みなとトンネル 西詰・入船町側後方の建物は入船みなとタワー概要現況 供用中所属路線名 新潟港臨港道路入舟臨港線起点 新潟県新潟市中央区海辺町二番町終点 新潟県新潟市東区臨港町二丁目運用開通 2002年(平成14年)5月19日(暫定2車線)2005年(平成17年)7月24日(全面供用)管理 新潟県 新潟地域振興局新潟港湾事務所通行対象 自動車・自転車・歩行者通行料�...

加賀丸いも(かがまるいも)は、石川県能美市と小松市特産の伝統野菜。ヤマノイモ科ヤマノイモ属ナガイモ(Dioscorea polystachya)の中でも、ツクネイモ群と呼ばれる品種群の一種。 概要 加賀丸いも 能美市と小松市の一部という限られた地域で栽培される貴重な作物で、できのよいものはソフトボールのような大きさで丸い形が特徴である[1]。すりおろすと強い粘...

КоммунаЭскондоEscondeaux Герб 43°20′27″ с. ш. 0°07′50″ в. д.HGЯO Страна Франция Регион Юг — Пиренеи Департамент Верхние Пиренеи Кантон Рабастенс-де-Бигор Мэр Рене Рок(2014—2020) История и география Площадь 3,79 км² Высота центра 224–245 м Часовой пояс UTC+1:00, летом UTC+2:00 Населен...