Ш®Ш·ЩҲШ· Ш·ЩҠЩҒ Ш§Щ„ЩҮЩҠШҜШұЩҲШ¬ЩҠЩҶ
|
Read other articles:

US Supreme Court justice since 2022 (born 1970) Ketanji Brown JacksonOfficial portrait, 2022Associate Justice of the Supreme Court of the United StatesIncumbentAssumed office June 30, 2022Nominated byJoe BidenPreceded byStephen BreyerJudge of the United States Court of Appeals for the District of Columbia CircuitIn officeJune 17, 2021 вҖ“ June 29, 2022Nominated byJoe BidenPreceded byMerrick GarlandSucceeded byFlorence Y. PanJudge of the United States District Court for the Distri...

Ш§Щ„Ш№Щ„Ш§ЩӮШ§ШӘ Ш§Щ„ШЈЩҲШәЩҶШҜЩҠШ© Ш§Щ„ШіЩҠШұШ§Щ„ЩҠЩҲЩҶЩҠШ© ШЈЩҲШәЩҶШҜШ§ ШіЩҠШұШ§Щ„ЩҠЩҲЩҶ ШЈЩҲШәЩҶШҜШ§ ШіЩҠШұШ§Щ„ЩҠЩҲЩҶ ШӘШ№ШҜЩҠЩ„ Щ…ШөШҜШұЩҠ - ШӘШ№ШҜЩҠЩ„ Ш§Щ„Ш№Щ„Ш§ЩӮШ§ШӘ Ш§Щ„ШЈЩҲШәЩҶШҜЩҠШ© Ш§Щ„ШіЩҠШұШ§Щ„ЩҠЩҲЩҶЩҠШ© ЩҮЩҠ Ш§Щ„Ш№Щ„Ш§ЩӮШ§ШӘ Ш§Щ„Ш«ЩҶШ§ШҰЩҠШ© Ш§Щ„ШӘЩҠ ШӘШ¬Щ…Ш№ ШЁЩҠЩҶ ШЈЩҲШәЩҶШҜШ§ ЩҲШіЩҠШұШ§Щ„ЩҠЩҲЩҶ.[1][2][3][4][5] Щ…ЩӮШ§ШұЩҶШ© ШЁЩҠЩҶ Ш§Щ„ШЁЩ„ШҜЩҠЩҶ ЩҮШ°ЩҮ Щ…ЩӮШ§ШұЩҶШ© Ш№Ш§Щ…Ш© ЩҲЩ…ШұШ¬Ш№ЩҠШ© Щ„Щ„ШҜЩҲЩ„ШӘЩҠЩҶ:...

Ш§Щ„Ш№Щ„Ш§ЩӮШ§ШӘ Ш§Щ„ЩҠЩҲЩҶШ§ЩҶЩҠШ© Ш§Щ„ЩғЩҶШҜЩҠШ© Ш§Щ„ЩҠЩҲЩҶШ§ЩҶ ЩғЩҶШҜШ§ Ш§Щ„ЩҠЩҲЩҶШ§ЩҶ ЩғЩҶШҜШ§ ШӘШ№ШҜЩҠЩ„ Щ…ШөШҜШұЩҠ - ШӘШ№ШҜЩҠЩ„ Ш§Щ„Ш№Щ„Ш§ЩӮШ§ШӘ Ш§Щ„ЩҠЩҲЩҶШ§ЩҶЩҠШ© Ш§Щ„ЩғЩҶШҜЩҠШ© ЩҮЩҠ Ш§Щ„Ш№Щ„Ш§ЩӮШ§ШӘ Ш§Щ„Ш«ЩҶШ§ШҰЩҠШ© Ш§Щ„ШӘЩҠ ШӘШ¬Щ…Ш№ ШЁЩҠЩҶ Ш§Щ„ЩҠЩҲЩҶШ§ЩҶ ЩҲЩғЩҶШҜШ§.[1][2][3][4][5] Щ…ЩӮШ§ШұЩҶШ© ШЁЩҠЩҶ Ш§Щ„ШЁЩ„ШҜЩҠЩҶ ЩҮШ°ЩҮ Щ…ЩӮШ§ШұЩҶШ© Ш№Ш§Щ…Ш© ЩҲЩ…ШұШ¬Ш№ЩҠШ© Щ„Щ„ШҜЩҲЩ„ШӘЩҠЩҶ: ЩҲШ¬ЩҮ Ш§Щ„Щ…ЩӮШ§ШұЩҶШ© Ш§Щ„ЩҠЩҲЩҶШ§пҝҪ...

Surinamese football club Football clubBomastarFull nameSociaal Culturele Sportvereniging BomastarGroundunknownCapacity1,250LeagueEerste Klasse2015/1610th Home colours SCSV Bomastar, known as Bomastar is a Surinamese football club from Lelydorp that plays in the SVB Eerste Klasse, the second tier of Surinamese football. History Formerly known as HOB (House Of Billiards), SCSV Bomastar were born after the relegation of the former club from the SVB Hoofdklasse after the 2005вҖ“06 season.[1&#...

ЩҮШ°ЩҮ Ш§Щ„Щ…ЩӮШ§Щ„Ш© ШӘШӯШӘШ§Ш¬ Щ„Щ„Щ…ШІЩҠШҜ Щ…ЩҶ Ш§Щ„ЩҲШөЩ„Ш§ШӘ Щ„Щ„Щ…ЩӮШ§Щ„Ш§ШӘ Ш§Щ„ШЈШ®ШұЩү Щ„Щ„Щ…ШіШ§Ш№ШҜШ© ЩҒЩҠ ШӘШұШ§ШЁШ· Щ…ЩӮШ§Щ„Ш§ШӘ Ш§Щ„Щ…ЩҲШіЩҲШ№Ш©. ЩҒШ¶Щ„ЩӢШ§ ШіШ§Ш№ШҜ ЩҒЩҠ ШӘШӯШіЩҠЩҶ ЩҮШ°ЩҮ Ш§Щ„Щ…ЩӮШ§Щ„Ш© ШЁШҘШ¶Ш§ЩҒШ© ЩҲШөЩ„Ш§ШӘ ШҘЩ„Щү Ш§Щ„Щ…ЩӮШ§Щ„Ш§ШӘ Ш§Щ„Щ…ШӘШ№Щ„ЩӮШ© ШЁЩҮШ§ Ш§Щ„Щ…ЩҲШ¬ЩҲШҜШ© ЩҒЩҠ Ш§Щ„ЩҶШө Ш§Щ„ШӯШ§Щ„ЩҠ. (ШіШЁШӘЩ…ШЁШұ 2021) ЩҮШ°ЩҮ Ш§Щ„Щ…ЩӮШ§Щ„Ш© ЩҠШӘЩҠЩ…Ш© ШҘШ° ШӘШөЩ„ ШҘЩ„ЩҠЩҮШ§ Щ…ЩӮШ§Щ„Ш§ШӘ ШЈШ®ШұЩү ЩӮЩ„ЩҠЩ„Ш© Ш¬ШҜЩӢШ§. ЩҒШ¶Щ„ЩӢШ§ШҢ ШіШ§Ш№ШҜ ШЁШҘШ¶Ш§ЩҒШ© ЩҲШөЩ„Ш©...

SunriseMarkas besar di SuginamiNama asliж ӘејҸдјҡзӨҫгӮөгғігғ©гӮӨгӮәSebelumnyaNippon Sunrise Inc.ж ӘејҸдјҡзӨҫж—Ҙжң¬гӮөгғігғ©гӮӨгӮәJenisKabushiki gaisha (sebelumnya yЕ«gen gaisha)Industrianimasi Jepang dan perusahaan produksiDidirikanSeptember 1972; 51 tahun lalu (1972-09) (sebagai Sunrise Studio YK)November 1976; 47 tahun lalu (1976-11) (sebagai Nippon Sunrise; berganti nama Sunrise pada Juni 1987; 36 tahun lalu (1987-06))KantorpusatSuginami, TokyoTokohkunciMiyakawa Yasuo (Presi...

Election 2006 California's 50th congressional district special election ← 2004 June 6, 2006 November 2006 → Nominee Brian Bilbray Francine Busby Party Republican Democratic Popular vote 78,341 71,146 Percentage 49.30 44.77 Representative before election Duke Cunningham Republican Elected Representative Brian Bilbray Republican Elections in California Federal government U.S. President 1852 1856 1860 1864 1868 1872 1876 1880 1884 1888 1892 1896 1900 1904 1908 1...

American film director and screenwriter For other people with similar names, see Phil Kaufman (disambiguation). Philip KaufmanKaufman in 1991Born (1936-10-23) October 23, 1936 (age 87)Chicago, Illinois, U.S.Occupations Director screenwriter producer Years active1964вҖ“2012Spouse Rose Fisher (m. 1958; died 2009)Children1WebsitePhilipKaufman.com Philip Kaufman (born October 23, 1936) is an American film director and screenwriter who ...
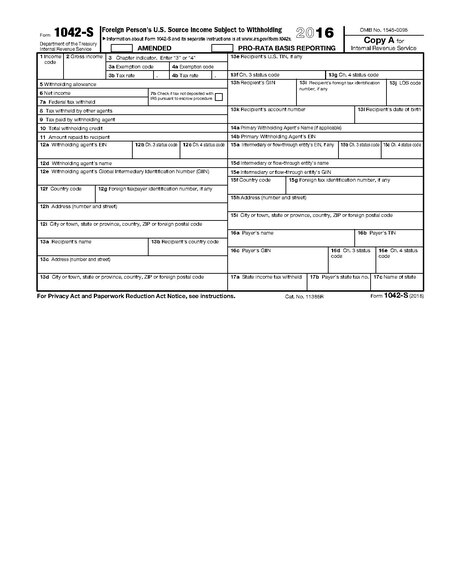
American tax forms Form 1042-S, 2016. Forms 1042, 1042-S and 1042-T are United States Internal Revenue Service tax forms dealing with payments to foreign persons, including nonresident aliens, foreign partnerships, foreign corporations, foreign estates, and foreign trusts.[1] Every withholding agent or intermediary, whether US or foreign, who has control, receipt, custody, disposal or payment of any fixed or determinable, annual or periodic US source income over foreign persons, must ...

Bhutan (dettagli) (dettagli) Bhutan - Localizzazione Dati amministrativiNome completoRegno del Bhutan Nome ufficialeаҪ аҪ–аҫІаҪҙаҪӮајӢаҪЎаҪҙаҪЈајӢDruk Yul Lingue ufficialidzongkha CapitaleThimphu (114551 ab. / 2017) PoliticaForma di governoMonarchia costituzionale ReJigme Khesar Namgyel Wangchuck Primo ministroTshering Tobgay Indipendenza1947 Ingresso nell'ONU21 settembre 1971 SuperficieTotale46.500 kmВІ (128Вә) % delle acque15% PopolazioneTotale771.612 ab. ...

Р”РөСҖжавРҪРёР№ РәРҫРјС–СӮРөСӮ СӮРөР»РөРұР°СҮРөРҪРҪСҸ С– СҖР°РҙС–РҫРјРҫРІР»РөРҪРҪСҸ РЈРәСҖаїРҪРё (Р”РөСҖР¶РәРҫРјСӮРөР»РөСҖР°РҙС–Рҫ) РҹСҖРёРјС–СүРөРҪРҪСҸ РәРҫРјС–СӮРөСӮСғЗагалСҢРҪР° С–РҪС„РҫСҖРјР°СҶС–СҸРҡСҖаїРҪР° РЈРәСҖаїРҪаДаСӮР° СҒСӮРІРҫСҖРөРҪРҪСҸ 2003РҡРөСҖС–РІРҪРө РІС–РҙРҫРјСҒСӮРІРҫ РҡР°РұС–РҪРөСӮ РңС–РҪС–СҒСӮСҖС–РІ РЈРәСҖаїРҪРёР С–СҮРҪРёР№ РұСҺРҙР¶РөСӮ 1 964 898 500 вӮҙ[1]Р“РҫР»РҫРІР° РһР»РөРі РқаливайРәРҫРҹС–РҙРІС–РҙРҫРјСҮС– РҫСҖ...

Rapid transit station in Philadelphia This article needs additional citations for verification. Please help improve this article by adding citations to reliable sources. Unsourced material may be challenged and removed.Find sources: EllsworthвҖ“Federal station вҖ“ news В· newspapers В· books В· scholar В· JSTOR (August 2022) (Learn how and when to remove this message) EllsworthвҖ“FederalEllsworthвҖ“Federal station platformGeneral informationLocation1200 Sout...

еңҹеә“жӣјж–ҜеқҰжҖ»з»ҹеңҹеә“жӣјж–ҜеқҰеӣҪеҫҪеңҹеә“жӣјж–ҜеқҰжҖ»з»ҹж——зҸҫд»»и°ўе°”иҫҫе°”В·еҲ«е°”еҫ·з©Ҷе“Ҳжў…еӨҡеӨ«иҮӘ2022е№ҙ3жңҲ19ж—Ҙе®ҳйӮёйҳҝд»Җе“Ҳе·ҙеҫ·жҖ»з»ҹеәңпјҲOguzkhan Presidential Palaceпјүж©ҹй—ңжүҖеңЁең°йҳҝд»Җе“Ҳе·ҙеҫ·д»»е‘ҪиҖ…зӣҙжҺҘйҖүдёҫд»»жңҹ7е№ҙпјҢеҸҜиҝһйҖүиҝһд»»йҰ–д»»иҗЁеё•е°”з©ҶжӢүзү№В·е°јдәҡдҪҗеӨ«и®ҫз«Ӣ1991е№ҙ10жңҲ27ж—Ҙ еңҹеә“жӣјж–ҜеқҰеңҹеә“жӣјж–ҜеқҰж”ҝеәңдёҺж”ҝжІ» еӣҪ家ж”ҝеәң еңҹеә“жӣјж–ҜеқҰе®Әжі• еӣҪж—— еӣҪеҫҪ еӣҪжӯҢ з«Ӣжі•ж©ҹй—ңпјҲиӢұиҜӯпјҡNational Council of Turkmenistanпјү ...
2020е№ҙеӨҸеӯЈеҘҘжһ—еҢ№е…ӢиҝҗеҠЁдјҡжіўе…°д»ЈиЎЁеңҳжіўе…°еӣҪж——IOCз·ЁзўјPOLNOCжіўиҳӯеҘ§жһ—еҢ№е…Ӣ委員жңғз¶Із«ҷolimpijski.plпјҲиӢұж–ҮпјүпјҲжіўе…°ж–Үпјү2020е№ҙеӨҸеӯЈеҘҘжһ—еҢ№е…ӢиҝҗеҠЁдјҡпјҲжқұдә¬пјү2021е№ҙ7жңҲ23ж—ҘиҮі8жңҲ8ж—ҘпјҲеҸ—2019еҶ зҠ¶з—…жҜ’з—…з–«жғ…еҪұе“ҚжҺЁиҝҹпјҢдҪҶд»Қдҝқз•ҷеҺҹе®ҡеҗҚз§°пјүйҒӢеӢ•е“Ў206еҸғиіҪй …зӣ®24дёӘеӨ§йЎ№ж——жүӢејҖ幕ејҸпјҡеё•з»ҙ尔·科зғӯе°јеҘҘеӨ«ж–ҜеҹәпјҲжёёжііпјүе’Ң马娅·жІғд»Җд№”еӨ«ж–ҜеҚЎпјҲиҮӘиЎҢиҪҰпјү[1]й—ӯ幕ејҸпјҡеҚЎзҪ—еҲ©еЁңВ·зәідәҡпјҲзҡ®еҲ’иүҮпјү&#...

Masa Demi MasaAlbum kompilasi karya ADA BandDirilis2013Direkam2003вҖ“2013GenrePop RockLabelUniversal Music IndonesiaBermudaKronologi ADA Band Empati (2011)Empati2011 Masa Demi Masa (2013) Chemistry (2016)Chemistry2016 Masa Demi Masa merupakan album kompilasi terbaik ketiga karya ADA Band yang dirilis pada tahun 2013. Album ini memuat 10 lagu, 3 di antaranya adalah lagu baru dan 7 lagu lainnya yang diambil dari album-album terdahulu bersama vokalis Donnie Sibarani, dengan hits mereka yang...

Euophrys kataokai Klasifikasi ilmiah Kerajaan: Animalia Filum: Arthropoda Kelas: Arachnida Ordo: Araneae Famili: Salticidae Genus: Euophrys Spesies: Euophrys kataokai Nama binomial Euophrys kataokaiIkeda, 1996 Euophrys kataokai adalah spesies laba-laba yang tergolong famili Salticidae. Spesies ini juga merupakan bagian dari genus Euophrys dan ordo Araneae. Nama ilmiah dari spesies ini pertama kali diterbitkan pada tahun 1996 oleh Ikeda. Laba-laba ini biasanya banyak ditemui di Rusia, Korea, ...

Гүquipe de Yougoslavie de football Г la Coupe du monde 1962 FГ©dГ©ration FГ©dГ©ration de Yougoslavie de football Classement 4e Organisateur(s) Chili Participation 5e Meilleure performance 4e en 1930 SГ©lectionneur Prvoslav MihajloviДҮ Capitaine Milan GaliДҮ Meilleur buteur DraЕҫan JerkoviДҮ (4) Гүquipe de Yougoslavie de football Г la Coupe du monde Coupe du monde 1958 Coupe du monde 1974 modifier L'Г©quipe de Yougoslavie de football est Г©liminГ©e en demi-finale de la Coupe du monde ...

See also: Sustainable landscaping A water collector at the EVA Lanxmeer housing development in Culemborg, Netherlands Sustainable gardening includes the more specific sustainable landscapes, sustainable landscape design, sustainable landscaping, sustainable landscape architecture, resulting in sustainable sites. It comprises a disparate group of horticultural interests that can share the aims and objectives associated with the international post-1980s sustainable development and sustainabili...

гӮ·гғігӮ¬гғқгғјгғ«и»ҚпјҲгӮ·гғігӮ¬гғқгғјгғ«гҒҗгӮ“гҖҖSingapore Armed Forces,SAFпјүгҒҜгӮ·гғігӮ¬гғқгғјгғ«гҒ«гҒҠгҒ‘гӮӢеӣҪйҳІзө„з№”гҖӮйҷёжө·з©әгҖҒгғҮгӮёгӮҝгғ«гғ»гӮӨгғігғҶгғӘгӮёгӮ§гғігӮ№гғ»гӮөгғјгғ“гӮ№гҒ®еӣӣи»ҚгҒӢгӮүгҒӘгӮҠгҖҒгӮ·гғігӮ¬гғқгғјгғ«зӢ¬з«ӢеҫҢгҒ®1965е№ҙгҒ«еүөиЁӯгҒ•гӮҢгҒҹгҖӮ жҰӮиҰҒ гӮ·гғігӮ¬гғқгғјгғ«гҒҜгҖҒе°ҸиҰҸжЁЎгҒӘеі¶еӣҪгҒ§гҒӮгӮҠгҒӘгҒҢгӮүгҖҒзөҢжёҲгҒҢеј·гҒ„гҒ“гҒЁгӮӮгҒӮгӮҠгҖҒе°ҸиҰҸжЁЎгҒӘгҒҢгӮүзІҫеј·гҒӘи»ҚгӮ’жңүгҒ—гҒҰгҒ„гӮӢгҖӮгӮ·гғігӮ¬гғқгғјгғ«и»ҚгҒҜгҖҒйҷёи»Қгғ»жө·и»Қгғ»з©әи»Қгғ»гғҮгӮёгӮҝгғ«...

1642 battle of the Franco-Spanish War Battle of HonnecourtPart of the Franco-Spanish War (1635вҖ“59) and the Thirty Years' WarThe Battle of Honnecourt, by Peter Snayers.[1] Perspective from the Spanish positions; note Abbey on left, and River Escaut directly behindDate26 May 1642LocationHonnecourt-sur-EscautResult Spanish victoryBelligerents Spain FranceCommanders and leaders Francisco de Melo Jean de Beck Conde de Bucquoy Marquis de Velada Comte de Guiche PuysГ©gur-Chaste...






