توزيع غاوسي غاما
|
Read other articles:

Eberhard August Wilhelm von ZimmermannBiografiKelahiran17 Agustus 1743 Uelzen Kematian4 Juli 1815 (71 tahun)Braunschweig Geheimrat (en) Data pribadiPendidikanUniversitas Georg August Göttingen Universitas Leiden Universitas Martin Luther Halle-Wittenberg KegiatanPekerjaanAhli geografi, zoologis, filsuf, dosen dan fisikawan Bekerja diTechnische Universität Braunschweig Karya kreatifSingkatan nama zoologiZimmermann Eberhard August Wilhelm von Zimmermann adalah seorang ahli g...

Artikel ini membutuhkan rujukan tambahan agar kualitasnya dapat dipastikan. Mohon bantu kami mengembangkan artikel ini dengan cara menambahkan rujukan ke sumber tepercaya. Pernyataan tak bersumber bisa saja dipertentangkan dan dihapus.Cari sumber: Barong Bali – berita · surat kabar · buku · cendekiawan · JSTOR Tiga genre tari tradisional di BaliWarisan Budaya Tak Benda UNESCOPertunjukan tari Barong dengan penari yang memegang kris dan Rangda di Bali.Ne...

Questa voce sull'argomento centri abitati del Rondônia è solo un abbozzo. Contribuisci a migliorarla secondo le convenzioni di Wikipedia. Espigão d'Oestecomune Espigão d'Oeste – Veduta LocalizzazioneStato Brasile Stato federato Rondônia MesoregioneLeste Rondoniense MicroregioneCacoal AmministrazioneSindacoCélio Renato da Silveira TerritorioCoordinate11°31′45″S 61°00′50″W / 11.529167°S 61.013889°W-11.529167; -61.013889 (Espigão d'Oeste)Coo...

Romanian actor Ovidiu Iuliu Moldovan (Romanian: [oˈvidju ˈjulju moldoˈvan]; January 1, 1942 – March 12, 2008) was a Romanian actor known for his work in Romanian film and television roles.[1] However, Moldovan focused almost exclusively on theater and stage roles during the later years of his career.[1] Moldovan was born on January 1, 1942, in Vișinelu, Mureș County. He was awarded the UNITER prize for his career achievements as a Romanian actor in 2004.[1&#...

Robin Drysdale Nazionalità Regno Unito Tennis Carriera Singolare1 Vittorie/sconfitte 35-78 Titoli vinti 0 Miglior ranking 71º (12 luglio 1978) Risultati nei tornei del Grande Slam Australian Open QF (1977) Roland Garros 1T (1977, 1978) Wimbledon 2T (1975, 1978) US Open 2T (1978) Doppio1 Vittorie/sconfitte 66-69 Titoli vinti 1 Miglior ranking 300º (2 gennaio 1984) Risultati nei tornei del Grande Slam Australian Open QF (1977) Roland Garros Wi...

Look up H, h, or aitch in Wiktionary, the free dictionary. H is the eighth letter of the Latin alphabet. H may also refer to: Musical symbols H number, Harry Halbreich reference mechanism for music by Honegger and Martinů H, B (musical note) H, B major People H. (noble) (died after 1279), an unidentified nobleman in the Kingdom of Hungary who served as master of the horse H. (1900–1995), British activist and economist Edgar Hardcastle H (born 1957), British guitarist Adrian Smith H (born ...

American gangster Michael The Pike Heitler (1876 – April 30, 1931) was a Prohibition gangster involved in prostitution for the Chicago Outfit. A Jewish mob boss born in what is today Ukraine, Heitler is buried at Waldheim Cemetery Co. in Forest Park, Illinois. Biography Heitler began operating brothels in Chicago during the early 1900s based out of west Madison Street. By 1911, he had become a leading crime figure and a top lieutenant to Chicago racketeer Jacob Mont Tennes, later driving ri...

Road in Los Angeles, California Obama BoulevardNamesakeBarack ObamaMaintained byLos Angeles Department of TransportationLength3.5 miles (5.6 km)LocationLos Angeles, CaliforniaWest endCulver City city limit near Ballona CreekEast endExposition Boulevard in Leimert Park, Los Angeles President Barack Obama Boulevard (commonly known as Obama Boulevard) is a major thoroughfare in South Los Angeles. It stretches 3.5 miles (5.6 km) from Baldwin Hills (past Baldwin Village and Cre...

Species of tree Grey box Eucalyptus microcarpa near Henty Scientific classification Kingdom: Plantae Clade: Tracheophytes Clade: Angiosperms Clade: Eudicots Clade: Rosids Order: Myrtales Family: Myrtaceae Genus: Eucalyptus Species: E. microcarpa Binomial name Eucalyptus microcarpa(Maiden) Maiden[1] Synonyms[1] Eucalyptus aff. odorata (W.Wimmera) Eucalyptus hemiphloia var. microcarpa Maiden Eucalyptus microcarpa 'Adelaide Variant' Flower buds and flowers Fruit Eucalyptus m...

Daily newspaper based in Argentina This article includes a list of general references, but it lacks sufficient corresponding inline citations. Please help to improve this article by introducing more precise citations. (December 2016) (Learn how and when to remove this message) La PrensaTypeDaily newspaperFormatBroadsheetOwner(s)Multimedios La CapitalPublisherMáximo GainzaFounded18 October 1869Political alignmentConservatism[1]HeadquartersBuenos Aires, ArgentinaCirculation100,000Websi...

Street in Manhattan, New York This article is about the street in Lower Manhattan. For the neighborhood commonly referred to as Wall Street, see Financial District, Manhattan. For the U.S. economy at large, for which Wall Street is commonly used as a metonym, see Economy of the United States. For other uses, see Wall Street (disambiguation). Wall StreetThe New York Stock Exchange Building's Broad Street entrance (right) as seen from Wall Street, April 2005. 23 Wall Street, the former headquar...

Battle of the First War of Scottish Independence Battle of Stirling BridgePart of the First War of Scottish IndependenceStirling Bridge seen by droneDate11 September 1297LocationStirling Bridge, Stirling, Scotland56°07′48″N 3°56′06″W / 56.130°N 3.935°W / 56.130; -3.935Result Scottish victoryBelligerents Scotland EnglandCommanders and leaders William WallaceAndrew de Moray (DOW) John de WarrenneHugh de Cressingham †Strength 5,300 to 6,300 men...

1933 U.S. Congress joint resolution to repeal the 18th Amendment and end Prohibition Joint Resolution Proposing the Twenty-First Amendment to the United States ConstitutionNicknamesBlaine ActEnacted bythe 72nd United States CongressEffectiveFebruary 20, 1933CodificationActs repealedEighteenth Amendment to the United States ConstitutionLegislative historyIntroduced in the Senate as S.J.Res. 211 by John J. Blaine (R-WI) on December 6, 1932Committee consideration by JudiciaryPassed the Sena...

American baseball player (born 1973) Baseball player Bob HowryHowry with the Chicago Cubs in 2007PitcherBorn: (1973-08-04) August 4, 1973 (age 50)Phoenix, Arizona, U.S.Batted: LeftThrew: RightMLB debutJune 21, 1998, for the Chicago White SoxLast MLB appearanceJuly 28, 2010, for the Chicago CubsMLB statisticsWin–loss record45–52Earned run average3.84Strikeouts653 Teams Chicago White Sox (1998–2002) Boston Red Sox (2002–2003) Cleveland Indians (2004–...

Species of butterfly Caltoris brunnea Figure 33 is Caltoris brunnea caere from Lionel de Nicéville's 1891 On New and Little-Known Butterflies from the Indo-Malayan Region Scientific classification Kingdom: Animalia Phylum: Arthropoda Class: Insecta Order: Lepidoptera Family: Hesperiidae Genus: Caltoris Species: C. brunnea Binomial name Caltoris brunnea(Snellen, 1876)[1] Synonyms Pamphila brunnea Snellen, 1876 Pamphila sodalis Mabille, 1893 Chapra caere de Nicéville, 1891 Caltor...

District in south east London, England This article is about a district in London. For the Scottish linguist and phonetician, see J. C. Catford. Human settlement in EnglandCatfordThe Catford Cat, a giant fibreglass sculpture of a black cat above the entrance to the Catford Centre, with the Village Green and Water Pump shown in the foregroundCatfordLocation within Greater LondonPopulation44,905 (2011 Census)[1]OS grid referenceTQ385735London boroughLewishamCeremonia...
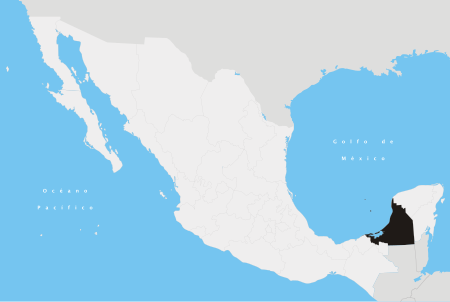
Calakmul adalah sebuah munisipalitas di negara bagian Campeche, Meksiko. Munisipalitas tersebut terletak di bagian tengah Semenanjung Yucatán. Sejarah dan geografi Munisipalitas (municipio) Calakmul berbatasan di bagian timur dengan Quintana Roo (munisipalitas José María Morelos, Bacalar, dan Othón P. Blanco) dan Belize (Distrik Orange Walk); di bagian selatan dengan Guatemala (Departemen Petén); dan di bagian utara dan barat dengan munisipalitas-munisipalitas lain di Campeche (Candelari...

Sporting event delegationIvory Coast at the2015 World Championships in AthleticsWA codeCIVin BeijingCompetitors4Medals Gold 0 Silver 0 Bronze 0 Total 0 World Championships in Athletics appearances19801983198719911993199519971999200120032005200720092011201320152017201920222023 Ivory Coast competed at the 2015 World Championships in Athletics in Beijing, China, from 22 to 30 August 2015.[1] Results (q – qualified, NM – no mark, SB – season best, w – wind assisted) Men Track and...

基本的な海域の区分。領海の幅は基線から12海里まで。 領海(りょうかい、英語: territorial sea、フランス語: eaux territoriales)とは、基線から最大12海里(約22.2キロメートル)までの範囲で国家が設定した帯状の水域であり、沿岸国の主権が及ぶ水域である(右図参照)[1][2][3]。沿岸海(えんがんかい)といわれることもある[1]。 領海、領海�...

Criminal offenses committed by the lower social classes This article has multiple issues. Please help improve it or discuss these issues on the talk page. (Learn how and when to remove these messages) This article possibly contains synthesis of material which does not verifiably mention or relate to the main topic. Relevant discussion may be found on the talk page. (September 2011) (Learn how and when to remove this message) This article is written like a personal reflection, personal essay, ...



















![{\displaystyle \pi (\mu ,\tau )\propto \tau ^{\alpha _{0}-{\frac {1}{2}}}\,\exp[-\beta _{0}\tau ]\,\exp \left[-{\frac {\lambda _{0}\tau (\mu -\mu _{0})^{2}}{2}}\right].}](https://wikimedia.org/api/rest_v1/media/math/render/svg/beb41e025bfbe7ea2f4087b48af2f9fb48b9c172)




![{\displaystyle {\begin{aligned}\mathbf {L} (\mathbf {X} \mid \tau ,\mu )&\propto \prod _{i=1}^{n}\tau ^{1/2}\exp \left[{\frac {-\tau }{2}}(x_{i}-\mu )^{2}\right]\\[5pt]&\propto \tau ^{n/2}\exp \left[{\frac {-\tau }{2}}\sum _{i=1}^{n}(x_{i}-\mu )^{2}\right]\\[5pt]&\propto \tau ^{n/2}\exp \left[{\frac {-\tau }{2}}\sum _{i=1}^{n}(x_{i}-{\bar {x}}+{\bar {x}}-\mu )^{2}\right]\\[5pt]&\propto \tau ^{n/2}\exp \left[{\frac {-\tau }{2}}\sum _{i=1}^{n}\left((x_{i}-{\bar {x}})^{2}+({\bar {x}}-\mu )^{2}\right)\right]\\[5pt]&\propto \tau ^{n/2}\exp \left[{\frac {-\tau }{2}}\left(ns+n({\bar {x}}-\mu )^{2}\right)\right],\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/2af15facc697809f43f699f3db0ff784f59dea45)


![{\displaystyle {\begin{aligned}\mathbf {P} (\tau ,\mu \mid \mathbf {X} )&\propto \mathbf {L} (\mathbf {X} \mid \tau ,\mu )\pi (\tau ,\mu )\\&\propto \tau ^{n/2}\exp \left[{\frac {-\tau }{2}}\left(ns+n({\bar {x}}-\mu )^{2}\right)\right]\tau ^{\alpha _{0}-{\frac {1}{2}}}\,\exp[{-\beta _{0}\tau }]\,\exp \left[-{\frac {\lambda _{0}\tau (\mu -\mu _{0})^{2}}{2}}\right]\\&\propto \tau ^{{\frac {n}{2}}+\alpha _{0}-{\frac {1}{2}}}\exp \left[-\tau \left({\frac {1}{2}}ns+\beta _{0}\right)\right]\exp \left[-{\frac {\tau }{2}}\left(\lambda _{0}(\mu -\mu _{0})^{2}+n({\bar {x}}-\mu )^{2}\right)\right]\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/de9c451b7469721ab4ef04a1df37564f2a9ad70b)

![{\displaystyle {\begin{aligned}\mathbf {P} (\tau ,\mu \mid \mathbf {X} )&\propto \tau ^{{\frac {n}{2}}+\alpha _{0}-{\frac {1}{2}}}\exp \left[-\tau \left({\frac {1}{2}}ns+\beta _{0}\right)\right]\exp \left[-{\frac {\tau }{2}}\left(\left(\lambda _{0}+n\right)\left(\mu -{\frac {\lambda _{0}\mu _{0}+n{\bar {x}}}{\lambda _{0}+n}}\right)^{2}+{\frac {\lambda _{0}n({\bar {x}}-\mu _{0})^{2}}{\lambda _{0}+n}}\right)\right]\\&\propto \tau ^{{\frac {n}{2}}+\alpha _{0}-{\frac {1}{2}}}\exp \left[-\tau \left({\frac {1}{2}}ns+\beta _{0}+{\frac {\lambda _{0}n({\bar {x}}-\mu _{0})^{2}}{2(\lambda _{0}+n)}}\right)\right]\exp \left[-{\frac {\tau }{2}}\left(\lambda _{0}+n\right)\left(\mu -{\frac {\lambda _{0}\mu _{0}+n{\bar {x}}}{\lambda _{0}+n}}\right)^{2}\right]\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/be3f6e839a36bd0b1ccaf4ed857d7389eb834b50)
