تآثر مغزلي مداري
|
Read other articles:

András 1222Dibuat1222PenulisAndrás II dari HungariaTujuanMemastikan hak-hak bangsawan Bulla Emas 1222 adalah sebuah bulla emas atau maklumat yang dikeluarkan oleh Raja András II dari Hungaria. Raja András II dipaksa oleh bangsawan-bangsawan di negaranya untuk menerima Bulla Emas (Aranybulla) ini, yang merupakan salah satu contoh pertama batas konstitusional terhadap kekuasaan seorang penguasa monarki di Eropa.[1] The Golden Bull was issued at the year 1222 diet of Fehérvár.[...

Questa voce o sezione sull'argomento stagioni delle società calcistiche italiane non cita le fonti necessarie o quelle presenti sono insufficienti. Puoi migliorare questa voce aggiungendo citazioni da fonti attendibili secondo le linee guida sull'uso delle fonti. Segui i suggerimenti del progetto di riferimento. Voce principale: Cagliari Calcio. Cagliari CalcioStagione 1980-1981 Sport calcio Squadra Cagliari Allenatore Mario Tiddia Presidente Mariano Delogu Serie A6º Coppa Italia...

U.S. presidential election in Maryland Main article: 1980 United States presidential election 1980 United States presidential election in Maryland ← 1976 November 4, 1980 1984 → Nominee Jimmy Carter Ronald Reagan John B. Anderson Party Democratic Republican Independent Home state Georgia California Illinois Running mate Walter Mondale George H. W. Bush Patrick Lucey Electoral vote 10 0 0 Popular vote 726,161 680,606 119,537 Percentage 47.12% 44...

2019 vampire film BitDirected byBrad Michael ElmoreWritten byBrad Michael ElmoreCinematographyCristina DunlapMusic byWolfmen of MarsDistributed byVertical EntertainmentRelease dates May 24, 2019 (2019-05-24) (Inside Out)[1] April 24, 2020 (2020-04-24)[2] Running time90 minutes Bit is a 2019 vampire film written and directed by Brad Michael Elmore.[2] The film stars Nicole Maines as Laurel, a girl who is turned into a vampire while spen...

Diagram ini menunjukkan orbit satelit iregular Saturnus. Di tengah, orbit Titan, sebuah satelit yang regular, ditandai dengan warna merah sebagai perbandingan. Kari (satelit) adalah satelit alami dari planet Saturnus. Saturnus memiliki 62 satelit, dengan 53 di antaranya telah dinamai dan hanya 13 di antaranya memiliki diameter lebih besar dari 50 kilometer. Referensi http://solarsystem.nasa.gov/planets/profile.cfm?Display=Sats&Object=Saturn Diarsipkan 2014-04-16 di Wayback Machine.

Real Madrid bermain melawan Fuenlabrada Liga ACB adalah sebuah divisi bola basket profesional teratas dari sistem liga bola basket Spanyol. Dikelola oleh Asociación de Clubs de Baloncesto (ACB), Liga ACB diperebutkan oleh 18 tim, dengan dua tim dengan posisi terendah degradasi ke LEB Oro dan digantikan oleh tim top di divisi itu ditambah pemenang play-off. Kompetisi ini didirikan sebagai ACB Primera División pada tahun 1983 setelah keputusan klub di Liga Nacional, didirikan pada tahun 1957,...

Puntarenas Ciudad de PuntarenasJulukan: La perla del Pacífico, El PuertoNegaraKosta RikaProvinsiPuntarenasCantonPuntarenasPemerintahan • Wali kotaAgnes Gomez FranceschiLuas • Total10 km2 (4 sq mi) • Luas daratan30 km2 (10 sq mi) • Luas perairan60 km2 (25 sq mi)Ketinggian5 m (16 ft)Populasi (2000) • Total102.504Zona waktuUTC-6 (Central)Situs webhttp://www.munipuntarenas...

Filmmaking in Kuwait Cinema of KuwaitNo. of screens61 (2010)[1] • Per capita2.3 per 100,000 (2010)[1]Number of admissions (2008)[2]Total2,200,000Gross box office (2008)[2]Total$19.8 million Cinema in Kuwait was introduced in the mid-20th century. The dominance of American cinema posed a problem in the formation of Arab cinema in general and of Kuwaiti cinema in particular.[3] French film critic Guy Hennebelle argued that Arab ...

American professional wrestling and entertainment company World Wrestling Entertainment, LLCTrade nameWWEFormerlyTitan Sports, Inc. (1980–1999)World Wrestling Federation Entertainment, Inc. (1999–2002)World Wrestling Entertainment, Inc. (2002–2023)Company typeSubsidiaryIndustryProfessional wrestlingStreaming mediaPredecessorCapitol Wrestling Corporation Ltd.Founded January 1953; 71 years ago (1953-01)(as Capitol Wrestling Corporation Ltd.) April 1963; ...

Campeonato de Portugal 1935Campeonato de Portugal 1935 Competizione Taça de Portugal Sport Calcio Edizione 14ª Luogo Portogallo Sede finale Stadio do Lumiar Risultati Vincitore Benfica(3º titolo) Secondo Sporting Lisbona Semi-finalisti Porto Carcavelinhos FC Statistiche Incontri disputati 28 Gol segnati 133 (4,75 per incontro) Cronologia della competizione 1934 1936 Manuale Il Campeonato de Portugal 1935 fu la quattordicesima edizione del Campeonato de Po...

Travis Hampton Willingham Travis Hampton Willingham (Dallas, 3 agosto 1981) è un doppiatore statunitense. Indice 1 Biografia 2 Vita privata 3 Note 4 Altri progetti 5 Collegamenti esterni Biografia Nato a Dallas, si interessa alla recitazione fin da piccolo, iniziando a studiare presso la scuola privata J.R. Long Middle School. Si è laureato alla Woodrow Wilson High School[1][2] e ha studiato alla Texas Christian University. Nei primi anni 2000 si trasferisce a Los Angeles pe...

The South Korean honors system includes orders of merit, medals of honor, and commendations conferred by the South Korean government onto its citizens and foreigners. Orders Orders (Korean: 훈장; Hanja: 勳章) are given by the president of South Korea to people who rendered distinguished services to the country. The first honor, the Grand Order of Mugunghwa, was established in 1949.[1][2] Grand Order of Mugunghwa Order of Merit for National Foundation ...

خادم الحرمين الشريفين الملك عبد الله بن عبد العزيز آل سعود ملك المملكة العربية السعودية السادس الحاكم التاسع عشر من آل سعود العلم الملكي فترة الحكم1 أغسطس 2005 - 23 يناير 2015 ولي العهد سلطان بن عبد العزيز آل سعود (2005 - 2011) نايف بن عبد العزيز آل سعود (2011 - 2012) سلمان بن عبد العزيز آل س�...

SvenTokoh FrozenPenampilanperdanaFrozen (2013)PenciptaChris BuckJennifer LeePemeranAndrew Pirozzi(Frozen — musikal)Pengisi suaraFrank Welker(efek suara)InformasiSpesiesReindeerJenis kelaminLaki-lakiPekerjaanHewan peliharaan KristoffKeluargaKristoff (pemilik)Trolls (keluarga angkat) Sven adalah sebuah karakter fiksi yang muncul dalam film animasi Frozen (2013) yang diproduksi oleh Walt Disney Animation Studios. Ia adalah hewan peliharaan milik Kristoff. Sven, bersama dengan Kristoff, membant...

Multi-use indoor arena in Saskatoon, Saskatchewan SaskTel CentreSaskTel CentreLocation within SaskatchewanShow map of SaskatchewanSaskTel CentreLocation within CanadaShow map of CanadaFormer namesSaskatchewan Place (1988–2004)Credit Union Centre (2004–2014)Address3315 Thatcher AvenueSaskatoon, SaskatchewanS7R 1C4Coordinates52°11′20″N 106°40′44″W / 52.189°N 106.679°W / 52.189; -106.679OwnerCity of SaskatoonExecutive suites51Capacity15,100[1]Lacro...

For the FIM MotoE World Cup scheduled for 2019, see MotoE World Cup. FIM eRoadRacing World CupCategoryelectric motorcycleCountryInternationalFolded2013Last Riders' championHo Chi Fung (Europe) Eric Bostrom (N. America)Official websiteeRoadRacing.com The FIM eRoad Racing World Cup was a championship of electric motorcycle road racing, organised by the Fédération Internationale de Motocyclisme (FIM) and was only held in this form in 2013. It followed the unification of the former TTXGP series...

1992 United States Senate election in Alaska ← 1986 November 3, 1992 1998 → Nominee Frank Murkowski Tony Smith Mary Jordan Party Republican Democratic Green Popular vote 127,163 92,065 20,019 Percentage 53.05% 38.41% 8.35% Results by state house districtMurkowski: 40–50% 50–60%Smith: 40–50% 50–60% U.S. senator before election Frank ...
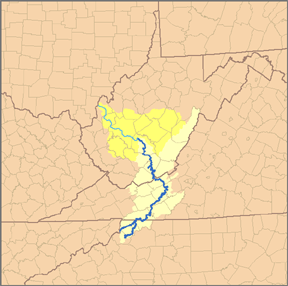
River in the Eastern United States New RiverThe New River within the New River Gorge as viewed from Hawks Nest State Park in West VirginiaMap of the Kanawha River watershed, with the New River (dark blue) and its watershed (light yellow) highlighted.LocationCountryUnited StatesStateNorth Carolina, Virginia, West VirginiaCountiesAshe NC, Alleghany NC, Watauga NC, Grayson VA, Carroll VA, Wythe VA, Pulaski VA, Montgomery VA, Giles VA, Mercer County, West Virginia, Summers County, West Virginia,...

DeltaDistrict BenderaLambang kebesaranMotto: Ours to preserve by hand and heart.Lokasi Delta di wilayah Greater Vancouver di British Columbia, KanadaNegara KanadaProvinsiBritish ColumbiaDistrikMetro VancouverBergabung1879Pemerintahan • MayorLois Jackson • Governing bodyDelta Municipal Council • MPsKerry-Lynne Findlay, Jinny Sims • MLAsGuy Gentner, Vicki HuntingtonLuas • Luas daratan183,70 km2 (7,090 sq mi)Ket...

UEA可以指: 東安格利亞大學(University of East Anglia) 國際世界語協會(Universala Esperanto Asocio) 这是一个消歧义页,羅列了有相同或相近的标题,但內容不同的条目。如果您是通过某條目的内部链接而转到本页,希望您能協助修正该處的内部链接,將它指向正确的条目。



