PIDжҺ§еҲ¶еҷЁпјҲжҜ”дҫӢ-з§ҜеҲҶ-еҫ®еҲҶжҺ§еҲ¶еҷЁпјүпјҢз”ұжҜ”дҫӢеҚ•е…ғпјҲProportionalпјүгҖҒз§ҜеҲҶеҚ•е…ғпјҲIntegralпјүе’Ңеҫ®еҲҶеҚ•е…ғпјҲDerivativeпјүз»„жҲҗ[1]гҖӮеҸҜд»ҘйҖҸйҒҺиӘҝж•ҙйҖҷдёүеҖӢе–®е…ғзҡ„еўһзӣҠ пјҢ
пјҢ е’Ң
е’Ң дҫҶиӘҝе®ҡе…¶зү№жҖ§гҖӮPIDжҺ§еҲ¶еҷЁдё»иҰҒйҖӮз”ЁдәҺеҹәжң¬дёҠзәҝжҖ§пјҢдё”еҠЁжҖҒзү№жҖ§дёҚйҡҸж—¶й—ҙеҸҳеҢ–зҡ„зі»з»ҹгҖӮ
дҫҶиӘҝе®ҡе…¶зү№жҖ§гҖӮPIDжҺ§еҲ¶еҷЁдё»иҰҒйҖӮз”ЁдәҺеҹәжң¬дёҠзәҝжҖ§пјҢдё”еҠЁжҖҒзү№жҖ§дёҚйҡҸж—¶й—ҙеҸҳеҢ–зҡ„зі»з»ҹгҖӮ
![]() PIDжҺ§еҲ¶еҷЁзҡ„ж–№еЎҠең–
PIDжҺ§еҲ¶еҷЁзҡ„ж–№еЎҠең–
PIDжҺ§еҲ¶еҷЁжҳҜдёҖдёӘеңЁе·ҘдёҡжҺ§еҲ¶еә”з”Ёдёӯеёёи§Ғзҡ„еӣһжҺҲеӣһи·ҜйғЁд»¶гҖӮиҝҷдёӘжҺ§еҲ¶еҷЁжҠҠ收йӣҶеҲ°зҡ„ж•°жҚ®е’ҢдёҖдёӘеҸӮиҖғеҖјиҝӣиЎҢжҜ”иҫғпјҢ然еҗҺжҠҠиҝҷдёӘе·®еҲ«з”ЁдәҺи®Ўз®—ж–°зҡ„иҫ“е…ҘеҖјпјҢиҝҷдёӘж–°зҡ„иҫ“е…ҘеҖјзҡ„зӣ®зҡ„жҳҜеҸҜд»Ҙи®©зі»з»ҹзҡ„ж•°жҚ®иҫҫеҲ°жҲ–иҖ…дҝқжҢҒеңЁеҸӮиҖғеҖјгҖӮPIDжҺ§еҲ¶еҷЁеҸҜд»Ҙж №жҚ®еҺҶеҸІж•°жҚ®е’Ңе·®еҲ«зҡ„еҮәзҺ°зҺҮжқҘи°ғж•ҙиҫ“е…ҘеҖјпјҢдҪҝзі»з»ҹжӣҙеҠ еҮҶзЎ®иҖҢзЁіе®ҡгҖӮ
PIDжҺ§еҲ¶еҷЁзҡ„жҜ”дҫӢеҚ•е…ғпјҲPпјүгҖҒз§ҜеҲҶеҚ•е…ғпјҲIпјүе’Ңеҫ®еҲҶеҚ•е…ғпјҲDпјүеҲҶеҲҘе°ҚжҮүзӣ®еүҚиӘӨе·®гҖҒйҒҺеҺ»зҙҜиЁҲиӘӨе·®еҸҠжңӘдҫҶиӘӨе·®гҖӮиӢҘжҳҜдёҚзҹҘйҒ“еҸ—жҺ§зі»зөұзҡ„зү№жҖ§пјҢдёҖиҲ¬иӘҚзӮәPIDжҺ§еҲ¶еҷЁжҳҜжңҖйҒ©з”Ёзҡ„жҺ§еҲ¶еҷЁ[2]гҖӮи—үз”ұиӘҝж•ҙPIDжҺ§еҲ¶еҷЁзҡ„дёүеҖӢеҸғж•ёпјҢеҸҜд»ҘиӘҝж•ҙжҺ§еҲ¶зі»зөұпјҢиЁӯжі•ж»ҝи¶іиЁӯиЁҲйңҖжұӮгҖӮжҺ§еҲ¶еҷЁзҡ„йҹҝжҮүеҸҜд»Ҙз”ЁжҺ§еҲ¶еҷЁе°ҚиӘӨе·®зҡ„еҸҚжҮүеҝ«ж…ўгҖҒжҺ§еҲ¶еҷЁйҒҺиЎқзҡ„зЁӢеәҰеҸҠзі»зөұйңҮзӣӘзҡ„зЁӢеәҰдҫҶиЎЁзӨәгҖӮдёҚйҒҺдҪҝз”ЁPIDжҺ§еҲ¶еҷЁдёҚдёҖе®ҡдҝқиӯүеҸҜйҒ”еҲ°зі»зөұзҡ„жңҖдҪіжҺ§еҲ¶пјҢд№ҹдёҚдҝқиӯүзі»зөұз©©е®ҡжҖ§гҖӮ
жңүдәӣжҮүз”ЁеҸӘйңҖиҰҒPIDжҺ§еҲ¶еҷЁзҡ„йғЁд»Ҫе–®е…ғпјҢеҸҜд»Ҙе°ҮдёҚйңҖиҰҒе–®е…ғзҡ„еҸғж•ёиЁӯзӮәйӣ¶еҚіеҸҜгҖӮеӣ жӯӨPIDжҺ§еҲ¶еҷЁеҸҜд»Ҙи®ҠжҲҗPIжҺ§еҲ¶еҷЁгҖҒPDжҺ§еҲ¶еҷЁгҖҒPжҺ§еҲ¶еҷЁжҲ–IжҺ§еҲ¶еҷЁгҖӮе…¶дёӯеҸҲд»ҘPIжҺ§еҲ¶еҷЁжҜ”ијғеёёз”ЁпјҢеӣ зӮәDжҺ§еҲ¶еҷЁе°ҚеӣһжҺҲйӣңиЁҠеҚҒеҲҶж•Ҹж„ҹпјҢиҖҢиӢҘжІ’жңүIжҺ§еҲ¶еҷЁзҡ„и©ұпјҢзі»зөұдёҚжңғеӣһеҲ°еҸғиҖғеҖјпјҢжңғеӯҳеңЁдёҖеҖӢиӘӨе·®йҮҸгҖӮ
еҸҚйҰҲеӣһи·ҜеҹәзЎҖ
PIDеӣһи·ҜжҳҜиҰҒиҮӘеҠЁе®һзҺ°дёҖдёӘж“ҚдҪңдәәе‘ҳз”ЁйҮҸе…·е’ҢжҺ§еҲ¶ж—Ӣй’®йҖІиЎҢзҡ„е·ҘдҪңпјҢиҝҷдёӘж“ҚдҪңдәәе‘ҳдјҡз”ЁйҮҸе…·жөӢзі»з»ҹиҫ“еҮәзҡ„з»“жһңпјҢ然еҗҺз”ЁжҺ§еҲ¶ж—Ӣй’®жқҘи°ғж•ҙиҝҷдёӘзі»з»ҹзҡ„иҫ“е…ҘпјҢзӣҙеҲ°зі»з»ҹзҡ„иҫ“еҮәеңЁйҮҸе…·дёҠжҳҫзӨәзЁіе®ҡзҡ„йңҖжұӮзҡ„з»“жһңпјҢеңЁж—§зҡ„жҺ§еҲ¶ж–ҮжЎЈйҮҢпјҢиҝҷдёӘиҝҮзЁӢеҸ«еҒҡвҖңеӨҚдҪҚвҖқиЎҢдёәпјҢйҮҸе…·иў«з§°дёәвҖңжөӢйҮҸвҖқпјҢйңҖиҰҒзҡ„з»“жһңиў«з§°дёәвҖңиЁӯе®ҡеҖјвҖқиҖҢиЁӯе®ҡеҖје’ҢжөӢйҮҸд№Ӣй—ҙзҡ„е·®еҲ«иў«з§°дёәвҖңиҜҜе·®вҖқгҖӮ
дёҖдёӘжҺ§еҲ¶еӣһи·ҜеҢ…жӢ¬дёүдёӘйғЁеҲҶпјҡ
- зі»з»ҹзҡ„дј ж„ҹеҷЁеҫ—еҲ°зҡ„жөӢйҮҸз»“жһң
- жҺ§еҲ¶еҷЁдҪңеҮәеҶіе®ҡ
- йҖҡиҝҮдёҖдёӘиҫ“еҮәи®ҫеӨҮжқҘдҪңеҮәеҸҚеә”
жҺ§еҲ¶еҷЁд»Һдј ж„ҹеҷЁеҫ—еҲ°жөӢйҮҸз»“жһңпјҢ然еҗҺз”ЁйңҖжұӮз»“жһңеҮҸеҺ»жөӢйҮҸз»“жһңжқҘеҫ—еҲ°иҜҜе·®гҖӮ然еҗҺз”ЁиҜҜе·®жқҘи®Ўз®—еҮәдёҖдёӘеҜ№зі»з»ҹзҡ„зә жӯЈеҖјжқҘдҪңдёәиҫ“е…Ҙз»“жһңпјҢиҝҷж ·зі»з»ҹе°ұеҸҜд»Ҙд»Һе®ғзҡ„иҫ“еҮәз»“жһңдёӯж¶ҲйҷӨиҜҜе·®гҖӮ
еңЁдёҖдёӘPIDеӣһи·ҜдёӯпјҢиҝҷдёӘзә жӯЈеҖјжңүдёүз§Қз®—жі•пјҢж¶ҲйҷӨзӣ®еүҚзҡ„иҜҜе·®пјҢе№іеқҮиҝҮеҺ»зҡ„иҜҜе·®пјҢе’ҢйҖҸйҒҺиҜҜе·®зҡ„ж”№еҸҳжқҘйў„жөӢе°ҶжқҘзҡ„иҜҜе·®гҖӮ
жҜ”еҰӮиҜҙпјҢеҒҮеҰӮеҲ©з”Ёж°ҙз®ұеңЁдёәжӨҚзү©жҸҗдҫӣж°ҙпјҢж°ҙз®ұзҡ„ж°ҙйңҖиҰҒдҝқжҢҒеңЁдёҖе®ҡзҡ„й«ҳеәҰгҖӮеҸҜд»Ҙз”Ёдј ж„ҹеҷЁжқҘжЈҖжҹҘж°ҙз®ұйҮҢж°ҙзҡ„й«ҳеәҰпјҢиҝҷж ·е°ұеҫ—еҲ°дәҶжөӢйҮҸз»“жһңгҖӮжҺ§еҲ¶еҷЁдјҡжңүдёҖдёӘеӣәе®ҡзҡ„з”ЁжҲ·иҫ“е…ҘеҖјжқҘиЎЁзӨәж°ҙз®ұйңҖиҰҒзҡ„ж°ҙйқўй«ҳеәҰпјҢеҒҮи®ҫиҝҷдёӘеҖјжҳҜдҝқжҢҒ65пј…зҡ„ж°ҙйҮҸгҖӮжҺ§еҲ¶еҷЁзҡ„иҫ“еҮәи®ҫеӨҮдјҡиҝһеңЁз”ұ马иҫҫжҺ§еҲ¶зҡ„ж°ҙйҳҖй—ЁдёҠгҖӮжү“ејҖйҳҖй—Ёе°ұдјҡз»ҷж°ҙз®ұжіЁж°ҙпјҢе…ідёҠйҳҖй—Ёе°ұдјҡи®©ж°ҙз®ұйҮҢзҡ„ж°ҙйҮҸдёӢйҷҚгҖӮиҝҷдёӘйҳҖй—Ёзҡ„жҺ§еҲ¶дҝЎеҸ·е°ұжҳҜжҺ§еҲ¶еҸҳйҮҸгҖӮ
PIDжҺ§еҲ¶еҷЁеҸҜд»Ҙз”ЁжқҘжҺ§еҲ¶д»»дҪ•еҸҜиў«жөӢйҮҸеҸҠеҸҜиў«жҺ§еҲ¶еҸҳйҮҸгҖӮжҜ”еҰӮпјҢе®ғеҸҜд»Ҙз”ЁжқҘжҺ§еҲ¶жё©еәҰгҖҒеҺӢејәгҖҒжөҒйҮҸгҖҒеҢ–еӯҰжҲҗеҲҶгҖҒйҖҹеәҰзӯүзӯүгҖӮжұҪиҪҰдёҠзҡ„е·ЎиҲӘе®ҡйҖҹеҠҹиғҪе°ұжҳҜдёҖдёӘдҫӢеӯҗгҖӮ
дёҖдәӣжҺ§еҲ¶зі»з»ҹжҠҠж•°дёӘPIDжҺ§еҲ¶еҷЁдёІиҒ”иө·жқҘпјҢжҲ–жҳҜиҝһжҲҗзҪ‘з»ңгҖӮиҝҷж ·зҡ„иҜқпјҢдёҖдёӘдё»жҺ§еҲ¶еҷЁеҸҜиғҪдјҡдёәе…¶д»–жҺ§еҲ¶иҫ“еҮәз»“жһңгҖӮдёҖдёӘеёёи§Ғзҡ„дҫӢеӯҗжҳҜ马иҫҫзҡ„жҺ§еҲ¶гҖӮжҺ§еҲ¶зі»зөұжңғйңҖиҰҒ马иҫҫжңүдёҖдёӘеҸ—жҺ§зҡ„йҖҹеәҰпјҢжңҖеҫҢеҒңеңЁдёҖдёӘзЎ®е®ҡзҡ„дҪҚзҪ®гҖӮеҸҜз”ұдёҖеҖӢеӯҗжҺ§еҲ¶еҷЁз”ЁжқҘз®ЎзҗҶйҖҹеәҰпјҢдҪҶжҳҜиҝҷдёӘеӯҗжҺ§еҲ¶еҷЁзҡ„йҖҹеәҰжҳҜз”ұжҺ§еҲ¶й©¬иҫҫдҪҚзҪ®зҡ„дё»жҺ§еҲ¶еҷЁжқҘз®ЎзҗҶзҡ„гҖӮ
иҝһеҗҲе’ҢдёІиҒ”жҺ§еҲ¶еңЁеҢ–еӯҰиҝҮзЁӢжҺ§еҲ¶зі»з»ҹдёӯзӣёз•¶еёёи§ҒгҖӮ
жӯ·еҸІеҸҠжҮүз”Ё
 PIDжҺ§еҲ¶зҗҶи«–жҳҜз”ұи§ҖеҜҹиҲөжүӢзҡ„еӢ•дҪңиҖҢдҫҶ
PIDжҺ§еҲ¶зҗҶи«–жҳҜз”ұи§ҖеҜҹиҲөжүӢзҡ„еӢ•дҪңиҖҢдҫҶ
PIDжҺ§еҲ¶еҷЁеҸҜд»ҘиҝҪжәҜеҲ°1890е№ҙд»Јзҡ„и°ғйҖҹеҷЁиЁӯиЁҲ[2][3]гҖӮPIDжҺ§еҲ¶еҷЁжҳҜеңЁиҲ№иҲ¶иҮӘеҠЁж“ҚдҪңзі»зөұдёӯжјёжјёзҷјеұ•гҖӮ1911е№ҙElmer Sperryй–Ӣзҷјзҡ„жҺ§еҲ¶еҷЁжҳҜжңҖж—©жңҹPIDеһӢжҺ§еҲ¶еҷЁзҡ„е…¶дёӯд№ӢдёҖ[4]пјҢиҖҢ第дёҖеҖӢзҷјиЎЁPIDжҺ§еҲ¶еҷЁзҗҶи«–еҲҶжһҗи«–ж–Үзҡ„жҳҜдҝ„иЈ”зҫҺеӣҪе·ҘзЁӢеё«е°јеҸӨжӢүж–ҜВ·зұіиҜәе°”ж–Ҝеҹә(Minorsky 1922)гҖӮзұіиҜәе°”ж–Ҝеҹә當жҷӮеңЁиЁӯиЁҲзҫҺеңӢжө·и»Қзҡ„иҮӘеҠЁж“ҚдҪңзі»зөұпјҢд»–зҡ„иЁӯиЁҲжҳҜеҹәж–је°ҚиҲөжүӢзҡ„и§ҖеҜҹпјҢжҺ§еҲ¶иҲ№иҲ¶дёҚеҸӘжҳҜдҫқзӣ®еүҚзҡ„иӘӨе·®пјҢд№ҹиҖғж…®йҒҺеҺ»зҡ„иӘӨе·®д»ҘеҸҠиӘӨе·®зҡ„и®ҠеҢ–и¶ЁеӢў[5]пјҢеҫҢдҫҶзұіиҜәе°”ж–Ҝеҹәд№ҹз”Ёж•ёеӯёзҡ„ж–№ејҸеҠ д»ҘжҺЁе°Һ[6]гҖӮд»–зҡ„зӣ®зҡ„жҳҜеңЁж–јз©©е®ҡжҖ§пјҢиҖҢдёҚжҳҜжіӣз”Ёзҡ„жҺ§еҲ¶пјҢеӣ жӯӨеӨ§е№…зҡ„з°ЎеҢ–дәҶе•ҸйЎҢгҖӮжҜ”дҫӢжҺ§еҲ¶еҸҜд»ҘеңЁе°Ҹзҡ„ж“ҫеӢ•дёӢжңүз©©е®ҡжҖ§пјҢдҪҶз„Ўжі•ж¶ҲйҷӨз©©ж…ӢиӘӨе·®пјҢеӣ жӯӨеҠ е…ҘдәҶз©ҚеҲҶй …пјҢеҫҢдҫҶд№ҹеҠ е…ҘдәҶеҫ®еҲҶй …гҖӮ
當жҷӮеңЁж–°еўЁиҘҝе“ҘиҷҹжҲ°иүҰдёҠйҖІиЎҢжё¬и©ҰпјҢеҲ©з”ЁжҺ§еҲ¶еҷЁжҺ§еҲ¶иҲөзҡ„и§’йҖҹеәҰпјҢеҲ©з”ЁPIжҺ§еҲ¶еҷЁеҸҜд»Ҙи§’еәҰиӘӨе·®з¶ӯжҢҒеңЁВұ2В°д»Ҙе…§пјҢиӢҘеҠ дёҠDжҺ§еҲ¶пјҢи§’еәҰиӘӨе·®з¶ӯжҢҒеңЁВұ1/6В°пјҢжҜ”жңҖеҘҪзҡ„иҲөжүӢйӮ„иҰҒеҘҪ[7]гҖӮ
дёҚйҒҺеӣ зӮәжө·и»Қдәәе“Ўзҡ„жҠ—жӢ’пјҢжө·и»ҚйӮЈжҷӮеҖҷжңӘдҪҝз”ЁйҖҷеҘ—зі»зөұпјҢеңЁ1930е№ҙд»Јд№ҹжңүе…¶д»–дәәдҪңеҮәйЎһдјјзҡ„з ”з©¶гҖӮ
еңЁиҮӘеӢ•жҺ§еҲ¶зҷјеұ•зҡ„ж—©жңҹпјҢз”Ёж©ҹжў°иЁӯеӮҷдҫҶеҜҰзҸҫPIDжҺ§еҲ¶пјҢжҳҜз”ұ槓жЎҝгҖҒеҪҲз°§гҖҒйҳ»е°јеҸҠиіӘйҮҸзө„жҲҗпјҢеӨҡеҚҠжңғз”ЁеЈ“зё®ж°Јй«”й©…еӢ•гҖӮж°ЈеӢ•жҺ§еҲ¶еҷЁйӮ„дёҖеәҰжҳҜе·ҘжҘӯдёҠзҡ„жЁҷжә–гҖӮ
йӣ»еӯҗзҡ„йЎһжҜ”жҺ§еҲ¶еҷЁеҸҜд»Ҙз”Ёйӣ»жҷ¶й«”гҖҒзңҹз©әз®ЎгҖҒйӣ»е®№еҷЁеҸҠйӣ»йҳ»еҷЁзө„жҲҗгҖӮиЁұеӨҡиӨҮйӣңзҡ„йӣ»еӯҗзі»зөұдёӯеёёжңғеҢ…жӢ¬PIDжҺ§еҲ¶пјҢдҫӢеҰӮзЈҒзўҹзҡ„и®ҖеҜ«й ӯе®ҡдҪҚгҖҒйӣ»жәҗдҫӣжҮүеҷЁзҡ„йӣ»жәҗжўқ件гҖҒз”ҡиҮіжҳҜзҸҫд»Јең°йңҮе„Җзҡ„йҒӢеӢ•еҒөжё¬з·ҡи·ҜгҖӮзҸҫд»Јйӣ»еӯҗжҺ§еҲ¶еҷЁе·ІеӨ§е№…зҡ„иў«йҖҷдәӣеҲ©з”Ёе–®жҷ¶зүҮжҲ–FPGAдҫҶеҜҰзҸҫзҡ„ж•ёдҪҚжҺ§еҲ¶еҷЁжүҖеҸ–д»ЈгҖӮ
зҸҫд»Је·ҘжҘӯдҪҝз”Ёзҡ„PIDжҺ§еҲ¶еҷЁеӨҡеҚҠжңғз”ЁPLCжҲ–жңүе®үиЈ…йқўжқҝзҡ„ж•ёдҪҚжҺ§еҲ¶еҷЁдҫҶеҜҰзҸҫгҖӮи»ҹй«”еҜҰзҸҫзҡ„еҘҪиҷ•жҳҜзӣёе°ҚдҪҺе»үпјҢй…ҚеҗҲPIDеҜҰзҸҫж–№ејҸиӘҝж•ҙзҡ„йқҲж•ҸеәҰеҫҲеӨ§гҖӮеңЁе·ҘжҘӯйҚӢзҲҗгҖҒеЎ‘иҶ е°„еҮәж©ҹжў°гҖҒзғ«йҮ‘жңәеҸҠеҢ…иЈқиЎҢжҘӯдёӯйғҪжңғз”ЁеҲ°PIDжҺ§еҲ¶гҖӮ
и®ҠеҢ–зҡ„йӣ»еЈ“ијёеҮәеҸҜд»Ҙз”ЁPWMдҫҶеҜҰзҸҫпјҢд№ҹе°ұжҳҜеӣәе®ҡйҖұжңҹпјҢдҫқиҰҒијёеҮәзҡ„йҮҸеҺ»иӘҝж•ҙйҖұжңҹдёӯијёеҮәй«ҳйӣ»дҪҚзҡ„жҷӮй–“гҖӮе°Қж–јж•ёдҪҚзі»зөұпјҢе…¶жҷӮй–“жҜ”дҫӢжңүеҸҜиғҪжҳҜйӣўж•Јзҡ„пјҢдҫӢеҰӮйҖұжңҹжҳҜдәҢз§’пјҢй«ҳйӣ»дҪҚжҷӮй–“иЁӯе®ҡе–®дҪҚзӮә0.1з§’пјҢиЎЁзӨәеҸҜд»ҘеҲҶзӮә20ж јпјҢзІҫеәҰ5%пјҢеӣ жӯӨеӯҳеңЁдёҖйҮҸеҢ–иӘӨе·®пјҢдҪҶеҸӘиҰҒжҷӮй–“и§ЈжһҗеәҰеӨ й«ҳпјҢе°ұжңғжңүдёҚйҢҜзҡ„ж•ҲжһңгҖӮ
зҗҶи®ә
PIDжҳҜд»Ҙе®ғзҡ„дёүз§Қзә жӯЈз®—жі•иҖҢе‘ҪеҗҚгҖӮеҸ—жҺ§и®Ҡж•ёжҳҜдёүз§Қз®—жі•пјҲжҜ”дҫӢгҖҒз©ҚеҲҶгҖҒеҫ®еҲҶпјүзӣёеҠ еҫҢзҡ„зөҗжһңпјҢеҚізӮәе…¶ијёеҮәпјҢе…¶ијёе…ҘзӮәиҜҜе·®еҖјпјҲиЁӯе®ҡеҖјжёӣеҺ»жөӢйҮҸеҖјеҫҢзҡ„зөҗжһңпјүжҲ–жҳҜз”ұиҜҜе·®еҖјиЎҚз”ҹзҡ„дҝЎиҷҹгҖӮиӢҘе®ҡзҫ© зӮәжҺ§еҲ¶ијёеҮәпјҢPIDжј”з®—жі•еҸҜд»Ҙз”ЁдёӢејҸиЎЁзӨәпјҡ
зӮәжҺ§еҲ¶ијёеҮәпјҢPIDжј”з®—жі•еҸҜд»Ҙз”ЁдёӢејҸиЎЁзӨәпјҡ

е…¶дёӯ
 пјҡжҜ”дҫӢеўһзӣҠпјҢжҳҜиӘҝйҒ©еҸғж•ё
пјҡжҜ”дҫӢеўһзӣҠпјҢжҳҜиӘҝйҒ©еҸғж•ё пјҡз©ҚеҲҶеўһзӣҠпјҢд№ҹжҳҜиӘҝйҒ©еҸғж•ё
пјҡз©ҚеҲҶеўһзӣҠпјҢд№ҹжҳҜиӘҝйҒ©еҸғж•ё пјҡеҫ®еҲҶеўһзӣҠпјҢд№ҹжҳҜиӘҝйҒ©еҸғж•ё
пјҡеҫ®еҲҶеўһзӣҠпјҢд№ҹжҳҜиӘҝйҒ©еҸғж•ё пјҡиӘӨе·®=иЁӯе®ҡеҖјпјҲSPпјү- еӣһжҺҲеҖјпјҲPVпјү
пјҡиӘӨе·®=иЁӯе®ҡеҖјпјҲSPпјү- еӣһжҺҲеҖјпјҲPVпјү пјҡзӣ®еүҚжҷӮй–“
пјҡзӣ®еүҚжҷӮй–“ пјҡз©ҚеҲҶи®Ҡж•ёпјҢж•ёеҖјеҫһ0еҲ°зӣ®еүҚжҷӮй–“
пјҡз©ҚеҲҶи®Ҡж•ёпјҢж•ёеҖјеҫһ0еҲ°зӣ®еүҚжҷӮй–“
з”Ёжӣҙдё“дёҡзҡ„иҜқжқҘи®ІпјҢPIDжҺ§еҲ¶еҷЁеҸҜд»ҘиҰ–зӮәжҳҜйў‘еҹҹзі»з»ҹзҡ„ж»ӨжіўеҷЁгҖӮеңЁи®Ўз®—жҺ§еҲ¶еҷЁжңҖз»ҲжҳҜеҗҰдјҡиҫҫеҲ°зЁіе®ҡз»“жһңж—¶пјҢжӯӨжҖ§иіӘеҫҲжңүз”ЁгҖӮеҰӮжһңж•°еҖјжҢ‘йҖүдёҚеҪ“пјҢжҺ§еҲ¶зі»з»ҹзҡ„иҫ“е…ҘеҖјдјҡеҸҚеӨҚжҢҜзӣӘпјҢиҝҷеҜјиҮҙзі»з»ҹеҸҜиғҪж°ёиҝңж— жі•иҫҫеҲ°йў„и®ҫеҖјгҖӮ
PIDжҺ§еҲ¶еҷЁзҡ„дёҖиҲ¬иҪ¬з§»еҮҪж•°жҳҜпјҡ
 ,
,
е…¶дёӯCжҳҜдёҖдёӘеҸ–еҶідәҺзі»з»ҹеёҰе®Ҫзҡ„еёёж•°гҖӮ
жҜ”дҫӢжҺ§еҲ¶й …
 дёҚеҗҢжҜ”дҫӢеўһзӣҠKpдёӢпјҢеҸ—жҺ§и®Ҡж•ёе°ҚжҷӮй–“зҡ„и®ҠеҢ–пјҲKiе’ҢKdз¶ӯжҢҒе®ҡеҖјпјү
дёҚеҗҢжҜ”дҫӢеўһзӣҠKpдёӢпјҢеҸ—жҺ§и®Ҡж•ёе°ҚжҷӮй–“зҡ„и®ҠеҢ–пјҲKiе’ҢKdз¶ӯжҢҒе®ҡеҖјпјү
жҜ”дҫӢжҺ§еҲ¶иҖғж…®еҪ“еүҚиӘӨе·®пјҢиҜҜе·®еҖје’ҢдёҖдёӘжӯЈеҖјзҡ„еёёж•°KpпјҲиЎЁзӨәжҜ”дҫӢпјүзӣёд№ҳгҖӮKpеҸӘжҳҜеңЁжҺ§еҲ¶еҷЁзҡ„иҫ“еҮәе’Ңзі»з»ҹзҡ„иҜҜе·®жҲҗжҜ”дҫӢзҡ„ж—¶еҖҷжҲҗз«ӢгҖӮжҜ”еҰӮиҜҙпјҢдёҖдёӘз”өзғӯеҷЁжҺ§еҲ¶еҷЁжҳҜеңЁзӣ®жЁҷжә«еәҰе’ҢеҜҰйҡӣжә«еәҰе·®10В°CжҷӮжңү100%зҡ„ијёеҮәпјҢиҖҢе…¶зӣ®жЁҷеҖјжҳҜ25В°CгҖӮйӮЈд№Ҳе®ғеңЁ15В°Cзҡ„ж—¶еҖҷдјҡиҫ“еҮә100%пјҢеңЁ20В°Cзҡ„ж—¶еҖҷдјҡиҫ“еҮә50%пјҢеңЁ24В°Cзҡ„ж—¶еҖҷиҫ“еҮә10пј…пјҢжіЁж„ҸеңЁиҜҜе·®жҳҜ0зҡ„ж—¶еҖҷпјҢжҺ§еҲ¶еҷЁзҡ„иҫ“еҮәд№ҹжҳҜ0гҖӮ
жҜ”дҫӢжҺ§еҲ¶зҡ„ијёеҮәеҰӮдёӢпјҡ

иӢҘжҜ”дҫӢеўһзӣҠеӨ§пјҢеңЁзӣёеҗҢиӘӨе·®йҮҸдёӢпјҢжңғжңүијғеӨ§зҡ„ијёеҮәпјҢдҪҶиӢҘжҜ”дҫӢеўһзӣҠеӨӘеӨ§пјҢжңғдҪҝзі»зөұдёҚз©©е®ҡгҖӮзӣёеҸҚзҡ„пјҢиӢҘжҜ”дҫӢеўһзӣҠе°ҸпјҢиӢҘеңЁзӣёеҗҢиӘӨе·®йҮҸдёӢпјҢе…¶ијёеҮәијғе°ҸпјҢеӣ жӯӨжҺ§еҲ¶еҷЁжңғијғдёҚж•Ҹж„ҹзҡ„гҖӮиӢҘжҜ”дҫӢеўһзӣҠеӨӘе°ҸпјҢ當жңүе№Іж“ҫеҮәзҸҫжҷӮпјҢе…¶жҺ§еҲ¶дҝЎиҷҹеҸҜиғҪдёҚеӨ еӨ§пјҢз„Ўжі•дҝ®жӯЈе№Іж“ҫзҡ„еҪұйҹҝгҖӮ
з©©ж…ӢиӘӨе·®
жҜ”дҫӢжҺ§еҲ¶еңЁиӘӨе·®зӮә0жҷӮпјҢе…¶ијёеҮәд№ҹжңғзӮә0гҖӮиӢҘиҰҒи®“еҸ—жҺ§ијёеҮәзӮәйқһйӣ¶зҡ„ж•ёеҖјпјҢе°ұйңҖиҰҒз”ўз”ҹдёҖеҖӢз©©ж…ӢиӘӨе·®жҲ–еҒҸ移йҮҸ[a]гҖӮ
з©ҚеҲҶжҺ§еҲ¶й …
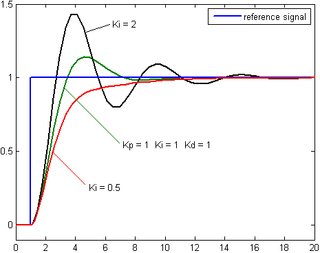 дёҚеҗҢз©ҚеҲҶеўһзӣҠKiдёӢпјҢеҸ—жҺ§и®Ҡж•ёе°ҚжҷӮй–“зҡ„и®ҠеҢ–пјҲKpе’ҢKdз¶ӯжҢҒе®ҡеҖјпјү
дёҚеҗҢз©ҚеҲҶеўһзӣҠKiдёӢпјҢеҸ—жҺ§и®Ҡж•ёе°ҚжҷӮй–“зҡ„и®ҠеҢ–пјҲKpе’ҢKdз¶ӯжҢҒе®ҡеҖјпјү
з§ҜеҲҶжҺ§еҲ¶иҖғж…®иҝҮеҺ»иӘӨе·®пјҢе°ҮиҜҜе·®еҖјиҝҮеҺ»дёҖж®өж—¶й—ҙе’ҢпјҲиҜҜе·®е’Ңпјүд№ҳд»ҘдёҖдёӘжӯЈеҖјзҡ„еёёж•°KiгҖӮKiд»ҺиҝҮеҺ»зҡ„е№іеқҮиҜҜе·®еҖјжқҘжүҫеҲ°зі»з»ҹзҡ„иҫ“еҮәз»“жһңе’Ңйў„е®ҡеҖјзҡ„е№іеқҮиҜҜе·®гҖӮдёҖдёӘз®ҖеҚ•зҡ„жҜ”дҫӢзі»з»ҹдјҡйңҮзӣӘпјҢдјҡеңЁйў„е®ҡеҖјзҡ„йҷ„иҝ‘жқҘеӣһеҸҳеҢ–пјҢеӣ дёәзі»з»ҹж— жі•ж¶ҲйҷӨеӨҡдҪҷзҡ„зә жӯЈгҖӮйҖҡиҝҮеҠ дёҠиҙҹзҡ„е№іеқҮиҜҜе·®еҖјпјҢе№іеқҮзі»з»ҹиҜҜе·®еҖје°ұдјҡжјёжјёеҮҸе°‘гҖӮжүҖд»ҘпјҢжңҖз»ҲиҝҷдёӘPIDеӣһи·Ҝзі»з»ҹдјҡеңЁиЁӯе®ҡеҖјзЁіе®ҡдёӢжқҘгҖӮ
з©ҚеҲҶжҺ§еҲ¶зҡ„ијёеҮәеҰӮдёӢпјҡ

з©ҚеҲҶжҺ§еҲ¶жңғеҠ йҖҹзі»зөұи¶Ёиҝ‘иЁӯе®ҡеҖјзҡ„йҒҺзЁӢпјҢдёҰдё”ж¶ҲйҷӨзҙ”жҜ”дҫӢжҺ§еҲ¶еҷЁжңғеҮәзҸҫзҡ„з©©ж…ӢиӘӨе·®гҖӮз©ҚеҲҶеўһзӣҠи¶ҠеӨ§пјҢи¶Ёиҝ‘иЁӯе®ҡеҖјзҡ„йҖҹеәҰи¶Ҡеҝ«пјҢдёҚйҒҺеӣ зӮәз©ҚеҲҶжҺ§еҲ¶жңғзҙҜиЁҲйҒҺеҺ»жүҖжңүзҡ„иӘӨе·®пјҢеҸҜиғҪжңғдҪҝеӣһжҺҲеҖјеҮәзҸҫйҒҺиЎқзҡ„жғ…еҪўгҖӮ
еҫ®еҲҶжҺ§еҲ¶й …
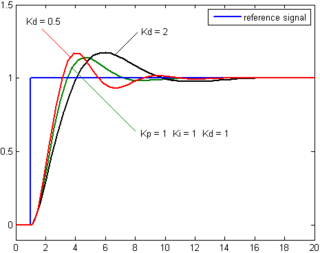 дёҚеҗҢеҫ®еҲҶеўһзӣҠKdдёӢпјҢеҸ—жҺ§и®Ҡж•ёе°ҚжҷӮй–“зҡ„и®ҠеҢ–пјҲKpе’ҢKiз¶ӯжҢҒе®ҡеҖјпјү
дёҚеҗҢеҫ®еҲҶеўһзӣҠKdдёӢпјҢеҸ—жҺ§и®Ҡж•ёе°ҚжҷӮй–“зҡ„и®ҠеҢ–пјҲKpе’ҢKiз¶ӯжҢҒе®ҡеҖјпјү
еҫ®еҲҶжҺ§еҲ¶иҖғж…®е°ҶжқҘиӘӨе·®пјҢи®Ўз®—иҜҜе·®зҡ„дёҖйҳ¶еҜјпјҢ并е’ҢдёҖдёӘжӯЈеҖјзҡ„еёёж•°Kdзӣёд№ҳгҖӮиҝҷдёӘеҜјж•°зҡ„жҺ§еҲ¶дјҡеҜ№зі»з»ҹзҡ„ж”№еҸҳдҪңеҮәеҸҚеә”гҖӮеҜјж•°зҡ„з»“жһңи¶ҠеӨ§пјҢйӮЈд№ҲжҺ§еҲ¶зі»з»ҹе°ұеҜ№иҫ“еҮәз»“жһңдҪңеҮәжӣҙеҝ«йҖҹзҡ„еҸҚеә”гҖӮиҝҷдёӘKdеҸӮж•°д№ҹжҳҜPIDиў«з§°дёәеҸҜйў„жөӢзҡ„жҺ§еҲ¶еҷЁзҡ„еҺҹеӣ гҖӮKdеҸӮж•°еҜ№еҮҸе°‘жҺ§еҲ¶еҷЁзҹӯжңҹзҡ„ж”№еҸҳеҫҲжңүеё®еҠ©гҖӮдёҖдәӣе®һйҷ…дёӯзҡ„йҖҹеәҰзј“ж…ўзҡ„зі»з»ҹеҸҜд»ҘдёҚйңҖиҰҒKdеҸӮж•°гҖӮ
еҫ®еҲҶжҺ§еҲ¶зҡ„ијёеҮәеҰӮдёӢпјҡ

еҫ®еҲҶжҺ§еҲ¶еҸҜд»ҘжҸҗжҳҮж•ҙе®ҡжҷӮй–“еҸҠзі»зөұз©©е®ҡжҖ§[8][9]гҖӮдёҚйҒҺеӣ зӮәзҙ”еҫ®еҲҶеҷЁдёҚжҳҜеӣ жһңзі»з»ҹпјҢеӣ жӯӨеңЁPIDзі»зөұеҜҰзҸҫжҷӮпјҢдёҖиҲ¬жңғзӮәеҫ®еҲҶжҺ§еҲ¶еҠ дёҠдёҖеҖӢдҪҺйҖҡжҝҫжіўеҷЁд»ҘйҷҗеҲ¶й«ҳй »еўһзӣҠеҸҠйӣңиЁҠ[10]гҖӮеҜҰйҷ…дёҠијғе°‘з”ЁеҲ°еҫ®еҲҶжҺ§еҲ¶пјҢдј°иЁҲPIDжҺ§еҲ¶еҷЁдёӯеҸӘжңүзҙ„20%жңүз”ЁеҲ°еҫ®еҲҶжҺ§еҲ¶[10]гҖӮ
еҸғж•ёиӘҝи©Ұ
PIDзҡ„еҸғж•ёиӘҝи©ҰжҳҜжҢҮйҖҸйҒҺиӘҝж•ҙжҺ§еҲ¶еҸғж•ёпјҲжҜ”дҫӢеўһзӣҠгҖҒз©ҚеҲҶеўһзӣҠ/жҷӮй–“гҖҒеҫ®еҲҶеўһзӣҠ/жҷӮй–“пјүи®“зі»зөұйҒ”еҲ°жңҖдҪізҡ„жҺ§еҲ¶ж•ҲжһңгҖӮз©©е®ҡжҖ§пјҲдёҚжңғжңүзҷјж•ЈжҖ§зҡ„йңҮзӣӘпјүжҳҜйҰ–иҰҒжўқ件пјҢжӯӨеӨ–пјҢдёҚеҗҢзі»зөұжңүдёҚеҗҢзҡ„иЎҢзӮәпјҢдёҚеҗҢзҡ„жҮүз”Ёе…¶йңҖжұӮд№ҹдёҚеҗҢпјҢиҖҢдё”йҖҷдәӣйңҖжұӮйӮ„еҸҜиғҪжңғдә’зӣёиЎқзӘҒгҖӮ
PIDеҸӘжңүдёүеҖӢеҸғж•ёпјҢеңЁеҺҹзҗҶдёҠе®№жҳ“иӘӘжҳҺпјҢдҪҶPIDеҸғж•ёиӘҝи©ҰжҳҜдёҖеҖӢеӣ°йӣЈзҡ„е·ҘдҪңпјҢеӣ зӮәиҰҒз¬ҰеҗҲдёҖдәӣзү№еҲҘзҡ„жә–еүҮпјҢиҖҢдё”PIDжҺ§еҲ¶жңүе…¶йҷҗеҲ¶еӯҳеңЁгҖӮжӯ·еҸІдёҠжңүиЁұеӨҡдёҚеҗҢзҡ„PIDеҸғж•ёиӘҝи©Ұж–№ејҸпјҢеҢ…жӢ¬йҪҠж јеӢ’пјҚ尼科зҲҫж–Ҝж–№жі•зӯүпјҢе…¶дёӯд№ҹжңүдёҖдәӣе·Із”іи«Ӣе°ҲеҲ©гҖӮ
PIDжҺ§еҲ¶еҷЁзҡ„иЁӯиЁҲеҸҠиӘҝи©ҰеңЁжҰӮеҝөдёҠеҫҲзӣҙиҰәпјҢдҪҶиӢҘжңүеӨҡеҖӢпјҲдё”дә’зӣёиЎқзӘҒпјүзҡ„зӣ®жЁҷпјҲдҫӢеҰӮй«ҳз©©е®ҡжҖ§еҸҠеҝ«йҖҹзҡ„жҡ«ж…ӢжҷӮй–“пјүйғҪиҰҒйҒ”еҲ°зҡ„и©ұпјҢеңЁеҜҰйҡӣдёҠеҫҲйӣЈе®ҢжҲҗгҖӮPIDжҺ§еҲ¶еҷЁзҡ„еҸғж•ёиӢҘд»”зҙ°зҡ„иӘҝи©ҰпјҢжңғжңүеҫҲеҘҪзҡ„ж•ҲжһңпјҢзӣёеҸҚзҡ„пјҢиӢҘиӘҝйҒ©дёҚ當пјҢж•ҲжһңжңғеҫҲе·®гҖӮдёҖиҲ¬еҲқе§ӢиЁӯиЁҲеёёйңҖиҰҒдёҚж–·зҡ„йӣ»и…Ұ模擬пјҢдёҰдё”дҝ®ж”№еҸғж•ёпјҢдёҖзӣҙйҒ”еҲ°зҗҶжғізҡ„жҖ§иғҪжҲ–жҳҜеҸҜжҺҘеҸ—зҡ„еҰҘеҚ”зӮәжӯўгҖӮ
жңүдәӣзі»зөұжңүйқһз·ҡжҖ§зҡ„зү№жҖ§пјҢиӢҘеңЁз„ЎијүдёӢиӘҝи©Ұзҡ„еҸғж•ёеҸҜиғҪз„Ўжі•еңЁж»ҝијүдёӢеӢ•дҪңпјҢеҸҜд»ҘеҲ©з”ЁеўһзӣҠиҰҸеҠғзҡ„ж–№ејҸйҖІиЎҢдҝ®жӯЈпјҲеңЁдёҚеҗҢзҡ„жўқ件дёӢйҒёз”ЁдёҚеҗҢзҡ„ж•ёеҖјпјүгҖӮ
з©©е®ҡжҖ§
иӢҘPIDжҺ§еҲ¶еҷЁзҡ„еҸғж•ёжңӘжҢ‘йҒёеҰҘ當пјҢе…¶жҺ§еҲ¶еҷЁијёеҮәеҸҜиғҪжҳҜдёҚз©©е®ҡзҡ„пјҢд№ҹе°ұжҳҜе…¶ијёеҮәзҷјж•ЈпјҢйҒҺзЁӢдёӯеҸҜиғҪжңүйңҮзӣӘпјҢд№ҹеҸҜиғҪжІ’жңүйңҮзӣӘпјҢдё”е…¶ијёеҮәеҸӘеҸ—йЈҪе’ҢжҲ–жҳҜж©ҹжў°жҗҚеЈһзӯүеҺҹеӣ жүҖйҷҗеҲ¶гҖӮдёҚз©©е®ҡдёҖиҲ¬жҳҜеӣ зӮәйҒҺеӨ§еўһзӣҠйҖ жҲҗпјҢзү№еҲҘжҳҜйҮқе°Қ延йҒІжҷӮй–“еҫҲй•·зҡ„зі»зөұгҖӮ
дёҖиҲ¬иҖҢиЁҖпјҢPIDжҺ§еҲ¶еҷЁжңғиҰҒжұӮйҹҝжҮүзҡ„з©©е®ҡпјҢдёҚи«–зЁӢеәҸжўқ件еҸҠиЁӯе®ҡеҖјеҰӮдҪ•зө„еҗҲпјҢйғҪдёҚиғҪеҮәзҸҫеӨ§е№…жҢҜзӣӘзҡ„жғ…еҪўпјҢдёҚйҒҺжңүжҷӮеҸҜд»ҘжҺҘеҸ—иҮЁз•Ңз©©е®ҡзҡ„жғ…еҪў[дҫҶжәҗи«ӢжұӮ]гҖӮ
жңҖдҪіжҖ§иғҪ
PIDжҺ§еҲ¶еҷЁзҡ„жңҖдҪіжҖ§иғҪеҸҜиғҪе’ҢйҮқе°ҚйҒҺзЁӢи®ҠеҢ–жҲ–жҳҜиЁӯе®ҡеҖји®ҠеҢ–жңүй—ңпјҢд№ҹжңғйҡЁжҮүз”ЁиҖҢдёҚеҗҢгҖӮ
е…©еҖӢеҹәжң¬зҡ„йңҖжұӮжҳҜиӘҝж•ҙиғҪеҠӣпјҲregulationпјҢе№Іж“ҫжӢ’зө•пјҢдҪҝзі»зөұз¶ӯжҢҒеңЁиЁӯе®ҡеҖјпјүеҸҠе‘Ҫд»ӨиҝҪйҡЁ пјҲиЁӯе®ҡеҖји®ҠеҢ–дёӢпјҢжҺ§еҲ¶еҷЁијёеҮәиҝҪйҡЁиЁӯе®ҡеҖјзҡ„еҸҚжҮүйҖҹеәҰпјүгҖӮжңүй—ңе‘Ҫд»ӨиҝҪйҡЁзҡ„дёҖдәӣжә–еүҮеҢ…жӢ¬жңүдёҠжҳҮжҷӮй–“еҸҠж•ҙе®ҡжҷӮй–“гҖӮжңүдәӣжҮүз”ЁеҸҜиғҪеӣ зӮәе®үе…ЁиҖғйҮҸпјҢдёҚе…ҒиЁұијёеҮәи¶…йҒҺиЁӯе®ҡеҖјпјҢд№ҹжңүдәӣжҮүз”ЁиҰҒжұӮеңЁеҲ°йҒ”иЁӯе®ҡеҖјйҒҺзЁӢдёӯзҡ„иғҪйҮҸеҸҜд»ҘжңҖе°ҸеҢ–гҖӮ
еҗ„ж–№жі•зҡ„з°Ўд»Ӣ
жңүиЁұеӨҡзЁ®иӘҝи©ҰPIDжҺ§еҲ¶еҷЁеҸғж•ёзҡ„ж–№жі•пјҢжңҖжңүж•Ҳзҡ„ж–№ејҸеӨҡеҚҠжҳҜе»әз«ӢжҹҗзЁ®зЁӢеәҸпјҢеҶҚдҫқдёҚеҗҢеҸғж•ёдёӢзҡ„еӢ•ж…Ӣзү№жҖ§дҫҶиӘҝи©ҰеҸғж•ёгҖӮзӣёе°ҚиҖҢиЁҖдәәе·ҘиӘҝи©Ұе…¶ж•ҲзҺҮијғе·®пјҢиӢҘжҳҜзі»зөұзҡ„йҹҝжҮүжҷӮй–“еҲ°ж•ёеҲҶйҗҳд»ҘдёҠпјҢжӣҙеҸҜд»ҘзңӢеҮәдәәе·ҘиӘҝи©Ұж•ҲзҺҮзҡ„дёҚдҪі[дҫҶжәҗи«ӢжұӮ]гҖӮ
иӘҝи©Ұж–№жі•зҡ„йҒёж“Үе’ҢжҳҜеҗҰеҸҜд»Ҙжҡ«жҷӮе°ҮжҺ§еҲ¶иҝҙи·ҜгҖҢйӣўз·ҡгҖҚжңүй—ңпјҢд№ҹе’Ңзі»зөұзҡ„йҹҝжҮүжҷӮй–“жңүй—ңгҖӮйӣўз·ҡжҳҜжҢҮдёҖеҖӢе’ҢеҜҰйҡӣдҪҝз”ЁжңүдәӣдёҚеҗҢзҡ„жўқ件пјҲдҫӢеҰӮдёҚеҠ иІ ијүпјүпјҢиҖҢдё”жҺ§еҲ¶еҷЁзҡ„ијёеҮәеҸӘйңҖиҖғж…®зҗҶи«–жғ…жіҒпјҢдёҚйңҖиҖғж…®еҜҰйҡӣжҮүз”ЁгҖӮеңЁз·ҡиӘҝи©ҰжҳҜеңЁеҜҰйҡӣжҮүз”Ёзҡ„жўқ件пјҢжҺ§еҲ¶еҷЁзҡ„ијёеҮәйңҖиҖғж…®еҜҰйҡӣзҡ„зі»зөұ
гҖӮиӢҘжҺ§еҲ¶иҝҙи·ҜеҸҜд»Ҙйӣўз·ҡпјҢжңҖеҘҪзҡ„иӘҝи©Ұж–№жі•жҳҜе°Қзі»зөұзөҰдёҖеҖӢжӯҘйҡҺијёе…ҘпјҢйҮҸжё¬е…¶ијёеҮәе°ҚжҷӮй–“зҡ„й—ңдҝӮпјҢеҶҚз”Ёе…¶йҹҝжҮүдҫҶжұәе®ҡеҸғж•ё[дҫҶжәҗи«ӢжұӮ]гҖӮ
йҒёж“ҮиӘҝи©Ұж–№ејҸ
| ж–№жі•
|
е„Әй»һ
|
зјәй»һ
|
| дәәе·ҘиӘҝи©Ұ
|
дёҚйңҖиҰҒж•ёеӯёпјҢеҸҜд»ҘеңЁз·ҡиӘҝи©Ұ
|
йңҖиҰҒжңү經驗зҡ„е·ҘзЁӢеё«[дҫҶжәҗи«ӢжұӮ]
|
| йҪҠж јеӢ’пјҚ尼科зҲҫж–Ҝж–№жі•
|
иў«иӯүеҜҰжңүж•Ҳзҡ„ж–№жі•пјҢеҸҜд»ҘеңЁз·ҡиӘҝи©Ұ
|
жңғеҪұйҹҝиЈҪзЁӢпјҢйңҖиҰҒи©ҰиӘӨпјҢеҫ—еҲ°зҡ„еҸғж•ёеҸҜиғҪдҪҝйҹҝжҮүеӨӘеҝ«[дҫҶжәҗи«ӢжұӮ]
|
| и»ҹй«”е·Ҙе…·
|
иӘҝйҒ©зҡ„дёҖиҮҙжҖ§пјҢеҸҜд»ҘеңЁз·ҡиӘҝи©ҰжҲ–йӣўз·ҡиӘҝи©ҰпјҢеҸҜд»Ҙй…ҚеҗҲи®Ўз®—жңәиҮӘеҠЁи®ҫи®ЎпјҢеҢ…жӢ¬й–ҘеҸҠж„ҹжё¬еҷЁзҡ„еҲҶжһҗпјҢеҸҜд»ҘеңЁдёӢијүеүҚйҖІиЎҢ模擬пјҢеҸҜд»Ҙж”ҜжҸҙйқһз©©ж…ӢпјҲNSSпјүзҡ„иӘҝи©Ұ
|
йңҖиҰҒжҲҗжң¬жҲ–жҳҜиЁ“з·ҙ[11]
|
| CohenвҖ“Coon
|
еҘҪзҡ„зЁӢеәҸжЁЎеһӢ
|
йңҖиҰҒдёҖдәӣж•ёеӯёпјҢйңҖйӣўз·ҡиӘҝи©ҰпјҢеҸӘе°ҚдёҖйҡҺзі»зөұжңүиүҜеҘҪж•Ҳжһң[дҫҶжәҗи«ӢжұӮ]
|
дәәе·ҘиӘҝж•ҙ
иӢҘйңҖеңЁзі»зөұд»ҚжңүиІ ијүзҡ„жғ…еҪўйҖІиЎҢиӘҝи©ҰпјҲз·ҡдёҠиӘҝи©ҰпјүпјҢжңүдёҖзЁ®дҪңжі•жҳҜе…Ҳе°Ү еҸҠ
еҸҠ иЁӯзӮәйӣ¶пјҢеўһеҠ
иЁӯзӮәйӣ¶пјҢеўһеҠ  дёҖзӣҙеҲ°иҝҙи·ҜијёеҮәйңҮзӣӘзӮәжӯўпјҢд№ӢеҫҢеҶҚе°Ү
дёҖзӣҙеҲ°иҝҙи·ҜијёеҮәйңҮзӣӘзӮәжӯўпјҢд№ӢеҫҢеҶҚе°Ү иЁӯе®ҡзӮәгҖҢ1/4жҢҜе№…иЎ°жёӣгҖҚпјҲдҪҝзі»зөұ第дәҢж¬ЎйҒҺиЎқйҮҸжҳҜ第дёҖж¬Ўзҡ„1/4пјүеўһзӣҠзҡ„дёҖеҚҠпјҢ然еҫҢеўһеҠ
иЁӯе®ҡзӮәгҖҢ1/4жҢҜе№…иЎ°жёӣгҖҚпјҲдҪҝзі»зөұ第дәҢж¬ЎйҒҺиЎқйҮҸжҳҜ第дёҖж¬Ўзҡ„1/4пјүеўһзӣҠзҡ„дёҖеҚҠпјҢ然еҫҢеўһеҠ  зӣҙеҲ°дёҖе®ҡжҷӮй–“еҫҢзҡ„з©©ж…ӢиӘӨе·®еҸҜиў«дҝ®жӯЈзӮәжӯўгҖӮдёҚйҒҺиӢҘ
зӣҙеҲ°дёҖе®ҡжҷӮй–“еҫҢзҡ„з©©ж…ӢиӘӨе·®еҸҜиў«дҝ®жӯЈзӮәжӯўгҖӮдёҚйҒҺиӢҘ еҸҜиғҪжңғйҖ жҲҗдёҚз©©е®ҡпјҢжңҖеҫҢиӢҘжңүйңҖиҰҒпјҢеҸҜд»ҘеўһеҠ
еҸҜиғҪжңғйҖ жҲҗдёҚз©©е®ҡпјҢжңҖеҫҢиӢҘжңүйңҖиҰҒпјҢеҸҜд»ҘеўһеҠ  пјҢдёҰзўәиӘҚеңЁиІ ијүи®ҠеӢ•еҫҢиҝҙи·ҜеҸҜд»ҘеӨ еҝ«зҡ„еӣһеҲ°е…¶иЁӯе®ҡеҖјпјҢдёҚйҒҺиӢҘ
пјҢдёҰзўәиӘҚеңЁиІ ијүи®ҠеӢ•еҫҢиҝҙи·ҜеҸҜд»ҘеӨ еҝ«зҡ„еӣһеҲ°е…¶иЁӯе®ҡеҖјпјҢдёҚйҒҺиӢҘ еӨӘеӨ§жңғйҖ жҲҗйҹҝжҮүеӨӘеҝ«еҸҠйҒҺиЎқгҖӮдёҖиҲ¬иҖҢиЁҖеҝ«йҖҹеҸҚжҮүзҡ„PIDжҮүи©Іжңғжңүиј•еҫ®зҡ„йҒҺиЎқпјҢеҸӘжҳҜжңүдәӣзі»зөұдёҚе…ҒиЁұйҒҺиЎқгҖӮеӣ жӯӨйңҖиҰҒе°ҮеӣһжҺҲзі»зөұиӘҝж•ҙзӮәйҒҺйҳ»е°јзі»зөұпјҢиҖҢ
еӨӘеӨ§жңғйҖ жҲҗйҹҝжҮүеӨӘеҝ«еҸҠйҒҺиЎқгҖӮдёҖиҲ¬иҖҢиЁҖеҝ«йҖҹеҸҚжҮүзҡ„PIDжҮүи©Іжңғжңүиј•еҫ®зҡ„йҒҺиЎқпјҢеҸӘжҳҜжңүдәӣзі»зөұдёҚе…ҒиЁұйҒҺиЎқгҖӮеӣ жӯӨйңҖиҰҒе°ҮеӣһжҺҲзі»зөұиӘҝж•ҙзӮәйҒҺйҳ»е°јзі»зөұпјҢиҖҢ жҜ”йҖ жҲҗйңҮзӣӘ
жҜ”йҖ жҲҗйңҮзӣӘ зҡ„дёҖеҚҠйӮ„иҰҒе°ҸеҫҲеӨҡгҖӮ
зҡ„дёҖеҚҠйӮ„иҰҒе°ҸеҫҲеӨҡгҖӮ
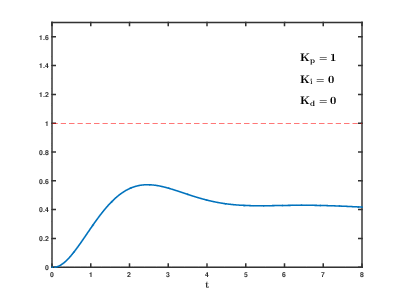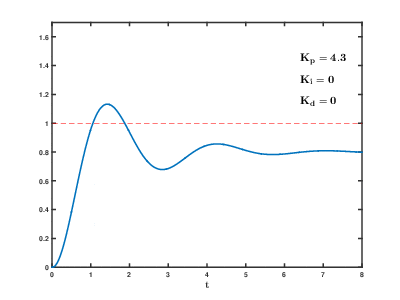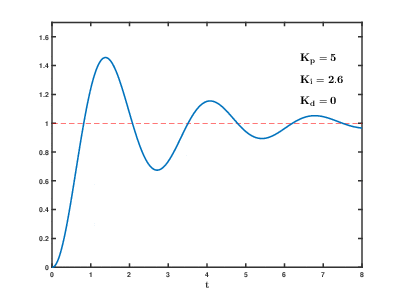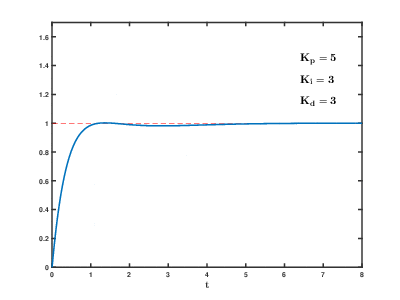 иӘҝж•ҙPIDеҸғж•ёе°Қе…¶жӯҘйҡҺйҹҝжҮүзҡ„еҪұйҹҝ
иӘҝж•ҙPIDеҸғж•ёе°Қе…¶жӯҘйҡҺйҹҝжҮүзҡ„еҪұйҹҝ
иӘҝж•ҙPIDеҸғж•ёе°Қзі»зөұзҡ„еҪұйҹҝеҰӮдёӢ
| иӘҝж•ҙж–№ејҸ |
(on) дёҠеҚҮж—¶й—ҙ |
и¶…и°ғйҮҸ |
е®үе®ҡж—¶й—ҙ |
зЁіжҖҒиҜҜе·® |
зЁіе®ҡжҖ§[10]
|
| вҶ‘ Kp |
жёӣе°‘ вҶ“ |
еўһеҠ вҶ‘ |
е°Ҹе№…еўһеҠ вҶ— |
жёӣе°‘ вҶ“ |
и®Ҡе·® вҶ“
|
| вҶ‘ Ki |
е°Ҹе№…жёӣе°‘ вҶҳ |
еўһеҠ вҶ‘ |
еўһеҠ вҶ‘ |
еӨ§е№…жёӣе°‘вҶ“вҶ“ |
и®Ҡе·®вҶ“
|
| вҶ‘ Kd |
е°Ҹе№…жёӣе°‘ вҶҳ |
жёӣе°‘вҶ“ |
жёӣе°‘вҶ“ |
и®ҠеӢ•дёҚеӨ§вҶ’ |
и®ҠеҘҪ вҶ‘
|
йҪҠж јеӢ’пјҚ尼科зҲҫж–Ҝж–№жі•
йҪҠж јеӢ’пјҚ尼科зҲҫж–Ҝж–№жі•жҳҜеҸҰдёҖзЁ®е•ҹзҷјејҸзҡ„иӘҝи©Ұж–№ејҸпјҢз”ұJohn G. Zieglerе’ҢNathaniel B. NicholsеңЁ1940е№ҙд»Је°Һе…ҘпјҢдёҖй–Ӣе§Ӣд№ҹжҳҜе°Ү еҸҠ
еҸҠ иЁӯе®ҡзӮәйӣ¶пјҢеўһеҠ жҜ”дҫӢеўһзӣҠзӣҙеҲ°зі»зөұй–Ӣе§ӢзӯүжҢҜе№…жҢҜзӣӘзӮәжӯўпјҢ當жҷӮзҡ„еўһзӣҠзЁұзӮә
иЁӯе®ҡзӮәйӣ¶пјҢеўһеҠ жҜ”дҫӢеўһзӣҠзӣҙеҲ°зі»зөұй–Ӣе§ӢзӯүжҢҜе№…жҢҜзӣӘзӮәжӯўпјҢ當жҷӮзҡ„еўһзӣҠзЁұзӮә пјҢиҖҢжҢҜзӣӘйҖұжңҹзӮә
пјҢиҖҢжҢҜзӣӘйҖұжңҹзӮә пјҢеҚіеҸҜз”Ёд»ҘдёӢзҡ„ж–№ејҸиЁҲз®—еўһзӣҠпјҡ
пјҢеҚіеҸҜз”Ёд»ҘдёӢзҡ„ж–№ејҸиЁҲз®—еўһзӣҠпјҡ
йҪҠж јеӢ’пјҚ尼科зҲҫж–Ҝж–№жі•
| жҺ§еҲ¶еҷЁзЁ®йЎһ
|

|

|

|
| P
|

|
-
|
-
|
| PI
|

|

|
-
|
| PID
|

|

|

|
PIDиӘҝи©Ұи»ҹй«”
еӨ§йғЁд»ҪзҸҫд»Јзҡ„е·ҘжҘӯиЁӯеӮҷдёҚеҶҚз”ЁдёҠиҝ°дәәе·ҘиЁҲз®—зҡ„ж–№ејҸиӘҝи©ҰпјҢиҖҢжҳҜз”ЁPIDиӘҝи©ҰеҸҠжңҖдҪіеҢ–и»ҹй«”дҫҶйҒ”еҲ°дёҖиҮҙзҡ„ж•ҲжһңгҖӮи»ҹй«”жңғ收йӣҶиіҮж–ҷпјҢе»әз«ӢжЁЎеһӢпјҢдёҰжҸҗдҫӣжңҖдҪізҡ„иӘҝи©ҰзөҗжһңпјҢжңүдәӣи»ҹй«”з”ҡиҮіеҸҜд»Ҙз”ЁеҸғиҖғе‘Ҫд»Өзҡ„и®ҠеҢ–дҫҶйҖІиЎҢиӘҝи©ҰгҖӮ
ж•ёеӯёзҡ„PIDиӘҝи©Ұжңғе°Үи„ҲиЎқеҠ е…Ҙзі»зөұпјҢеҶҚз”ЁеҸ—жҺ§зі»зөұзҡ„й »зҺҮйҹҝжҮүдҫҶиЁӯиЁҲPIDзҡ„еҸғж•ёгҖӮиӢҘжҳҜйҹҝжҮүжҷӮй–“иҰҒж•ёеҲҶйҗҳзҡ„зі»зөұпјҢе»әиӯ°з”Ёж•ёеӯёPIDиӘҝи©ҰпјҢеӣ зӮәз”Ёи©ҰиӘӨжі•еҸҜиғҪиҰҒиҠұдёҠе№ҫеӨ©жүҚиғҪжүҫеҲ°еҸҜи®“зі»зөұз©©е®ҡзҡ„еҸғж•ёгҖӮжңҖдҪіи§ЈдёҚеӨӘе®№жҳ“жүҫеҲ°пјҢжңүдәӣж•ёдҪҚзҡ„иҝҙи·ҜжҺ§еҲ¶еҷЁжңүиҮӘжҲ‘иӘҝи©Ұзҡ„зЁӢеәҸпјҢеҲ©з”Ёеҫ®е°Ҹзҡ„еҸғиҖғе‘Ҫд»ӨдҫҶиЁҲз®—жңҖдҪізҡ„иӘҝи©ҰеҖјгҖӮ
д№ҹжңүе…¶д»–иӘҝи©Ұзҡ„е…¬ејҸпјҢжҳҜдҫқдёҚеҗҢзҡ„жҖ§иғҪжә–еүҮжүҖз”ўз”ҹгҖӮиЁұеӨҡжңүе°ҲеҲ©зҡ„е…¬ејҸе·ІеөҢе…ҘеңЁPIDиӘҝи©Ұи»ҹй«”еҸҠзЎ¬й«”жЁЎзө„дёӯ[12]гҖӮ
дёҖдәӣе…ҲйҖІзҡ„PIDиӘҝи©Ұи»ҹй«”д№ҹеҸҜд»ҘеңЁеӢ•ж…Ӣзҡ„жғ…жіҒдёӢз”Ёжј”з®—жі•иӘҝж•ҙPIDиҝҙи·ҜпјҢйҖҷйЎһи»ҹй«”жңғе…Ҳе°ҮзЁӢеәҸе»әжЁЎпјҢзөҰеҫ®ж“ҫйҮҸпјҢеҶҚж №ж“ҡйҹҝжҮүиЁҲз®—еҸғж•ёгҖӮ
PIDжҺ§еҲ¶зҡ„йҷҗеҲ¶
PIDжҺ§еҲ¶еҸҜд»ҘжҮүз”ЁеңЁиЁұеӨҡжҺ§еҲ¶е•ҸйЎҢпјҢеӨҡеҚҠеңЁеӨ§з•ҘиӘҝж•ҙеҸғж•ёеҫҢе°ұжңүдёҚйҢҜзҡ„ж•ҲжһңпјҢдёҚйҒҺжңүдәӣжҮүз”ЁдёӢеҸҜиғҪеҸҚиҖҢжңғжңүе·®зҡ„ж•ҲжһңпјҢиҖҢдё”дёҖиҲ¬з„Ўжі•жҸҗдҫӣжңҖдҪіжҺ§еҲ¶гҖӮPIDжҺ§еҲ¶зҡ„дё»иҰҒе•ҸйЎҢжҳҜеңЁж–је…¶зӮәеӣһжҺҲжҺ§еҲ¶пјҢдҝӮж•ёзӮәе®ҡеҖјпјҢдёҚзҹҘйҒ“еҸ—жҺ§зі»зөұзҡ„иіҮиЁҠпјҢеӣ жӯӨе…¶ж•ҙдҪ“жҖ§иғҪеёёеёёжҳҜеҰҘеҚ”дёӢзҡ„зөҗжһңгҖӮеңЁжІ’жңүеҸ—жҺ§зі»зөұжЁЎеһӢзҡ„жўқ件дёӢпјҢPIDжҺ§еҲ¶жңҖдҪізҡ„жҺ§еҲ¶еҷЁ[2]пјҢдҪҶиӢҘй…ҚеҗҲзі»зөұжЁЎеһӢпјҢеҸҜд»ҘжңүйҖІдёҖжӯҘзҡ„жҸҗжҳҮгҖӮ
當PIDжҺ§еҲ¶еҷЁе–®зҚЁдҪҝз”ЁжҷӮпјҢиӢҘеӣ жҮүз”ЁйңҖжұӮпјҢйңҖиӘҝж•ҙPIDиҝҙи·ҜеўһзӣҠдҪҝжҺ§еҲ¶зі»зөұдёҚжңғйҒҺиЎқпјҢе…¶ж•ҲжһңжңүеҸҜиғҪеҫҲе·®гҖӮPIDжҺ§еҲ¶еҷЁзҡ„зјәй»һйӮ„еҢ…жӢ¬з„Ўжі•иҷ•зҗҶеҸ—жҺ§зі»зөұзҡ„йқһз·ҡжҖ§гҖҒйңҖеңЁеҸҚжҮүжҷӮй–“еҸҠи°ғж•ҙзҺҮд№Ӣй–“еҰҘеҚ”гҖҒз„Ўжі•йҮқе°ҚеҸғж•ёзҡ„и®ҠеӢ•иҖҢеҸҚжҮүпјҲдҫӢеҰӮзі»зөұеңЁжҡ–ж©ҹеҫҢзү№жҖ§жңғж”№и®ҠпјүгҖҒд»ҘеҸҠеӨ§ж“ҫеӢ•дёӢзҡ„жіўеҪўиҗҪеҫҢгҖӮ
PIDжҺ§еҲ¶еҷЁжңҖйЎҜи‘—зҡ„жҸҗжҳҮжҳҜй…ҚеҗҲеүҚйҘӢжҺ§еҲ¶пјҢеҠ е…Ҙжңүй—ңзі»зөұзҡ„иіҮиЁҠпјҢеҸӘз”ЁPIDжҺ§еҲ¶еҷЁдҫҶжҺ§еҲ¶иӘӨе·®гҖӮеҸҰеӨ–пјҢPIDжҺ§еҲ¶еҷЁд№ҹжңүдёҖдәӣе°Ҹе№…зҡ„ж”№е–„ж–№ејҸпјҢдҫӢеҰӮиӘҝж•ҙеҸғж•ёпјҲеўһзӣҠиҰҸеҠғжҲ–жҳҜдҫқжҖ§иғҪйҖІиЎҢйҒ©жҮүжҖ§зҡ„иӘҝж•ҙпјүгҖҒжҸҗжҳҮжҖ§иғҪпјҲжҸҗй«ҳеҸ–жЁЈзҺҮгҖҒзІҫеәҰеҸҠжә–еәҰпјҢиӢҘжңүйңҖиҰҒеҠ е…ҘдҪҺжіўжҝҫжіўеҷЁпјүпјҢжҲ–жҳҜз”ЁеӨҡеҖӢдёІжҺҘзҡ„PIDжҺ§еҲ¶еҷЁгҖӮ
з·ҡжҖ§
PIDжҺ§еҲ¶еҷЁеёёиҰӢзҡ„е•ҸйЎҢжҳҜеңЁж–је…¶з·ҡжҖ§дё”е°ҚзЁұзҡ„зү№жҖ§пјҢиӢҘжҮүз”ЁеңЁдёҖдәӣйқһз·ҡжҖ§зҡ„зі»зөұпјҢе…¶ж•ҲжһңеҸҜиғҪжңғжңүи®ҠеҢ–гҖӮд»Ҙжҡ–йҖҡз©әиӘҝдёӯеёёиҰӢзҡ„жә«еәҰжҺ§еҲ¶пјҢеҸҜиғҪжҳҜжҺЎз”Ёдё»еӢ•еҠ зҶұпјҲз”ЁеҠ зҶұеҷЁеҠ зҶұпјүпјҢдҪҶеҶ·еҚ»жҳҜдҪҝз”Ёиў«еӢ•еҶ·еҚ»пјҲдёҚеҠ зҶұпјҢиҮӘ然еҶ·еҚ»пјүпјҢе…¶еҶ·еҚ»йҖҹеәҰжҜ”еҠ зҶұйҖҹеәҰж…ўеҫҲеӨҡпјҢијёеҮәиӢҘжңүйҒҺиЎқпјҢдёӢйҷҚйҖҹеәҰеҫҲж…ўпјҢеӣ жӯӨPIDжҺ§еҲ¶йңҖиӘҝж•ҙзӮәдёҚжңғйҒҺиЎқзҡ„йҒҺйҳ»е°јпјҢд»Ҙжёӣе°‘жҲ–йҒҝе…ҚйҒҺиЎқпјҢдҪҶйҖҷд№ҹ延長дәҶж•ҙе®ҡжҷӮй–“пјҢдҪҝжҖ§иғҪи®Ҡе·®гҖӮ
йӣңиЁҠе°Қеҫ®еҲҶеҷЁзҡ„еҪұйҹҝ
еҫ®еҲҶеҷЁзҡ„е•ҸйЎҢеңЁж–је°ҚйҮҸжё¬жҲ–зЁӢеәҸз”ўз”ҹзҡ„й«ҳй »йӣңиЁҠжңғжңүж”ҫеӨ§ж•ҲжһңпјҢеӣ жӯӨжңғе°ҚијёеҮәйҖ жҲҗеӨ§е№…зҡ„и®ҠеӢ•гҖӮеӣ жӯӨзңҹеҜҰзҡ„жҺ§еҲ¶еҷЁдёҚжңғжңүзҗҶжғізҡ„еҫ®еҲҶеҷЁпјҢеҸӘжңүдёҖеҖӢжңүйҷҗй »еҜ¬зҡ„еҫ®еҲҶеҷЁжҲ–й«ҳйҖҡжҝҫжіўеҷЁгҖӮдёҖиҲ¬зӮәдәҶ移йҷӨй«ҳй »зҡ„йӣңиЁҠпјҢжңғеңЁйҮҸжё¬жҷӮеҠ е…ҘдҪҺйҖҡжҝҫжіўеҷЁпјҢиӢҘдҪҺйҖҡжҝҫжіўеҷЁе’Ңеҫ®еҲҶеҷЁе°Қж¶ҲпјҢжҝҫжіўж•Ҳжһңд№ҹе°ұеҸ—йҷҗдәҶпјҢеӣ жӯӨдҪҺйӣңиЁҠзҡ„йҮҸжё¬иЁӯеӮҷзӣёз•¶йҮҚиҰҒгҖӮеҜҰеӢҷдёҠеҸҜд»ҘдҪҝз”ЁдёӯеҖјж»ӨжіўеҷЁпјҢиӘҝжҳҮжҝҫжіўж•ҲзҺҮеҸҠеҜҰйҡӣдёҠзҡ„жҖ§иғҪ[13]гҖӮжңүжҷӮеҸҜд»Ҙе°Үеҫ®еҲҶеҷЁй—ңй–үпјҢе°ҚжҺ§еҲ¶жҖ§иғҪзҡ„еҪұйҹҝдёҚеӨ§пјҢжӯӨжҷӮзЁұзӮәPIжҺ§еҲ¶еҷЁгҖӮ
PIDжј”з®—жі•зҡ„дҝ®ж”№
еҹәжң¬зҡ„PIDжј”з®—жі•еңЁдёҖдәӣжҺ§еҲ¶жҮүз”Ёзҡ„жўқ件дёӢжңүдәӣдёҚи¶іпјҢйңҖйҖІиЎҢе°Ҹе№…зҡ„дҝ®ж”№гҖӮ
з©ҚеҲҶйЈҪе’Ң
з©ҚеҲҶйЈҪе’ҢжҳҜзҗҶжғіPIDжј”з®—жі•еҜҰзҸҫжҷӮеёёиҰӢзҡ„е•ҸйЎҢгҖӮиӢҘиЁӯе®ҡеҖјжңүеӨ§зҡ„и®ҠеӢ•пјҢе…¶з©ҚеҲҶйҮҸжңғжңүеӨ§е№…зҡ„и®ҠеҢ–пјҢеӨ§еҲ°ијёеҮәеҖјиў«дёҠдёӢйҷҗйҷҗеҲ¶иҖҢйЈҪе’ҢпјҢеӣ жӯӨзі»зөұжңғжңүйҒҺиЎқпјҢиҖҢдё”еҚідҪҝиӘӨе·®йҮҸз¬Ұиҷҹж”№и®ҠпјҢз©ҚеҲҶйҮҸи®Ҡе°ҸпјҢдҪҶијёеҮәеҖјд»Қиў«дёҠдёӢйҷҗйҷҗеҲ¶пјҢз¶ӯжҢҒеңЁдёҠйҷҗпјҲжҲ–дёӢйҷҗпјүпјҢеӣ жӯӨијёеҮәзңӢдјјжІ’жңүи®ҠеҢ–пјҢзі»зөұд»ҚжңғжҢҒзәҢзҡ„йҒҺиЎқпјҢдёҖзӣҙиҰҒеҲ°ијёеҮәеҖјиҗҪеңЁдёҠдёӢйҷҗзҡ„зҜ„еңҚе…§пјҢзі»зөұзҡ„еӣһжҺҲйҮҸжүҚжңғй–Ӣе§ӢдёӢйҷҚгҖӮжӯӨе•ҸйЎҢеҸҜд»Ҙз”Ёд»ҘдёӢж–№ејҸиҷ•зҗҶпјҡ
- еңЁзЁӢеәҸи®Ҡж•ёйӣўй–ӢеҸҜжҺ§еҲ¶зҜ„еңҚжҷӮпјҢжҡ«еҒңз©ҚеҲҶгҖӮ
- и®“з©ҚеҲҶеҖјйҷҗеҲ¶еңЁдёҖеҖӢијғе°Ҹзҡ„дёҠдёӢзҜ„еңҚе…§гҖӮ
- йҮҚж–°иЁҲз®—з©ҚеҲҶй …пјҢдҪҝжҺ§еҲ¶еҷЁијёеҮәз¶ӯжҢҒдёҠдёӢйҷҗд№Ӣй–“зҡ„зҜ„еңҚе…§[14]гҖӮ
PIжҺ§еҲ¶еҷЁ
 PIжҺ§еҲ¶еҷЁзҡ„ж–№еЎҠең–
PIжҺ§еҲ¶еҷЁзҡ„ж–№еЎҠең–
PIжҺ§еҲ¶еҷЁпјҲжҜ”дҫӢ-з©ҚеҲҶжҺ§еҲ¶еҷЁпјүжҳҜдёҚз”Ёеҫ®еҲҶе–®е…ғзҡ„PIDжҺ§еҲ¶еҷЁгҖӮ
жҺ§еҲ¶еҷЁзҡ„ијёеҮәзӮә

е…¶дёӯ зӮәиЁӯе®ҡеҖјSPе’ҢйҮҸжё¬еҖјPVзҡ„иӘӨе·®пјҡ
зӮәиЁӯе®ҡеҖјSPе’ҢйҮҸжё¬еҖјPVзҡ„иӘӨе·®пјҡ
 .
.
PIжҺ§еҲ¶еҷЁеҸҜд»Ҙз”ЁSimulinkжҲ–Xcosд№ӢйЎһзҡ„и»ҹй«”йҖІиЎҢе»әжЁЎпјҢж–№ејҸжҳҜдҪҝз”ЁгҖҢflow chartгҖҚең–жЎҶпјҢе…¶дёӯз”Ёд»ҘдёӢзҡ„жӢүж°ҸйҒӢз®—еӯҗпјҡ

е…¶дёӯ
 = жҜ”дҫӢеўһзӣҠ
= жҜ”дҫӢеўһзӣҠ = з©ҚеҲҶеўһзӣҠ
= з©ҚеҲҶеўһзӣҠ
 еҖјзҡ„йҒёж“ҮйңҖеңЁжёӣе°‘йҒҺиЎқд»ҘеҸҠеўһеҠ е®үе®ҡжҷӮй–“д№Ӣй–“еҸ–жҚЁгҖӮ
еҖјзҡ„йҒёж“ҮйңҖеңЁжёӣе°‘йҒҺиЎқд»ҘеҸҠеўһеҠ е®үе®ҡжҷӮй–“д№Ӣй–“еҸ–жҚЁгҖӮ
еҫ®еҲҶе–®е…ғе°Қијёе…Ҙдёӯзҡ„й«ҳй »дҝЎиҷҹж јеӨ–ж•Ҹж„ҹпјҢPIжҺ§еҲ¶еҷЁеӣ зӮәжІ’жңүеҫ®еҲҶе–®е…ғпјҢеңЁиЁҠиҷҹйӣңиЁҠеӨ§жҷӮпјҢеңЁз©©ж…ӢжҷӮжңғжӣҙеҠ з©©е®ҡгҖӮдҪҶе°ҚзӢҖж…Ӣеҝ«йҖҹи®ҠеҢ–зҡ„еҸҚжҮүијғж…ўпјҢеӣ жӯӨзӣёијғж–јиӘҝйҒ©еҲ°жңҖдҪіеҖјзҡ„PIDжҺ§еҲ¶еҷЁпјҢPIжҺ§еҲ¶еҷЁжңғијғж…ўеҲ°йҒ”иЁӯе®ҡеҖјпјҢеҸ—е№Іж“ҫеҫҢд№ҹжҜ”ијғж…ўжҒўеҫ©еҲ°жӯЈеёёеҖјгҖӮ
PDFжҺ§еҲ¶пјҲpseudo-derivative feedback controlпјүеҸҜд»ҘиҰ–зӮәжҳҜPIжҺ§еҲ¶еҷЁзҡ„и®Ҡй«”пјҢжҜ”дҫӢжҺ§еҲ¶еҷЁзҡ„ијёе…Ҙз”ұиӘӨе·®еҖјж”№зӮәеӣһжҺҲеҖј[15]гҖӮ
дёҚеӢ•дҪңеҚҖ
иЁұеӨҡPIDиҝҙи·ҜжҳҜжҺ§еҲ¶ж©ҹжў°е…ғ件пјҲдҫӢеҰӮй–ҘпјүгҖӮж©ҹжў°дҝқйӨҠжҳҜдёҖзӯҶеҸҜи§Җзҡ„иІ»з”ЁпјҢзЈЁжҗҚжңғдҪҝеҫ—ж©ҹжў°еңЁжңүијёе…ҘдҝЎиҷҹжҷӮеҮәзҸҫйқңж‘©ж“ҰжҲ–жҳҜдёҚеӢ•дҪңеҚҖпјҢйғҪжңғе°ҺиҮҙжҺ§еҲ¶жҖ§иғҪзҡ„дёӢйҷҚгҖӮж©ҹжў°жҗҚиҖ—зҡ„йҖҹеәҰдё»иҰҒе’ҢиЁӯеӮҷеӨҡеёёж”№и®Ҡе…¶зӢҖж…Ӣжңүй—ңгҖӮиӢҘзЈЁжҗҚжҳҜдё»иҰҒиҖғйҮҸзҡ„и©ұпјҢPIDиҝҙи·ҜеҸҜд»ҘжңүијёеҮәзҡ„йҒІж»ҜзҸҫиұЎд»Ҙжёӣе°‘ијёеҮәзӢҖж…Ӣзҡ„ж”№и®ҠгҖӮиӢҘи®ҠеҢ–е°ҸпјҢд»ҚеңЁдёҚеӢ•дҪңеҚҖе…§пјҢи®“жҺ§еҲ¶еҷЁзҡ„ијёеҮәз¶ӯжҢҒдёҠдёҖж¬Ўзҡ„еҖјгҖӮи®ҠеҢ–иҰҒеӨ§еҲ°и¶…йҒҺдёҚеӢ•дҪңеҚҖпјҢеҜҰйҡӣзҡ„зӢҖж…ӢжүҚжңғйҡЁд№Ӣи®ҠеҢ–гҖӮ
иЁӯе®ҡеҖјзҡ„жӯҘйҡҺи®ҠеҢ–
иӢҘзі»зөұзҡ„иЁӯе®ҡеҖјжңүжӯҘйҡҺи®ҠеҢ–пјҢжҜ”дҫӢе–®е…ғе’Ңеҫ®еҲҶе–®е…ғд№ҹжңғжңүе°ҚжҮүзҡ„и®ҠеҢ–пјҢзү№еҲҘжҳҜеҫ®еҲҶе–®е…ғе°Қж–јжӯҘйҡҺи®ҠеҢ–зҡ„ијёеҮәзү№еҲҘзҡ„еӨ§пјҢеӣ жӯӨжңүдәӣPIDжј”з®—жі•жңғй…ҚеҗҲд»ҘдёӢзҡ„дҝ®ж”№дҫҶиҷ•зҗҶиЁӯе®ҡеҖјзҡ„и®ҠеҢ–гҖӮ
- иЁӯе®ҡеҖјж–ңеқЎи®ҠеҢ–
- жӯӨдҝ®ж”№ж–№ејҸдёӢпјҢиЁӯе®ҡеҖјжңғз”Ёз·ҡжҖ§жҲ–жҳҜдёҖйҡҺжҝҫжіўзҡ„ж–№ејҸпјҢз”ұеҺҹе§ӢеҖји®ҠеҲ°ж–°зҡ„еҖјпјҢйҒҝе…Қеӣ зӮәжӯҘйҡҺи®ҠеҢ–з”ўз”ҹзҡ„дёҚйҖЈзәҢгҖӮ
- еҸӘе°ҚзЁӢеәҸи®Ҡж•ёпјҲеӣһжҺҲйҮҸпјүеҫ®еҲҶ
- жӯӨдҝ®ж”№дёӢпјҢPIDжҺ§еҲ¶еҷЁеҸӘйҮқе°ҚйҮҸжё¬зҡ„зЁӢеәҸи®Ҡж•ёпјҲPVпјүеҫ®еҲҶпјҢдёҚе°ҚиӘӨе·®еҫ®еҲҶгҖӮзЁӢеәҸи®Ҡж•ёжҳҜеҜҰйҡӣзҡ„зү©зҗҶйҮҸпјҢијғдёҚжҳ“жңүзһ¬й–“зҡ„и®ҠеҢ–пјҢиҖҢиӘӨе·®еҸҜиғҪеӣ зӮәиЁӯе®ҡеҖјзҡ„жӯҘйҡҺи®ҠеҢ–иҖҢжңүзһ¬й–“и®ҠеҢ–гҖӮйҖҷд№ҹжҳҜдёҖзЁ®з°Ўе–®зҡ„иЁӯе®ҡеҖјеҠ ж¬Ҡжі•гҖӮ
- иЁӯе®ҡеҖјеҠ ж¬Ҡ
- иЁӯе®ҡеҖјеҠ ж¬ҠеҲҶеҲҘиӘҝж•ҙеңЁжҜ”дҫӢе–®е…ғеҸҠеҫ®еҲҶе–®е…ғдёӯзҡ„иӘӨе·®йҮҸпјҢиӘӨе·®йҮҸзҡ„иЁӯе®ҡеҖјд№ҳд»ҘдёҖеҖӢ0еҲ°1д№Ӣй–“зҡ„еҠ ж¬ҠпјҢз©ҚеҲҶе–®е…ғзҡ„иӘӨе·®йҮҸйңҖдҪҝз”ЁзңҹеҜҰзҡ„иЁӯе®ҡеҖјпјҢд»ҘйҒҝе…Қз©©ж…ӢиӘӨе·®гҖӮйҖҷе…©еҖӢеҸғж•ёдёҚеҪұйҹҝе°ҚиІ ијүи®ҠеҢ–еҸҠйҮҸжё¬йӣңиЁҠзҡ„йҹҝжҮүпјҢеҸҜд»ҘжҸҗжҳҮе°ҚиЁӯе®ҡй»һи®ҠеҢ–зҡ„йҹҝжҮүгҖӮ
еүҚйҘӢжҺ§еҲ¶
PIDжҺ§еҲ¶еҷЁиӢҘеҶҚй…ҚеҗҲеүҚйҘӢжҺ§еҲ¶пјҲй–Ӣиҝҙи·ҜжҺ§еҲ¶пјүпјҢеҸҜд»ҘеҶҚжҸҗжҳҮе…¶жҺ§еҲ¶жҖ§иғҪгҖӮеңЁеүҚйҘӢжҺ§еҲ¶дёӯиҖғж…®зі»зөұзҡ„е·ІзҹҘиіҮиЁҠпјҲдҫӢеҰӮзҗҶжғіеҠ йҖҹеәҰжҲ–жҳҜж…ЈйҮҸпјүпјҢеҶҚе°ҮијёеҮәеҠ еҲ°PIDжҺ§еҲ¶еҷЁзҡ„жҺ§еҲ¶ијёеҮәпјҢд»ҘжҸҗжҳҮж•ҙй«”зҡ„зі»зөұжҖ§иғҪгҖӮеүҚйҘӢйҮҸеҸҜиғҪжҳҜжҺ§еҲ¶ијёеҮәдё»иҰҒзҡ„йғЁд»ҪпјҢиҖҢPIDжҺ§еҲ¶еҷЁеҸӘз”ЁдҫҶиЈңе„ҹзӣ®жЁҷеҖје’Ңй–Ӣиҝҙи·ҜжҺ§еҲ¶еҷЁијёеҮәд№Ӣй–“зҡ„иӘӨе·®гҖӮеӣ зӮәеүҚйҘӢијёеҮәдёҚжңғеҸ—еҲ°еӣһжҺҲзҡ„еҪұйҹҝпјҢеӣ жӯӨд№ҹдёҚжңғйҖ жҲҗзі»зөұзҡ„жҢҜзӣӘпјҢеҸҜд»ҘеңЁдёҚеҪұйҹҝз©©е®ҡжҖ§зҡ„жўқ件дёӢжҸҗжҳҮзі»зөұзҡ„йҹҝжҮүгҖӮеүҚйҘӢеҸҜд»Ҙдҫқзӣ®жЁҷеҖјеҸҠе…¶д»–йҮҸжё¬еҲ°зҡ„е№Іж“ҫйҮҸдҫҶз”ўз”ҹпјҢзӣ®жЁҷеҖјеҠ ж¬ҠжҳҜдёҖзЁ®з°Ўе–®зҡ„еүҚйҘӢжҺ§еҲ¶ж–№ејҸгҖӮ
дҫӢеҰӮпјҢеңЁеӨ§йғЁд»Ҫзҡ„йҒӢеӢ•жҺ§еҲ¶зі»зөұдёӯпјҢзӮәдәҶиҰҒдҪҝж©ҹжў°иІ ијүеҠ йҖҹпјҢиҮҙеӢ•еҷЁиҰҒз”ўз”ҹжӣҙеӨ§зҡ„еҠӣгҖӮиӢҘз”ЁйҖҹеәҰз’°зҡ„PIDжҺ§еҲ¶еҷЁдҫҶжҺ§еҲ¶иІ ијүйҖҹеәҰпјҢжҜ”ијғзҗҶжғізҡ„ж–№ејҸжҳҜе…Ҳеҫ—еҲ°зҗҶжғізҡ„зһ¬й–“еҠ йҖҹеәҰеҖјпјҢйҒ©йҮҸиӘҝж•ҙеҠ ж¬ҠеҫҢеҶҚеҠ еҲ°PIDзҡ„ијёеҮәдёӯгҖӮеӣ жӯӨжҺ§еҲ¶еҷЁијёеҮәдёӯжңүдёҖйғЁд»ҪжҳҜдёҚйҡЁж©ҹжў°йҖҹеәҰиҖҢж”№и®Ҡзҡ„ијёеҮәпјҢеҶҚз”ЁPIDж №ж“ҡеҜҰйҡӣијёеҮәе’Ңзӣ®жЁҷзҡ„е·®з•°еҺ»еўһеҠ жҲ–жҳҜжёӣе°‘ијёеҮәгҖӮйҖҷйЎһжңүеүҚйҘӢжҺ§еҲ¶зҡ„PIDжҺ§еҲ¶еҷЁеҸҜд»ҘеҠ еҝ«жҺ§еҲ¶зі»зөұзҡ„еҸҚжҮүйҖҹеәҰгҖӮ
з„ЎиЎқж“ҠйҒӢиҪү
жңүжҷӮPIDжҺ§еҲ¶еҷЁжңғиҰҸеҠғзӮәз„ЎиЎқж“ҠпјҲbumplessпјүзҡ„зү№жҖ§пјҢеңЁеҸғж•ёи®ҠеҢ–жҷӮйҮҚж–°иЁҲз®—йҒ©з•¶зҡ„з©ҚеҲҶзҙҜиЁҲеҖјпјҢдҪҝијёеҮәдёҚжңғеӣ еҸғж•ёи®ҠеҢ–жңүдёҚйҖЈзәҢзҡ„ж”№и®Ҡ[16]гҖӮ
дёІзҙҡPIDжҺ§еҲ¶еҷЁ
дәҢеҖӢPIDжҺ§еҲ¶еҷЁеҸҜд»Ҙзө„еҗҲеңЁдёҖиө·пјҢеҫ—еҲ°ијғдҪізҡ„ж•ҲжһңпјҢйҖҷзЁұзӮәдёІзҙҡPIDжҺ§еҲ¶гҖӮд»Ҙе…©еҖӢPIDжҺ§еҲ¶еҷЁзө„жҲҗзҡ„дёІзҙҡPIDжҺ§еҲ¶зӮәдҫӢпјҢе…¶дёӯдёҖеҖӢPIDжҺ§еҲ¶еҷЁеңЁеӨ–иҝҙи·ҜпјҢжҺ§еҲ¶еғҸж¶Ійқўй«ҳеәҰжҲ–жҳҜйҖҹеәҰзӯүдё»иҰҒзҡ„зү©зҗҶйҮҸпјҢеҸҰдёҖеҖӢPIDжҺ§еҲ¶еҷЁжҳҜе…§иҝҙи·ҜпјҢд»ҘеӨ–иҝҙи·ҜPIDжҺ§еҲ¶еҷЁзҡ„ијёеҮәеҒҡзӮәе…¶зӣ®жЁҷеҖјпјҢдёҖиҲ¬жҳҜжҺ§еҲ¶ијғеҝ«йҖҹи®ҠеҢ–зҡ„еҸғж•ёпјҢдҫӢеҰӮжөҒйҮҸжҲ–еҠ йҖҹеәҰзӯүгҖӮиӢҘеҲ©з”ЁдёІзҙҡPIDжҺ§еҲ¶пјҢеҸҜд»ҘеўһеҠ жҺ§еҲ¶еҷЁзҡ„е·ҘдҪңй »зҺҮпјҢдёҰйҷҚдҪҺе…¶жҷӮй–“еёёж•ёгҖӮ
дҫӢеҰӮдёҖеҖӢжә«жҺ§зҡ„еҫӘз’°ж°ҙжөҙиЁӯеӮҷжңүдәҢеҖӢдёІзҙҡзҡ„PIDжҺ§еҲ¶еҷЁпјҢеҲҶеҲҘжңүеҗ„иҮӘзҡ„зҶұйӣ»еҒ¶жә«еәҰж„ҹжё¬еҷЁгҖӮеӨ–иҝҙи·Ҝзҡ„жҺ§еҲ¶еҷЁжҺ§еҲ¶ж°ҙжә«пјҢе…¶ж„ҹжё¬еҷЁи·қеҠ зҶұеҷЁеҫҲйҒ пјҢзӣҙжҺҘйҮҸжё¬ж•ҙй«”ж°ҙжә«пјҢе…¶иӘӨе·®йҮҸжҳҜзҗҶжғіж°ҙжә«еҸҠж•ҙй«”ж°ҙжә«зҡ„е·®еҖјгҖӮеӨ–иҝҙи·ҜPIDжҺ§еҲ¶еҷЁзҡ„иҫ“еҮәеҚізӮәе…§иҝҙи·ҜжҺ§еҲ¶еҷЁзҡ„зӣ®жЁҷеҖјпјҢе…§иҝҙи·ҜжҺ§еҲ¶еҷЁжҺ§еҲ¶еҠ зҶұеҷЁпјҢе…¶ж„ҹжё¬еҷЁжҳҜеңЁеҠ зҶұеҷЁдёҠпјҢе…¶иӘӨе·®йҮҸжҳҜеҠ зҶұеҷЁзҡ„зҗҶжғіжә«еәҰеҸҠйҮҸжё¬еҲ°жә«еәҰзҡ„е·®еҖјпјҢе…¶ијёеҮәжңғдҪҝеҠ зҶұеҷЁз¶ӯжҢҒеңЁиЁӯе®ҡеҖјйҷ„иҝ‘гҖӮ
е…§еӨ–иҝҙи·ҜжҺ§еҲ¶еҷЁзҡ„еҸғж•ёеҸҜиғҪжңғе·®еҫҲеӨҡпјҢеӨ–иҝҙи·Ҝзҡ„PIDжҺ§еҲ¶еҷЁжңүијғй•·зҡ„жҷӮй–“еёёж•ёпјҢе°ҚжҮүжүҖжңүзҡ„ж°ҙеҠ зҶұжҲ–жҳҜеҶ·еҚ»йңҖиҰҒзҡ„жҷӮй–“гҖӮе…§иҝҙи·Ҝзҡ„PIDжҺ§еҲ¶еҷЁеҸҚжҮүжңғжҜ”ијғеҝ«гҖӮжҜҸеҖӢжҺ§еҲ¶еҷЁеҸҜд»ҘиӘҝж•ҙеҲ°з¬ҰеҗҲе…¶зңҹжӯЈжҺ§еҲ¶зҡ„зі»зөұпјҢдҫӢеҰӮж°ҙж§ҪдёӯжүҖжңүзҡ„ж°ҙпјҢжҲ–жҳҜеҠ зҶұеҷЁжң¬иә«гҖӮ
е…¶д»–PIDзҡ„еҪўејҸеҸҠе…¶иЎЁзӨәжі•
зҗҶжғізҡ„PIDеҸҠжЁҷжә–еҪўPID
е·ҘжҘӯдёҠеёёзңӢеҲ°PIDжҺ§еҲ¶еҷЁпјҢиҖҢиЁұеӨҡе·ҘжҘӯзӣёй—ңиіҮж–ҷдёӯзңӢеҲ°зҡ„йғҪжҳҜгҖҢжЁҷжә–еҪўгҖҚзҡ„PIDпјҢе…¶дёӯжҜ”дҫӢеўһзӣҠ д№ҹдҪңз”ЁеңЁ
д№ҹдҪңз”ЁеңЁ еҸҠ
еҸҠ е…©й …пјҢе’ҢдёҠиҝ°гҖҢзҗҶи«–гҖҚж®өиҗҪзңӢеҲ°зҡ„еҪўејҸдёҚеҗҢгҖӮгҖҢжЁҷжә–еҪўгҖҚзҡ„PIDзӮәпјҡ
е…©й …пјҢе’ҢдёҠиҝ°гҖҢзҗҶи«–гҖҚж®өиҗҪзңӢеҲ°зҡ„еҪўејҸдёҚеҗҢгҖӮгҖҢжЁҷжә–еҪўгҖҚзҡ„PIDзӮәпјҡ

е…¶дёӯ
 зӮәз©ҚеҲҶжҷӮй–“
зӮәз©ҚеҲҶжҷӮй–“ зӮәеҫ®еҲҶжҷӮй–“
зӮәеҫ®еҲҶжҷӮй–“
еңЁжЁҷжә–еҪўдёӯпјҢжҜҸдёҖеҖӢеҸғж•ёжңүе…¶жҳҺзўәзҡ„зү©зҗҶж„Ҹзҫ©пјҢијёеҮәжҳҜж №ж“ҡзҸҫеңЁиӘӨе·®гҖҒйҒҺеҺ»иӘӨе·®еҸҠжңӘдҫҶиӘӨе·®иҖҢжұәе®ҡпјҢеҠ дёҠеҫ®еҲҶй …еҸҜд»Ҙй җжё¬иӢҘжҺ§еҲ¶зі»зөұдёҚж”№и®Ҡзҡ„и©ұпјҢ жҷӮй–“еҫҢзҡ„иӘӨе·®пјҢиҖҢз©ҚеҲҶй …жҳҜз”ЁйҒҺеҺ»жүҖжңүиӘӨе·®зҡ„е’ҢдҫҶиӘҝж•ҙијёеҮәпјҢеёҢжңӣеңЁ
жҷӮй–“еҫҢзҡ„иӘӨе·®пјҢиҖҢз©ҚеҲҶй …жҳҜз”ЁйҒҺеҺ»жүҖжңүиӘӨе·®зҡ„е’ҢдҫҶиӘҝж•ҙијёеҮәпјҢеёҢжңӣеңЁ жҷӮй–“еҫҢеҸҜд»Ҙе®Ңе…Ёж¶ҲйҷӨиӘӨе·®пјҢиҖҢијёеҮәзҡ„еҖјжңғеҶҚд№ҳд»Ҙе–®дёҖзҡ„еўһзӣҠ
жҷӮй–“еҫҢеҸҜд»Ҙе®Ңе…Ёж¶ҲйҷӨиӘӨе·®пјҢиҖҢијёеҮәзҡ„еҖјжңғеҶҚд№ҳд»Ҙе–®дёҖзҡ„еўһзӣҠ гҖӮ
гҖӮ
еңЁзҗҶжғізҡ„е№іиЎҢејҸPIDдёӯпјҢе…¶ж–№зЁӢеҰӮдёӢпјҡ

е…¶дёӯзҡ„еўһзӣҠе’ҢжЁҷжә–еҪўPIDдҝӮж•ёзҡ„й—ңдҝӮжҳҜпјҡ еҸҠ
еҸҠ гҖӮе№іиЎҢејҸPIDдёӯзҡ„еҸғж•ёйғҪиҰ–зӮәе–®зҙ”зҡ„еўһзӣҠпјҢжңҖжіӣз”ЁпјҢйқҲжҙ»жҖ§д№ҹжңҖй«ҳпјҢдҪҶијғжІ’жңүзү©зҗҶж„Ҹзҫ©пјҢеӣ жӯӨеҸӘз”ЁеңЁPIDзҡ„зҗҶи«–иҷ•зҗҶдёӯпјҢжЁҷжә–еҪўPIDйӣ–еңЁж•ёеӯёдёҠжҜ”ијғиӨҮйӣңпјҢеңЁе·ҘжҘӯдёӯијғеёёдҪҝз”ЁгҖӮ
гҖӮе№іиЎҢејҸPIDдёӯзҡ„еҸғж•ёйғҪиҰ–зӮәе–®зҙ”зҡ„еўһзӣҠпјҢжңҖжіӣз”ЁпјҢйқҲжҙ»жҖ§д№ҹжңҖй«ҳпјҢдҪҶијғжІ’жңүзү©зҗҶж„Ҹзҫ©пјҢеӣ жӯӨеҸӘз”ЁеңЁPIDзҡ„зҗҶи«–иҷ•зҗҶдёӯпјҢжЁҷжә–еҪўPIDйӣ–еңЁж•ёеӯёдёҠжҜ”ијғиӨҮйӣңпјҢеңЁе·ҘжҘӯдёӯијғеёёдҪҝз”ЁгҖӮ
еҖ’ж•ёеўһзӣҠ
иЁұеӨҡжғ…еҪўдёӢпјҢPIDжҺ§еҲ¶еҷЁиҷ•зҗҶзҡ„и®Ҡж•ёжҳҜз„Ўеӣ ж¬Ўзҡ„йҮҸпјҢжҳҜжҹҗеҖӢжңҖеӨ§еҖјзҡ„жҜ”дҫӢпјҢд»Ӣж–ј0еҲ°100%д№Ӣй–“пјҢиҖҢиҪүжҸӣзӮәеҜҰйҡӣзү©зҗҶйҮҸпјҲеҰӮжіөжөҰйҖҹзҺҮжҲ–жҳҜж°ҙеҠ зҶұзҡ„еҠҹзҺҮпјүжҳҜеңЁPIDжҺ§еҲ¶еҷЁеӨ–пјҢиҖҢйҖҷдәӣжҺ§еҲ¶и®Ҡж•ёжҳҜжңүеӣ ж¬Ўзҡ„зү©зҗҶйҮҸпјҲдҫӢеҰӮжә«еәҰпјүгҖӮжӯӨжҷӮ еўһзӣҠеӨҡеҚҠдёҚжңғиЎЁзӨәзӮәгҖҢжҜҸи®ҠеҢ–дёҖеәҰзҡ„ијёеҮәгҖҚпјҢиҖҢжңғд»Ҙжә«еәҰзҡ„еҪўејҸ
еўһзӣҠеӨҡеҚҠдёҚжңғиЎЁзӨәзӮәгҖҢжҜҸи®ҠеҢ–дёҖеәҰзҡ„ијёеҮәгҖҚпјҢиҖҢжңғд»Ҙжә«еәҰзҡ„еҪўејҸ иЎЁзӨәпјҢд»ЈиЎЁгҖҢ100%ијёеҮәдёӢзҡ„жә«еәҰпјҲи®ҠеҢ–пјүгҖҚпјҢд»ЈиЎЁијёеҮәз”ұ0и®ҠеҲ°1пјҲ0%и®ҠзӮә100%пјүдёӢзҡ„жә«еәҰи®ҠеҢ–гҖӮ
иЎЁзӨәпјҢд»ЈиЎЁгҖҢ100%ијёеҮәдёӢзҡ„жә«еәҰпјҲи®ҠеҢ–пјүгҖҚпјҢд»ЈиЎЁијёеҮәз”ұ0и®ҠеҲ°1пјҲ0%и®ҠзӮә100%пјүдёӢзҡ„жә«еәҰи®ҠеҢ–гҖӮ
еҸӘйҮқе°ҚйҒҺзЁӢи®Ҡж•ёйҖІиЎҢеҫ®еҲҶжҺ§еҲ¶
еңЁеӨ§йғЁд»Ҫзҡ„е•ҶжҘӯжҺ§еҲ¶зі»зөұдёӯпјҢжҳҜз”ЁйҒҺзЁӢи®Ҡж•ёеҸ–д»ЈиӘӨе·®дҪңзӮәеҫ®еҲҶй …зҡ„ијёе…ҘпјҢе…¶еҺҹеӣ жҳҜ當зӣ®жЁҷеҖјжңүдёҚйҖЈзәҢи®ҠеҢ–жҷӮпјҢеҫ®еҲҶжҺ§еҲ¶жңғз”ўз”ҹеҫҲеӨ§зҡ„зӘҒжіўпјҢиӢҘзӣ®жЁҷеҖјдёҚи®ҠпјҢж”№и®ҠйҒҺзЁӢи®Ҡж•ёзҡ„ж•Ҳжһңе’Ңж”№и®ҠиӘӨе·®зӣёеҗҢпјҢеӣ жӯӨжңүдәӣPIDжҺ§еҲ¶еҷЁжңғз”ЁйҒҺзЁӢи®Ҡж•ёдҪңзӮәеҫ®еҲҶй …зҡ„ијёе…ҘпјҢдёҚжңғеҪұйҹҝжҺ§еҲ¶еҷЁжҺ§еҲ¶йҒҺзЁӢи®Ҡж•ёпјҢжҠ—йӣңиЁҠзҡ„иғҪеҠӣгҖӮ

еҸӘйҮқе°ҚйҒҺзЁӢи®Ҡж•ёйҖІиЎҢеҫ®еҲҶеҸҠжҜ”дҫӢжҺ§еҲ¶
еӨ§йғЁд»Ҫзҡ„е•ҶжҘӯжҺ§еҲ¶зі»зөұд№ҹжҸҗдҫӣйҒёж“ҮпјҢи®“йҒҺзЁӢи®Ҡж•ёдҪңзӮәеҫ®еҲҶжҺ§еҲ¶еҸҠжҜ”дҫӢжҺ§еҲ¶зҡ„ијёе…ҘпјҢеӣ жӯӨиӘӨе·®еҸӘдҪңзӮәз©ҚеҲҶжҺ§еҲ¶зҡ„ијёе…ҘпјҢйҖҷд№ҹдёҚжңғеҪұйҹҝжҺ§еҲ¶еҷЁжҺ§еҲ¶йҒҺзЁӢи®Ҡж•ёпјҢжҠ—йӣңиЁҠзҡ„иғҪеҠӣгҖӮ
дёҠиҝ°зҡ„дҝ®ж”№еҸҜд»ҘйҒҝе…Қзӣ®жЁҷеҖјжңүдёҚйҖЈзәҢи®ҠеҢ–жҷӮпјҢијёеҮәеҖјжңүе°ҚжҮүдёҚйҖЈзәҢзҡ„и®ҠеҢ–пјҢиӢҘзӣ®жЁҷеҖјжңүжӯҘйҡҺи®ҠеҢ–пјҢйҖҷй …иӘҝж•ҙе°ұзӣёз•¶йҮҚиҰҒгҖӮ

д№ҹжңүдәӣйӣҷиҮӘз”ұеәҰпјҲ2-DoFпјүPIDжҺ§еҲ¶жһ¶ж§ӢйҷӨдәҶдёҖиҲ¬зҡ„PIDжҺ§еҲ¶еӨ–пјҢеҶҚеҠ дёҠеҸӘйҮқе°ҚйҒҺзЁӢи®Ҡж•ёйҖІиЎҢзҡ„еҫ®еҲҶеҸҠжҜ”дҫӢжҺ§еҲ¶пјҢеҶҚеҲҶеҲҘз”ЁеўһзӣҠйҖІиЎҢиӘҝж•ҙпјҢзӣ®жЁҷжҳҜеҗҢжҷӮе°Қзӣ®жЁҷжӯҘйҡҺйҹҝжҮүд»ҘеҸҠйӣңиЁҠжҠ‘еҲ¶йғҪжңүиүҜеҘҪзҡ„жҖ§иғҪ[17]гҖӮ
PIDжҺ§еҲ¶еҷЁзҡ„жӢүж°ҸиҪүжҸӣ
жңүй—ңжңғе°ҮPIDжҺ§еҲ¶еҷЁйҖІиЎҢжӢүж°ҸиҪүжҸӣпјҡ

PIDжҺ§еҲ¶еҷЁзҡ„жӢүж°ҸиҪүжҸӣд№ҹд»ЈиЎЁи‘—жҺ§еҲ¶еҷЁзҡ„еӮійҒһеҮҪж•ёпјҢеӣ жӯӨеҸҜд»ҘзўәиӘҚж•ҙй«”зі»зөұзҡ„еӮійҒһеҮҪж•ёгҖӮ
PIDзҡ„жҘөйӣ¶й»һе°Қж¶Ҳ
PIDжҺ§еҲ¶еҷЁеҸҜд»ҘеҜ«жҲҗд»ҘдёӢзҡ„еҪўејҸ

иӢҘеҸ—жҺ§иЁӯеӮҷзҡ„еӮійҒһеҮҪж•ёеҰӮдёӢпјҡ

еҸҲд»Ө


еүҮ

еӣ жӯӨиӢҘеҸ—жҺ§иЁӯеӮҷжңүдёҚз©©е®ҡзҡ„жҘөй»һпјҢзңӢдјјеҸҜд»Ҙз”ЁжӯӨж–№ејҸж¶ҲйҷӨпјҢдёҚйҒҺеҜҰйҡӣдёҠжңүдәӣе·®з•°пјҢз”ұе№Іж“ҫеҲ°ијёеҮәзҡ„й–үиҝҙи·ҜеӮійҒһеҮҪж•ёдёӯд»ҚжңүдёҚз©©е®ҡзҡ„жҘөй»һпјҢеӣ жӯӨд»ҚеҸҜиғҪжңғзҷјж•ЈгҖӮ
дёІзҙҡеһӢжҲ–дәӨдә’еһӢ
еҸҰдёҖзЁ®PIDжҺ§еҲ¶еҷЁзҡ„иЎЁзӨәжі•зӮәдёІзҙҡеһӢпјҲseriesпјүжҲ–зЁұзӮәдәӨдә’еһӢпјҲinteractingпјү

е…¶дёӯеҸғж•ёе’ҢжЁҷжә–еһӢзҡ„еҸғж•ёжңүд»ҘдёӢзҡ„й—ңдҝӮ
 ,
, 

иҖҢ
 .
.
дёҠиҝ°дҪңжі•еҸҜиЎЁзӨәзӮәдәҢеҖӢдёІзҙҡзҡ„PDжҺ§еҲ¶еҷЁеҸҠPIжҺ§еҲ¶еҷЁпјҢеңЁж—©жңҹйЎһжҜ”йӣ»и·Ҝзҡ„жҷӮд»Јијғе®№жҳ“еҜҰзҸҫпјҢйӣ–然жҺ§еҲ¶еҷЁе·Із¶“ж•ёдҪҚеҢ–пјҢдёҚйҒҺд»Қжңүдәӣз¶ӯжҢҒжӯӨеҪўејҸгҖӮ
йӣўж•ЈеҢ–зҡ„жҺ§еҲ¶еҷЁ
иӢҘиҰҒеңЁеҫ®иҷ•зҗҶж©ҹпјҲMCUпјүжҲ–жҳҜFPGAдёӯеҜҰзҸҫPIDжҺ§еҲ¶жҲ–жҳҜеҲҶжһҗе…¶жҖ§иғҪпјҢе°ұйңҖиҰҒе°ҮжҺ§еҲ¶еҷЁйӣўж•ЈеҢ–[18]гҖӮдёҖйҡҺеҫ®еҲҶеҸҜд»Ҙз”ЁеҫҢеҗ‘жңүйҷҗе·®еҲҶиЎЁзӨәпјҢз©ҚеҲҶй …д№ҹйӣўж•ЈеҢ–пјҢиӢҘеҸ–жЁЈжҷӮй–“зӮә пјҢз©ҚеҲҶй …еҸҜд»Ҙз”ЁдёӢејҸиҝ‘дјј
пјҢз©ҚеҲҶй …еҸҜд»Ҙз”ЁдёӢејҸиҝ‘дјј

еҫ®еҲҶй …еҸҜиҝ‘дјјзӮә

еӣ жӯӨPIDжҺ§еҲ¶еҷЁзҡ„йӣўж•ЈеҢ–еҸҜд»Ҙе°Ү еҫ®еҲҶпјҢеҶҚз”ЁдёҖйҡҺе°Һж•ёеҸҠдәҢйҡҺе°Һж•ёзҡ„е®ҡзҫ©жұӮеҫ—
еҫ®еҲҶпјҢеҶҚз”ЁдёҖйҡҺе°Һж•ёеҸҠдәҢйҡҺе°Һж•ёзҡ„е®ҡзҫ©жұӮеҫ— пјҢеҸҜд»Ҙеҫ—еҲ°
пјҢеҸҜд»Ҙеҫ—еҲ°
![{\displaystyle u(t_{k})=u(t_{k-1})+K_{p}\left[\left(1+{\dfrac {\Delta t}{T_{i}}}+{\dfrac {T_{d}}{\Delta t}}\right)e(t_{k})+\left(-1-{\dfrac {2T_{d}}{\Delta t}}\right)e(t_{k-1})+{\dfrac {T_{d}}{\Delta t}}e(t_{k-2})\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/e71fa41e1c58fcef6f2a3a4118577458ce29c659)
е…¶дёӯ
дјӘд»Јз Ғ
д»ҘдёӢжҳҜдёҖж®өеҜҰзҸҫPIDжј”з®—жі•зҡ„дјӘд»Јз Ғпјҡ[19]
previous_error = 0
integral = 0
start:
error = setpoint - measured_value
integral = integral + error*dt
derivative = (error - previous_error)/dt
output = Kp*error + Ki*integral + Kd*derivative
previous_error = error
wait(dt)
goto start
жӯӨдҫӢдёӯжңүе…©еҖӢи®Ҡж•ёеңЁиҝҙеңҲеүҚйңҖеҲқе§ӢеҢ–зӮә0пјҢ然еҫҢй–Ӣе§ӢиҝҙеңҲгҖӮзӣ®еүҚзҡ„иӘӨе·®пјҲerrorпјүжҳҜз”Ёзӣ®еүҚзӣ®жЁҷеҖјпјҲsetpointпјүжёӣеҺ»зі»з»ҹеҸҚйҰҲеҖјпјҲmeasured_valueпјүиҖҢеҫ—пјҢ然еҫҢеҶҚйҖІиЎҢз©ҚеҲҶе’Ңеҫ®еҲҶйҒӢз®—пјҢжҜ”дҫӢй …гҖҒз©ҚеҲҶй …еҸҠеҫ®еҲҶй …д№ҳд»Ҙеҗ„иҮӘеҸғж•ёеҫҢеҫ—еҲ°ијёеҮәпјҲoutputпјүгҖӮеңЁеҜҰйҡӣзі»зөұдёӯпјҢйҖҷжңғйҖҸйҒҺж•ёдҪҚйЎһжҜ”иҪүжҸӣеҷЁиҪүжҸӣзӮәйЎһжҜ”иЁҠиҷҹпјҢдҪңзӮәеҸ—жҺ§зі»зөұзҡ„жҺ§еҲ¶йҮҸгҖӮзӣ®еүҚзҡ„иӘӨе·®йҮҸеҸҠз©ҚеҲҶжңғе„ІеӯҳпјҢд»ҘдҫҝдёӢж¬ЎиЁҲз®—еҫ®еҲҶеҸҠз©ҚеҲҶжҷӮдҪҝз”ЁпјҢзЁӢејҸжңғзӯүеҫ…dtз§’еҫҢй–Ӣе§ӢпјҢиҝҙеңҲз№јзәҢйҖІиЎҢпјҢйҖҸйҒҺйЎһжҜ”ж•ёдҪҚиҪүжҸӣеҷЁи®ҖеҸ–ж–°зҡ„зі»з»ҹеҸҚйҰҲеҖјеҸҠзӣ®жЁҷеҖјпјҢеҶҚиЁҲз®—иӘӨе·®йҮҸеҸҠијёеҮә[19]гҖӮ
еҸӮи§Ғ
жіЁйҮҠ
- ^ е”ҜдёҖзҡ„дҫӢеӨ–жҳҜзӣ®жЁҷеҖјжҒ°еҘҪжҳҜжҜ”дҫӢеўһзӣҠзӯүж–ј0жҷӮзҡ„еҸ—жҺ§ијёеҮәгҖӮ
еҸӮиҖғж–ҮзҢ®
- ^ Li, Y., Ang, K.H., and Chong, G.C.Y. (2006) Patents, software and hardware for PID control: an overview and analysis of the current art. IEEE Control Systems Magazine, 26 (1). pp. 42-54. ISSN 0272-1708 (doi:10.1109/MCS.2006.1580153)[ж°ёд№…еӨұж•ҲйҖЈзөҗ]
- ^ 2.0 2.1 2.2 Bennett, Stuart. A history of control engineering, 1930-1955. IET. 1993: p. 48. ISBN 978-0-86341-299-8.
- ^ Bennett, Stuart. Nicholas Minorsky and the automatic steering of ships (PDF). IEEE Control Systems Magazine. November 1984, 4 (4): 10вҖ“15. ISSN 0272-1708. doi:10.1109/MCS.1984.1104827. пјҲеҺҹе§ӢеҶ…е®№ (PDF)еӯҳжЎЈдәҺ2011-06-08пјү.
- ^ A Brief Building Automation History. [2011-04-04]. пјҲеҺҹе§ӢеҶ…е®№еӯҳжЎЈдәҺ2011-07-08пјү.
- ^ (Bennett 1993пјҢp. 67)
- ^ Bennett, Stuart. A brief history of automatic control (PDF). IEEE Control Systems Magazine (IEEE). 1996, 16 (3): 17вҖ“25 [2014-12-24]. пјҲеҺҹе§ӢеҶ…е®№ (PDF)еӯҳжЎЈдәҺ2016-08-09пјү.
- ^ Bennett, Stuart. A history of control engineering, 1800-1930. IET. June 1986: 142вҖ“148. ISBN 978-0-86341-047-5.
- ^ Introduction: PID Controller Design. University of Michigan. [2014-12-28]. пјҲеҺҹе§ӢеҶ…е®№еӯҳжЎЈдәҺ2012-10-23пјү.
- ^ Tim Wescott. PID without a PhD (PDF). EE Times-India. October 2000 [2014-12-28]. пјҲеҺҹе§ӢеҶ…е®№ (PDF)еӯҳжЎЈдәҺ2010-11-22пјү.
- ^ 10.0 10.1 10.2 Ang, K.H., Chong, G.C.Y., and Li, Y. (2005). PID control system analysis, design, and technology, IEEE Trans Control Systems Tech, 13(4), pp.559-576. http://eprints.gla.ac.uk/3817/1/IEEE3.pdf пјҲйЎөйқўеӯҳжЎЈеӨҮд»ҪпјҢеӯҳдәҺдә’иҒ”зҪ‘жЎЈжЎҲйҰҶпјү
- ^ Li, Y., et al. (2004) CAutoCSD - Evolutionary search and optimisation enabled computer automated control system design, Int J Automation and Computing, vol. 1, No. 1, pp. 76-88. ISSN 1751-8520. http://userweb.eng.gla.ac.uk/yun.li/ga_demo/ пјҲйЎөйқўеӯҳжЎЈеӨҮд»ҪпјҢеӯҳдәҺдә’иҒ”зҪ‘жЎЈжЎҲйҰҶпјү
- ^ Y Li, KH Ang, GCY Chong, Patents, software, and hardware for PID control: An overview and analysis of the current art, Control Systems, IEEE, 26 (1), 42-54. http://eprints.gla.ac.uk/3816/1/IEEE2pdf.pdf пјҲйЎөйқўеӯҳжЎЈеӨҮд»ҪпјҢеӯҳдәҺдә’иҒ”зҪ‘жЎЈжЎҲйҰҶпјү
- ^ Li, Y. and Ang, K.H. and Chong, G.C.Y. (2006) PID control system analysis and design - Problems, remedies, and future directions. IEEE Control Systems Magazine, 26 (1). pp. 32-41. ISSN 0272-1708 (PDF). [2014-02-02]. пјҲеҺҹе§ӢеҶ…е®№еӯҳжЎЈ (PDF)дәҺ2014-03-27пјү.
- ^ Cooper, Douglas. Integral (Reset) Windup, Jacketing Logic and the Velocity PI Form. [2014-02-18]. пјҲеҺҹе§ӢеҶ…е®№еӯҳжЎЈдәҺ2013-06-29пјү.
- ^ PID and PDFF Compensators for Motion Control (PDF). [2016-10-01]. пјҲеҺҹе§ӢеҶ…е®№ (PDF)еӯҳжЎЈдәҺ2012-09-01пјү.
- ^ Cooper, Douglas. PI Control of the Heat Exchanger. Practical Process Control by Control Guru. [2014-02-27]. пјҲеҺҹе§ӢеҶ…е®№еӯҳжЎЈдәҺ2014-02-28пјү.
- ^ Two-Degree-of-Freedom PID Controllers Mituhiko Araki and Hidefumi Taguchi (PDF). [2016-09-29]. пјҲеҺҹе§ӢеҶ…е®№еӯҳжЎЈ (PDF)дәҺ2016-09-10пјү.
- ^ Discrete PI and PID Controller Design and Analysis for Digital Implementation. Scribd.com. [2011-04-04]. пјҲеҺҹе§ӢеҶ…е®№еӯҳжЎЈдәҺ2012-01-11пјү.
- ^ 19.0 19.1 PID process control, a "Cruise Control" example. CodeProject. 2009 [4 November 2012]. пјҲеҺҹе§ӢеҶ…е®№еӯҳжЎЈдәҺ2014-12-24пјү.
еӨ–йғЁй“ҫжҺҘ
|
|---|
| й ҳеҹҹеҲҶж”Ҝ | |
|---|
| зі»зөұзү№жҖ§ | |
|---|
| ж•ёдҪҚжҺ§еҲ¶ | |
|---|
| йҖІйҡҺзҗҶи«– | |
|---|
| жҺ§еҲ¶еҷЁ | |
|---|
| жҮүз”Ё | |
|---|