数学宇宙假说
|
Read other articles:

La Convenzione sulla prescrizione nei contratti di vendita internazionale di beni mobili è un trattato preparato dalla Commissione delle Nazioni Unite per il diritto del commercio internazionale (UNCITRAL) e che completa la Convenzione sui contratti per la vendita internazionale di beni mobili (CISG). La convenzione sulla prescrizione è stata conclusa nel 1974 e poi modificata da un Protocollo adottato nel 1980 per rendere il suo testo pienamente compatibile con quello della CISG. Bibliogra...

Menggapai Ikatan CintaGenre Drama Roman Komedi PembuatVision+ OriginalsSkenario Putri Hermansjah Nicholas Raven Rojjo Suady Vanessa Gustomo Ami Murti SutradaraYogi YosePengarah kreatifWidi Lestari PutriPemeran Bella Graceva Riza Syah Shandy William Clairine Clay Neneng Risma Wulandari Yudha Ramadhan Unique Priscilla Tegar Satrya Dharty Manullang Oce Permatasari Surya Saputra Joseph L. Kara Salsa Billa Kiki Narendra Aditia Darmawan Lagu pembukaSatu Frekuensi — GovindaLagu penutupSatu Frekue...

Persekabpas PasuruanNama lengkapPerserikatan Sepakbola Kabupaten Pasuruan[1]Julukan Ajag Bromo Laskar Sakera Berdiri28 Agustus 1985StadionStadion R. SoedarsonoPogar Bangil, Kabupaten Pasuruan, Indonesia(Kapasitas: 10.000)PemilikAskab PSSI Kab. PasuruanCEO Komet SiamatManajer DR. H. Iswahyudi, M.PdPelatih SubangkitLigaLiga 3 Jawa TimurLiga 3 2018Juara 2Kelompok suporterSakeramania Kostum kandang Kostum tandang Perserikatan Sepak Bola Kabupaten Pasuruan atau Persekabpas Pasuruan adalah ...

Bowl for the infusion of tea leaves Not to be confused with Gawain. GaiwanThree gaiwan in front of a tea trayTraditional Chinese蓋碗Simplified Chinese盖碗Literal meaninglidded bowl[1]TranscriptionsStandard MandarinHanyu PinyingàiwǎnIPA[kâɪ.wàn]Alternative Chinese nameTraditional Chinese蓋杯Simplified Chinese盖杯Literal meaninglidded cupTranscriptionsStandard MandarinHanyu PinyingàibēiIPA[kâɪ.péɪ]Second alternative Chinese nameChinese焗...

Akari AsahinaAcara penandatanganan autografi di Kobe, HyogoLahir30 Mei 1988 (umur 35)Prefektur Gunma, JepangPekerjaanIdola AVTinggi5 ft 3 in (1,60 m)Situs webhttp://blog.livedoor.jp/asahina_akari/ Akari Asahina (朝日奈あかりcode: ja is deprecated , Asahina Akari, kelahiran 30 Mei 1988) adalah seorang idola AV, pemeran dan idola gravure asal Jepang. Kehidupan dan karier Lahir di Prefektur Gunma, Asahina memulai kariernya dengan video dewasa Pure white fruit yang diri...

Joseph Louis ProustLahirJoseph Louis Proust(1754-09-26)26 September 1754Meninggal5 Juli 1826(1826-07-05) (umur 71)Angers, PrancisPekerjaanKimiawan Joseph Louis Proust (26 September 1754 – 5 Juli 1826) adalah seorang aktor dan kimiawan Prancis. Ia paling dikenal karena menemukan hukum komposisi konstan pada 1799. Kehidupan Joseph L. Proust lahir pada 26 September 1754 di Angers, Prancis Pada 5 Juli 1826 ia meninggal di Angers, Prancis. Pranala luar Wikisource memiliki teks artikel Ensi...

Salamander punggung merah Status konservasi Risiko Rendah (IUCN 3.1) Klasifikasi ilmiah Kerajaan: Animalia Filum: Chordata Kelas: Amphibia Ordo: Caudata Famili: Plethodontidae Genus: Plethodon Spesies: P. cinereus Nama binomial Plethodon cinereus(Hijau, 1818) Salamander punggung merah (Plethodon cinereus) adalah salamander hutan kecil. Hewan ini mendiami lereng berhutan di Amerika Utara sisi timur; yaitu ke barat hingga Missouri; selatan hingga Carolina Utara; dan utara dari Quebe...

Roller derby league Sacramento Roller DerbyMetro areaSacramento, CACountryUnited StatesFounded2006Track type(s)FlatVenueThe RinkAffiliationsWFTDAWebsitesacramentorollerderby.com Sacramento Roller Derby is a women's flat track roller derby league based in Sacramento, California. Originally two separate leagues founded in 2006, Sac City Rollers and Sacred City Derby Girls, who mutually announced a pending merger in late 2017, and then on January 1, 2018, announced a rebrand of the merged organi...

Il territorio dei Paesi Bassi avvolto dai colori della bandiera arcobaleno. I diritti LGBT nei Paesi Bassi sono pienamente riconosciuti e applicati, essendo uno dei paesi più progressisti al mondo in materia di trattamento paritario nei confronti dei propri cittadini lesbiche, gay, bisessuali e transgender (LGBT). Gli atti omosessuali sono stati legalizzati nel 1811, dopo che il primo impero francese invase il paese installando il codice Napoleonico e cancellando in tal modo tutte le precede...

Begging for LoveSampul DVD untuk Begging for Love (1998)SutradaraHideyuki Hirayama[1]ProduserTadamichi AbeSadatoshi FujimineHideyuki TakaiDitulis olehHarumi Shimoda (novel)Wui Sin Chong (permainan latar)PemeranMieko HaradaSinematograferKozo ShibazakiPenyuntingAkimasa KawashimaDistributorTohoTanggal rilis 26 September 1998 (1998-09-26) Durasi135 menitNegaraJepangBahasaJepang Begging for Love (愛を乞うひとcode: ja is deprecated , Ai o Kou Hito) adalah sebuah film Jepang 1998 ...

Refia SultanSultana dell'impero ottomano TrattamentoSua Altezza Imperiale NascitaIstanbul, 15 giugno 1881 MorteBeirut, 1938 Luogo di sepolturaMonastero di Solimano, Damasco, Siria DinastiaCasa di Osman PadreAbdülhamid II MadreSazkar Hanım ConiugeAli Fuad Bey(1910-1938) FigliRabia HanımsultanAyşe Hamide Hanımsultan ReligioneIslam sunnita Refia Sultan (turco ottomano: رفیعه سلطان, colei che ascende; Istanbul, 15 giugno 1891 – Beirut, 1938) è stata una principessa ottomana...

American author and lecturer (born 1957) This article is about the progressive education proponent. For the authority on government deregulation, see Alfred E. Kahn. Alfie KohnBorn (1957-10-15) October 15, 1957 (age 66)Miami Beach, Florida, U.S.EducationBrown University (B.A.)University of Chicago (M.A.)Occupation(s)Author and lecturer (education, psychology, and parenting) Alfie Kohn (born October 15, 1957) is an American author and lecturer in the areas of education, parenting, and hum...

Panzerwurfmine (Lang) Allgemeine Angaben Bezeichnung: Panzerwurfmine (Lang) Typ: Hohlladung Herkunftsland: Deutsches Reich Indienststellung: 1943 Einsatzzeit: 1943–1945 Technische Daten Gefechtsgewicht: 1,36 kg Ladung: 500 g RDX und TNT Länge: 533 mm Listen zum Thema Die Panzerwurfmine (Lang) war ein Panzernahbekämpfungsmittel der Wehrmacht, das im Zweiten Weltkrieg eingesetzt wurde. Sie erinnerte in Aufbau und Einsatzweise an eine Stielhandgranate, trug aber eine Hohlladung zur Panzerbe...
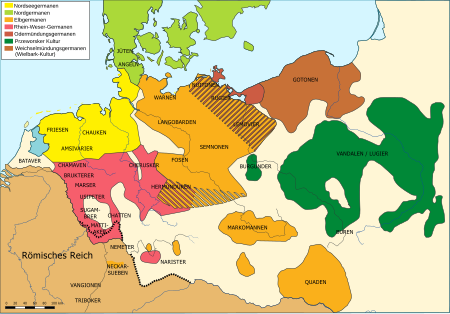
Херу́ски (нем. Cherusker, лат. Cherusci, греч. Χηρούσκοι, Χαιρουσκοί) — древнегерманское племя, относящееся к восточной группе древнегерманских племён. Расселение германских племён в 50 году н. э.; херуски (CHERUSKER) — в ареале обитания племён Рейна-Везера (выделен розовым) Со...

The Act of Abolition of Slavery in Tunisia in 1846. Part of a series onForced labour and slavery Contemporary Child Labour Child soldiers Conscription Debt Forced marriage Bride buying Child marriage Wife selling Forced prostitution Human trafficking Peonage Penal labour Contemporary Africa 21st-century jihadism Sexual slavery Wage slavery Historical Antiquity Egypt Babylonia Greece Rome Medieval Europe Ancillae Black Sea slave trade Byzantine Empire Kholop Prague slave trade Serfs History I...

Styles of Romanesque architecture developed by the NormansThis article has multiple issues. Please help improve it or discuss these issues on the talk page. (Learn how and when to remove these messages) This article needs additional citations for verification. Please help improve this article by adding citations to reliable sources. Unsourced material may be challenged and removed.Find sources: Norman architecture – news · newspapers · books · scholar �...

Pour les articles homonymes, voir Gouvernement Tymochenko. Gouvernement Tymochenko I Ukraine Données clés Président Viktor Iouchtchenko Premier ministre Ioulia TymochenkoIouriï Iekhanourov a.i. Élection 31 mars 2002 Formation 4 février 2005 Fin 28 septembre 2005 Durée 7 mois et 24 jours Composition initiale Coalition BIouT-BNU-SPU-PPPU Ministres 22 Représentation Rada 162 / 450 Ianoukovytch I Iekhanourov modifier - modifier le code - voir Wikidata (aide) Le gouv...

For his grandson, see Prince Ferdinando, Duke of Genoa (1884–1963). Duke of Genoa Prince FerdinandoPainting of Prince FerdinandDuke of GenoaTenure27 April 1831 – 10 February 1855PredecessorCarlo FeliceSuccessorTommasoBorn(1822-11-15)15 November 1822Florence, Grand Duchy of TuscanyDied10 February 1855(1855-02-10) (aged 32)Turin, Kingdom of SardiniaSpouse Princess Elisabeth of Saxony (m. 1850)Issue Margherita, Queen of Italy Prince Tommaso, Duke o...

Former Filipino convict For the English cricketer, see Hubert Webb (cricketer). In this Philippine name, the middle name or maternal family name is Pagaspas and the surname or paternal family name is Webb. Hubert WebbBornHubert Jeffrey Pagaspas Webb (1968-11-07) November 7, 1968 (age 55)San Diego, California, U.S.Spouse Cecille Perez (m. 2016)Children1 Hubert Jeffrey Pagaspas Webb (born November 7, 1968), is the third son of Freddie Webb, as well a...

Individual who is known and addressed by a single name A mononym is a name composed of only one word. An individual who is known and addressed by a mononym is a mononymous person. A mononym may be the person's only name, given to them at birth. This was routine in most ancient societies, and remains common in modern societies such as in Afghanistan,[1] Bhutan, Indonesia (especially by the Javanese), Myanmar, Mongolia, Tibet,[2] and South India. In other cases, a person may sel...

