![]() еВЕзІСжУЇ
еВЕзІСжУЇ
 йРШжУЇеОЯзРЖ
йРШжУЇеОЯзРЖ
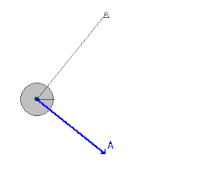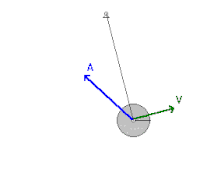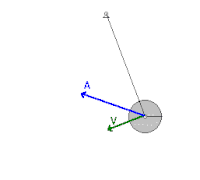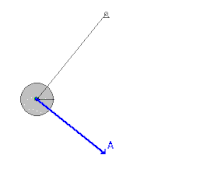
жУЇжШѓдЄАз®Ѓеѓ¶й©ЧеДАеЩ®пЉМеПѓзФ®дЊЖе±ХзПЊз®Ѓз®ЃеКЫе≠ЄзПЊи±°гАВжЬАеЯЇжЬђзЪДжУЇзФ±дЄАжҐЭзє©жИЦзЂњпЉМеТМдЄАеАЛйМШзµДжИРгАВйМШзєЂеЬ®зє©зЪДдЄЛжЦєпЉМзє©зЪДеП¶дЄАзЂѓеЫЇеЃЪгАВзХґжО®еЛХжУЇжЩВпЉМйМШдЊЖеЫЮзІїеЛХгАВжУЇеПѓдї•дљЬдЄАеАЛи®ИжЩВеЩ®гАВ
й°ЮеЮЛ
з∞°иЂІйБЛеЛХ
иЛ•жЬАйЂШиЩХпЉИ  пЉЙзЪДзє©е≠РеТМжЬАдљОиЩХпЉИйАЯеЇ¶жЬАе§ІеАЉпЉЙзЪДзє©е≠РзЪДиІТеЇ¶зВЇ
пЉЙзЪДзє©е≠РеТМжЬАдљОиЩХпЉИйАЯеЇ¶жЬАе§ІеАЉпЉЙзЪДзє©е≠РзЪДиІТеЇ¶зВЇ  пЉМзђ¶еРИпЉЪ
пЉМзђ¶еРИпЉЪ

еЙЗеПѓдљњзФ®дЄЛеИЧеЕђеЉПзЃЧеЗЇеЃГзЪДжМѓеЛХйА±жЬЯгАВ
йА±жЬЯеЕђеЉП
 пЉИ
пЉИ  зВЇжУЇйХЈпЉЫ
зВЇжУЇйХЈпЉЫ  зВЇзХґеЬ∞йЗНеКЫеК†йАЯеЇ¶пЉЙ
зВЇзХґеЬ∞йЗНеКЫеК†йАЯеЇ¶пЉЙ
дЄАжУЇйХЈзВЇ  еЕђе∞ЇзЪДеЦЃжУЇпЉМжЦЉеЬ∞и°®иЩХдљЬе∞ПиІТеЇ¶жУЇеЛХеПѓињСдЉЉзВЇз∞°иЂІйБЛеЛХпЉМйА±жЬЯ
еЕђе∞ЇзЪДеЦЃжУЇпЉМжЦЉеЬ∞и°®иЩХдљЬе∞ПиІТеЇ¶жУЇеЛХеПѓињСдЉЉзВЇз∞°иЂІйБЛеЛХпЉМйА±жЬЯ  пЉМйАЩз®ЃеЦЃжУЇз®±дєЛзВЇзІТжУЇгАВ
пЉМйАЩз®ЃеЦЃжУЇз®±дєЛзВЇзІТжУЇгАВ
еЕђеЉПи≠ЙжШО
дЄАеЦЃжУЇжУЇйМШж≠£еЬ®жУЇзЫ™жЬАйЂШиЩХ(ж≠§жЩВ  )пЉМзє©еТМйЙЫзЫізЈЪжЬЙе§ЊиІТ
)пЉМзє©еТМйЙЫзЫізЈЪжЬЙе§ЊиІТ  пЉМзє©йХЈзВЇ
пЉМзє©йХЈзВЇ  пЉМзЫЄе∞НжЦЉеє≥и°°йїЮзЪДдљНзІїзВЇ
пЉМзЫЄе∞НжЦЉеє≥и°°йїЮзЪДдљНзІїзВЇ 
ж≠§зЙ©йЂФеПЧдЄЛеИЧеКЫзЪДељ±йЯњпЉИдЄЛеИЧи™™жШОй̃虧пЉМзє©е≠РзЪДеЉµеКЫжШѓеЫ†зВЇжУЇйМШйЗНеКЫеЉХиµЈпЉМдїїдљХдЄАзЮђйЦУжУЇйМШж≥ХеРСпЉИеЊСеРСпЉЙеРИеКЫзВЇйЫґпЉМдљЖеИЗзЈЪеК†йАЯеЇ¶зВЇ  пЉЙ
пЉЙ
- зє©е≠РдєЛжЛЙеКЫе§Іе∞П

- йЗНеКЫе§Іе∞П

зє©е≠РзЪДжЛЙеКЫ  жЬЙеИЖеКЫ
жЬЙеИЖеКЫ





иІ£еЊЧ 
дї£еЕ• 
еЊЧеИ∞ 
ж†єжУЪеї£зЊ©зЫЄе∞НиЂЦеПѓзЯ•пЉМ
жХЕ 
еЦЃжУЇ

 sin ќЄ еПЦзВЇќЄзЪД虧壁гАВ
sin ќЄ еПЦзВЇќЄзЪД虧壁гАВ

гАМ
еНХжСЖгАНйЗНеЃЪеРСиЗ≥ж≠§гАВ
еПЦ  зВЇзє©зЪДйХЈеЇ¶пЉМ
зВЇзє©зЪДйХЈеЇ¶пЉМ  зВЇзє©еТМеЮВзЫіеє≥йЭҐзЪДзЈЪзЪДдЇ§иІТпЉМ
зВЇзє©еТМеЮВзЫіеє≥йЭҐзЪДзЈЪзЪДдЇ§иІТпЉМ зВЇ
зВЇ  зЪДжЬАе§ІеАЉпЉМ
зЪДжЬАе§ІеАЉпЉМ зВЇйМШзЪДи≥™йЗПпЉМ
зВЇйМШзЪДи≥™йЗПпЉМ и°®з§ЇиІТеЇ¶еК†йАЯеЇ¶
и°®з§ЇиІТеЇ¶еК†йАЯеЇ¶  гАВ
гАВ
ењљзХ•з©Їж∞£йШїеКЫдї•еПКзє©зЪДељИжАІгАБйЗНйЗПзЪДељ±йЯњпЉЪ
- йМШйАЯзОЗжЬАйЂШжШѓеЬ®
 жЩВгАВзХґйМШеНЗеИ∞жЬАйЂШйїЮпЉМеЕґйАЯзОЗзВЇ 0гАВзє©зЪДеЉµеКЫж≤ТжЬЙе∞НйМШеБЪеКЯпЉМжХіеАЛйБОз®ЛдЄ≠еЛХиГљеТМдљНиГљзЪДеТМдЄНиЃКпЉМж©ЯжҐ∞иГљеЃИжБЖгАВ
жЩВгАВзХґйМШеНЗеИ∞жЬАйЂШйїЮпЉМеЕґйАЯзОЗзВЇ 0гАВзє©зЪДеЉµеКЫж≤ТжЬЙе∞НйМШеБЪеКЯпЉМжХіеАЛйБОз®ЛдЄ≠еЛХиГљеТМдљНиГљзЪДеТМдЄНиЃКпЉМж©ЯжҐ∞иГљеЃИжБЖгАВ
- йБЛеЛХжЦєз®ЛзВЇпЉЪ

ж≥®жДПеИ∞дЄНиЂЦќЄзЪДеАЉзВЇдљХпЉМйБЛеЛХйА±жЬЯеТМйМШзЪДи≥™йЗПзД°йЧЬгАВ
зХґ  зЫЄзХґе∞ПзЪДжЩВеАЩпЉМ
зЫЄзХґе∞ПзЪДжЩВеАЩпЉМ пЉМеЫ†ж≠§еПѓеЊЧеИ∞дЄАжҐЭдЇМйЪОйљКжђ°еЄЄдњВжХЄеЊЃеИЖжЦєз®ЛгАВж≠§зВЇдЄАз∞°иЂІйБЛеЛХпЉМйА±жЬЯ
пЉМеЫ†ж≠§еПѓеЊЧеИ∞дЄАжҐЭдЇМйЪОйљКжђ°еЄЄдњВжХЄеЊЃеИЖжЦєз®ЛгАВж≠§зВЇдЄАз∞°иЂІйБЛеЛХпЉМйА±жЬЯ  гАВ
гАВ
жЇЦ祯зЪДйБЛеЛХйА±жЬЯдЄНеПѓдї•зФ®еЯЇз§ОеЗљжХЄж±ВеЊЧгАВиАГжЕЃеЊЃеИЖжЦєз®ЛпЉЪ



е∞ЗдЄКеЉПйЗНеѓЂжИРзђђдЄАй°Юж©ҐеЬУеЗљжХЄзЪД嚥еЉПпЉЪ

еЕґдЄ≠
йА±жЬЯеПѓдї•зФ®зіЪжХЄи°®з§ЇжИРпЉЪ
![{\displaystyle T=2\pi {\sqrt {L \over {\mathrm {g} }}}\left[1+\left({\frac {1}{2}}\right)^{2}\sin ^{2}{\frac {\theta _{0}}{2}}+\left({\frac {1\cdot 3}{2\cdot 4}}\right)^{2}\sin ^{4}{\frac {\theta _{0}}{2}}+\left({\frac {1\cdot 3\cdot 5}{2\cdot 4\cdot 6}}\right)^{2}\sin ^{6}{\frac {\theta _{0}}{2}}+\cdots \right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/89530b6d177974d59c72066989d56d5a339d1442)
![{\displaystyle =2\pi {\sqrt {\frac {L}{g}}}\left(1+{\frac {1}{16}}\theta _{0}^{2}+{\frac {11}{3072}}\theta _{0}^{4}+\cdots \right)=2\pi {\sqrt {\frac {L}{g}}}\left[\sum _{n=0}^{\infty }\left({\frac {\left(2n\right)!}{2^{2n}\left(n!\right)^{2}}}\right)^{2}\sin ^{2n}\left({\frac {\theta _{0}}{2}}\right)\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/5bc6b231c69b842d48ad60dc442655ae5e41603d)
и°ЭжУКжУЇ

и°ЭжУКжУЇжШѓдЊЖзФ®и®ИзЃЧе≠РеЉєйАЯеЇ¶зЪДеѓ¶й©ЧеЃ§еДАеЩ®гАВеЃГзЪДеОЯзРЖзВЇпЉЪзЙ©дїґзҐ∞жТЮеЙНеЊМеЛХйЗПеЃИжБТпЉМжУЇйБЛеЛХжЩВиГљйЗПеЃИжБТгАВ
и°ЭжУКжУЇеТМжЩЃйАЪжУЇзЫЄдЉЉпЉМзЙєеИ•дєЛиЩХеЃГзЪДйМШжЬГеТМе∞ДеЕ•е≠РеЉєзФҐзФЯеЃМеЕ®йЭЮељИжАІзҐ∞жТЮпЉМеН≥зҐ∞жТЮеЊМеЕ©иАЕжЬГеРИзВЇдЄАгАВ
е∞Зе≠РеЉєе∞ДеРСеБЬж≠ҐзЪДйМШпЉМдљњйМШеТМе≠РеЉєеРИеЬ®дЄАиµЈжУЇеЛХгАВи®≠йМШи≥™йЗПзВЇ пЉМе≠РеЉєи≥™йЗПеТМеИЭйАЯеЇ¶еИЖеИ•зВЇ
пЉМе≠РеЉєи≥™йЗПеТМеИЭйАЯеЇ¶еИЖеИ•зВЇ еТМvпЉМйМШеТМе≠РеЉєзҐ∞жТЮеЊМзЪДйАЯеЇ¶зВЇuгАВ
еТМvпЉМйМШеТМе≠РеЉєзҐ∞жТЮеЊМзЪДйАЯеЇ¶зВЇuгАВ
дї•дЄЛжШѓе≠РеЉєйАЯеЇ¶зЪДи®ИзЃЧжЦєж≥ХпЉЪ
зФ±еЛХйЗПеЃИжБТеЃЪеЊЛпЉМ

зФ±иГљйЗПеЃИжБТеЃЪеЊЛпЉМ

иІ£еЊЧ  гАВ
гАВ
еАТеЦЃжУЇ
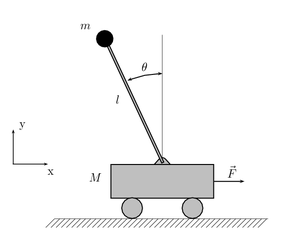 еТМеП∞иїКеТМеАТеЦЃжУЇзµДжИРзЪДз≥їзµ±
еТМеП∞иїКеТМеАТеЦЃжУЇзµДжИРзЪДз≥їзµ±
еАТеЦЃжУЇжЬЙи®±е§ЪдЄНеРМзЪДжЮґжІЛпЉМеЄЄи¶ЛзЪДжЬЙдЇМз®ЃгАВ
жЬАз∞°еЦЃзЪДжШѓзД°и≥™йЗПзЪДзЫіж°њдЄАзЂѓжО•еЬ®еЫЇеЃЪзЪДж®ЮзіРдЄКпЉМеП¶дЄАзЂѓйА£зµРйЗНйЗПпЉМж≠§жЮґжІЛй°ЮдЉЉдЄАиИђеЦЃжУЇпЉМдљЖеЫ†зВЇйЗНйЗПеЬ®ж®ЮзіРйїЮдЄКжЦєпЉМзЫіж°њеЬ®йЗНйЗПдЄЛжЦєпЉМйЬАжФѓжМБйЗНзЙ©дЄНиРљдЄЛпЉМеЫ†ж≠§жЬГе∞ЗеЦЃжУЇзЪДзЈЪжФєзВЇжЬЙеЙЫжАІзЪДзЫіж°њгАВ
еП¶е§ЦдЄАз®ЃжШѓе∞ЗеАТеЦЃжУЇжФЊеЬ®еПѓдї•дЄАзґ≠ж∞іеє≥йБЛеЛХзЪДеП∞иїКдЄКпЉМйАПйБОеП∞иїКзЪДж∞іеє≥йБЛеЛХдЊЖжОІеИґжУЇзЪДдљНзљЃгАВ
еАТеЦЃжУЇеЬ®жУЇзЫізЂЛжЬЭдЄКжЩВеПѓдї•еє≥и°°пЉМдЄНйБОжШѓдЄНз©©еЃЪеє≥и°°пЉМйЬАи¶БйАПйБОжОІеИґз≥їзµ±жЙНиГљзґ≠жМБеє≥и°°гАВ
еЬЖйМРжУЇ
йМРжУЇзЪДиЈѓеЊСжШѓеє≥йЭҐдЄКеЬУгАВжУЇйБЛеЛХжЩВпЉМзє©зЪДиЈѓеЊСзВЇдЄАеАЛеЬУйМРйЭҐгАВйАЩжШѓеЬУеС®йБЛеЛХгАВ
и§ЗжУЇпЉИзЙ©зРЖжУЇ/compound pendulum)

гАМ
е§НжСЖгАНйЗНеЃЪеРСиЗ≥ж≠§гАВ
зХґи≥™йЗПдЄНйЫЖдЄ≠жИЦдЄНи¶ПеЙЗзЪДзЙ©йЂФдї•иљЙиїЄеРКиµЈжУЇеЛХжЩВпЉМж≠§жУЇз®±дљЬи§ЗжУЇпЉИзЙ©зРЖжУЇпЉЙгАВзФ±жЦЉжЬЙи≥™йЗПеИЖдљИзЪДзЈ£жХЕпЉМйА±жЬЯиЈЯеЙЫжАІзЙ©йЂФйЗНењГе∞НиљЙиїЄзЪДиљЙеЛХжЕ£йЗПпЉИIпЉЙжЬЙйЧЬгАВж†єжУЪеє≥и°МиїЄеЃЪзРЖеПКеПѓдї•ж±ВеЗЇе∞ПиІТеЇ¶и§ЗжУЇйА±жЬЯзВЇ 
йЫЩжУЇ(complex pendulum/double pendulum)
 йЫЩжУЇз≥їзµ±зЪДдЄАдЊЛ
йЫЩжУЇз≥їзµ±зЪДдЄАдЊЛ
йЫЩжУЇз≥їзµ±жШѓжЈЈж≤МзЪДгАВ
з£БжАІжУЇ
еТМйЫЩжУЇдЄАж®£пЉМз£БжАІжУЇз≥їзµ±жШѓжЈЈж≤МзЪДгАВ
жЗЙзФ®
еВЕзІСжУЇ
еВЕзІСжУЇзЪДзІїеЛХеПѓдљЬзВЇеЬ∞зРГиЗ™иљЙзЪДи≠ЙжУЪгАВ
йРШжУЇ
жУЇйРШгАВ
зВЇдЇЖжЄЫе∞СжЇЂеЇ¶иЃКеМЦзЪДељ±йЯњпЉМжЬЙдЄНеРМзЪДи®≠и®ИпЉЪ
- жߵ嚥и£ЬеДЯжУЇпЉИGridiron PendulumпЉЙпЉЪдї•дЄНеРМйЗСе±ђпЉИйЛЉеТМйКЕпЉЙйЕНжР≠пЉМдњЭжМБжУЇзЪДйХЈеЇ¶дЄНиЃК[1]
- Graham's pendulumпЉЪжЬЙдЄАеАЛж∞ійКАзЃ°жЯ±пЉМдњЭжМБжУЇзЪДйЗНењГдЄНиЃК
- дї•жЬ®и£љжУЇ[2]
- Ellicott compensated pendulumпЉЪзФ®е§ЪеАЛжУЇзЪДзµРжІЛйЕНеРИ
еПГиАГ
- Paul Appell, "Sur une interprétation des valeurs imaginaires du temps en Mécanique", Comptes Rendus Hebdomadaires des Scéances de l'Académie des Sciences, volume 87, number 1, July, 1878.
- The Pendulum: A Physics Case Study, Gregory L. Baker and James A. Blackburn, Oxford University Press, 2005
- ^ [1] пЉИй°µйЭҐе≠Шж°£е§ЗдїљпЉМе≠ШдЇОдЇТиБФзљСж°£ж°Ий¶ЖпЉЙ
- ^ [2] пЉИй°µйЭҐе≠Шж°£е§ЗдїљпЉМе≠ШдЇОдЇТиБФзљСж°£ж°Ий¶ЖпЉЙ