Read other articles:

Sir Gaëtan Duval AirportIATA: RRGICAO: FIMRInformasiJenisPublicPengelolaAirport of Rodrigues Ltd - Licensed Aerodrome OperatorLokasiPlaine Corail, Rodrigues, MauritiusKetinggian dpl29 mdplKoordinat19°45′27″S 063°21′39″E / 19.75750°S 63.36083°E / -19.75750; 63.36083Landasan pacu Arah Panjang Permukaan m kaki 12/30 1,020 3,346 Aspal Source: DAFIF[1][2] Bandar Udara Pulau Rodrigues merupakan sebuah bandar udara yang terletak di Pulau...

Malayan-Singaporean badminton player In this Malay name, there is no surname or family name. The name Marjan is a patronymic, and the person should be referred to by their given name, Ismail. Badminton playerIsmail MarjanIsmail Marjan in 1949Personal informationNickname(s)Pak Mail[1]Birth nameIsmail bin Haji MarjanCountrySingaporeBorn(1920-06-07)7 June 1920[1]British MalayaDied25 January 1991(1991-01-25) (aged 70)[2]SingaporeHandednessRight Medal record Men's...

Orang Ekuador EcuatorianosBendera Ekuador; simbol persatuan orang EkuadorJumlah populasic. 18,5 juta(Diaspora) c. 1,5 jutaDaerah dengan populasi signifikan Ekuador 0 juta (est. 2018)[1][2] Amerika Serikat717,995[3] Spanyol444,347 [4][5] Italia66,590[6] Chili42,022[7] Kanada25,410[8] Jerman16,000[9] Kolombia11,404[10] Prancis10,249[11] Britania Raya9,42...

Patung dada Nefertiti yang berada di Museum Altes Berlin. Nefertiti (kecantikan telah datang) adalah Permaisuri Agung (atau istri utama) dari Fir'aun/Pharaoh Amenhotep IV (kemudian bergelar Akhenaten), dan merupakan ibu mertua dan mungkin ibu tiri dari Pharaoh Tutankhamun. Ia juga kemungkinan memerintah kerajaan dalam waktu singkat dengan nama Neferneferuaten-Nefertiti (berarti, Aten memancarkan sinarnya karena Kecantikan telah datang) setelah suaminya meninggal dan sebelum bertahtanya Tutank...

Questa voce o sezione sull'argomento vescovi tedeschi non cita le fonti necessarie o quelle presenti sono insufficienti. Puoi migliorare questa voce aggiungendo citazioni da fonti attendibili secondo le linee guida sull'uso delle fonti. Johann Ludwig von Elderenvescovo della Chiesa cattolica  Incarichi ricopertiVescovo di Liegi (1688-1694)  Nato29 settembre 1620 Ordinato diacono16 marzo 1669 Ordinato presbitero10 febbraio 1670 Nominato vescovo15 novembre 1688 da papa Innocenzo...

Cricket tournament 2019–20 Ranji Trophy Group AThe Ranji Trophy, awarded to the winnersDates9 December 2019 (2019-12-09) – 15 February 2020 (2020-02-15)Administrator(s)BCCICricket formatFirst-class cricketTournament format(s)Round-robinHost(s) IndiaParticipants9← 2018–19 2019–20 Indian domestic cricket season Men Duleep Trophy Vijay Hazare Trophy (Group A, Group B, Group C, Plate Group) Deodhar Trophy Syed Mushtaq Ali Trophy (Group A, Group B, ...

NgrayunKecamatanPeta lokasi Kecamatan NgrayunNegara IndonesiaProvinsiJawa TimurKabupatenPonorogoPemerintahan • Camat-Populasi • Total56.760 jiwaKode Kemendagri35.02.02 Kode BPS3502010 Luas184,76 km²[1]Desa/kelurahan11 Ngrayun adalah sebuah kecamatan di Kabupaten Ponorogo, Provinsi Jawa Timur, Indonesia. Kecamatan ini berjarak sekitar 30 kilometer[2] dari ibu kota Kabupaten Ponorogo ke arah selatan. Pusat pemerintahannya berada di desa Ngrayun. Kec...

English footballer Jack Powell Powell in November 2015Personal informationFull name Jack Patrick Powell[1]Date of birth (1994-01-29) 29 January 1994 (age 30)[2]Place of birth Canning Town, EnglandHeight 1.85 m (6 ft 1 in)[2]Position(s) MidfielderTeam informationCurrent team Crewe AlexandraNumber 23Youth career0000–2013 West Ham UnitedSenior career*Years Team Apps (Gls)2013–2016 Millwall 6 (0)2013–2014 → Concord Rangers (loan) 7 (1)2015–201...

Short period of the most exceptional artistic production during the Italian Renaissance Raphael's frescos in the Raphael Rooms of the Apostolic Palace in the Vatican, also commissioned by Pope Julius II The Creation of Adam, a scene from Michelangelo's Sistine Chapel ceiling (c. 1508–1512), commissioned by Pope Julius II The Last Supper, mural painting by Leonardo da Vinci In art history, the High Renaissance was a short period of the most exceptional artistic production in the Italian stat...

Meccanismi dell'epigenetica L'epigenetica (dal greco ἐπί, epì, «sopra» e γεννητικός, gennitikòs, «relativo all'eredità familiare») è una branca della genetica[1] che si occupa dei cambiamenti fenotipici ereditabili da una cellula o un organismo, in cui non si osserva una variazione del genotipo[2]. È stata definita da Arthur Riggs e colleghi come lo studio dei cambiamenti mitotici e meiotici ereditabili che non possono essere spiegati tramite modific...

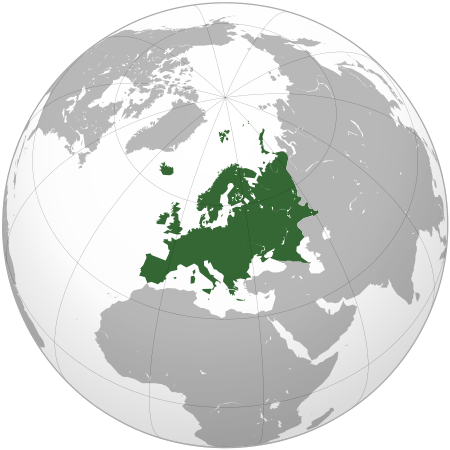
La Lituanie est une république parlementaire régie par la Constitution du 25 octobre 1992. Pouvoir exécutif Le Président de la République de Lituanie est élu au suffrage universel direct pour cinq ans. La Constitution Lituanienne dispose en outre que nul ne peut être élu Président de la République plus de deux fois consécutives. Le Premier ministre est nommé et révoqué par le Président avec l'approbation du Seimas, le Parlement lituanien. Les ministres sont nommés et relevés ...

Dunning Mountain2016 Landsat image of Dunning MountainHighest pointElevation2,146 ft (654 m)[1]Coordinates40°14′44″N 78°26′46″W / 40.2456°N 78.4461°W / 40.2456; -78.4461GeographyLocationPennsylvania, U.S.Parent rangeAppalachian MountainsTopo mapUSGS New Enterprise (PA) Quadrangle and Roaring Spring (PA) Quadrangle Dunning Mountain is a stratigraphic ridge in central Pennsylvania, United States. The mountain's north end is at McKee Gap...

Addis Abeba-GibutiStati attraversati Gibuti Etiopia InizioAddis Abeba FineGibuti Attivazione1917 Soppressione1941 Riattivazione1944 GestoreEthio-Djibouti Railways(Chemin de fer Ethio-Dijboutien) Precedenti gestoriImperial Railway Company of EthiopiaCompagnie de Chemin de fer de Somalie FrançaiseFerrovie Etiopiche Lunghezza784 km Scartamento1000 mm Elettrificazioneno Ferrovie Modifica dati su Wikidata · Manuale La ferrovia Addis Abeba-Gibuti è una linea ferroviaria in di...

此條目需要补充更多来源。 (2021年7月4日)请协助補充多方面可靠来源以改善这篇条目，无法查证的内容可能會因為异议提出而被移除。致使用者：请搜索一下条目的标题（来源搜索：美国众议院 — 网页、新闻、书籍、学术、图像），以检查网络上是否存在该主题的更多可靠来源（判定指引）。 美國眾議院 United States House of Representatives第118届美国国会众议院徽章 众议院旗...

Icelandic online newspaper KjarninnFormatOnline newspaperFoundedAugust 23, 2013; 10 years ago (2013-08-23)LanguageIcelandicCeased publicationJanuary 13, 2023; 17 months ago (2023-01-13)HeadquartersReykjavík, IcelandWebsitewww.kjarninn.is Kjarninn (lit. 'the core') was an Icelandic online newspaper founded in August 2013. Previously Kjarninn was a weekly digital news magazine served via Apple App Store aimed at tablet computer users but PDFs were also...

American politician from Vermont Christopher A. BrayBray in 2019Member of the Vermont Senatefrom the Addison districtIncumbentAssumed office January 9, 2013Serving with Claire Ayer (2013-2019) Ruth Hardy (2019-Present)Preceded byHarold GiardMember of the Vermont House of Representativesfrom the Addison-5 districtIn officeJanuary 2007 – January 2011Preceded byHarvey T. SmithSucceeded byHarvey T. Smith Personal detailsBornJune 29, 1955New Britain, ConnecticutN...

La Grande Palestine[1] (arabe: فلسطين الكبرى) est une notion irrédentiste utilisée par certains nationalistes palestiniens cherchant à établir un État-nation palestinien sur l'ensemble de l'ancienne Palestine sous mandat (l'actuel État d'Israël, la Cisjordanie et la bande de Gaza) voire de l'Émirat de Transjordanie. Certains responsables de l'Organisation de libération de la Palestine ont étendu les revendications des années 1970 et 1980 à la Jordanie. Le terme est con...

Tajikistan Artikel ini adalah bagian dari seri Politik dan KetatanegaraanTajikistan Konstitusi Hak asasi manusia Pemerintahan Presiden Emomalii Rahmon Perdana Menteri Kokhir Rasulzoda Legislatif Majelis Tertinggi Majelis Nasional Majelis Perwakilan Pemilihan umum Recent elections Presiden: 20062013 Parlemen: 200520102015 Partai politik Pembagian administratif Provinsi Distrik Jamoat Hubungan luar negeri Negara lainnya Atlas lbs Konstitusi Tajikistan diadopsi pada tanggal 6 November 1994 dan d...

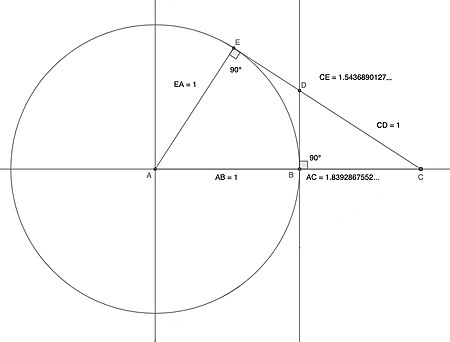
Mathematical sequences In mathematics, the Fibonacci numbers form a sequence defined recursively by: F n = { 0 n = 0 1 n = 1 F n − 1 + F n − 2 n > 1 {\displaystyle F_{n}={\begin{cases}0&n=0\\1&n=1\\F_{n-1}+F_{n-2}&n>1\end{cases}}} That is, after two starting values, each number is the sum of the two preceding numbers. The Fibonacci sequence has been studied extensively and generalized in many ways, for example, by starting with other numbers than 0 and 1, by ad...

Клини́ческая психоло́гия (медици́нская психоло́гия[1][2]) — раздел психологии (на стыке с медициной), изучающий психические явления с точки зрения их взаимосвязи с болезнями. Сфера клинической психологии включает в себя диагностику психического здоровья, орга...