Read other articles:

Artikel ini terlalu bergantung pada referensi dari sumber primer. Mohon perbaiki artikel ini dengan menambahkan sumber sekunder atau tersier. (Pelajari cara dan kapan saatnya untuk menghapus pesan templat ini) Universitas Sunan Giri SurabayaDidirikan1960RektorDr. H. Didit Darmawan, S.T., S.E., M.MAlamatJl. Brigjen Katamso II, Kedungrejo, Waru, Kabupaten Sidoarjo, Jawa Timur 61256 Situs webunsuri.ac.id Universitas Sunan Giri Surabaya (UNSURI Surabaya) merupakan perguruan tinggi keagamaan islam...

Summer Time Renderingサマータイムレンダ(Samā Taimu Renda)GenreMisteriSupernatural[1]Cerita seru[2] MangaPengarangYasuki TanakaPenerbitShueishaPenerbit bahasa InggrisNA Udon EntertainmentImprintJump Comics+MajalahShōnen Jump+DemografiShōnenTerbit23 Oktober, 2017 – 1 Februari, 2021Volume13 Seri animeSutradaraAyumu WatanabeSkenarioHiroshi SekoMusikKeiichi OkabeRyuichi TakadaKeigo HoashiStudioOLMPelisensiDisney Platform DistributionSaluranasliTokyo MX, BS11, Kansai T...

Non expedit (in italiano: non conviene) è una disposizione della Santa Sede con la quale si dichiarò inaccettabile che i cattolici italiani partecipassero alle elezioni politiche del Regno d'Italia e, per estensione, alla vita politica nazionale italiana, sebbene tale divieto non fosse esteso alle elezioni amministrative. La disposizione fu revocata ufficialmente da papa Benedetto XV nel 1919. L'espressione non expedit venne utilizzata per la prima volta dalla Congregazione per gli affari e...

1955 American animated film This article is about the 1955 Walt Disney animated film. For the live-action remake, see Lady and the Tramp (2019 film). For the 2019 film's soundtrack album, see Lady and the Tramp (soundtrack). Lady and the TrampTheatrical release posterDirected by Clyde Geronimi Wilfred Jackson Hamilton Luske Story by Erdman Penner Joe Rinaldi Ralph Wright Don DaGradi Joe Grant Based onHappy Dan, the Cynical Dogby Ward GreeneProduced byWalt DisneyStarring Barbara Luddy Larry Ro...

Questa voce o sezione sull'argomento edizioni di competizioni calcistiche non cita le fonti necessarie o quelle presenti sono insufficienti. Puoi migliorare questa voce aggiungendo citazioni da fonti attendibili secondo le linee guida sull'uso delle fonti. Segui i suggerimenti del progetto di riferimento. Premier League Malti 1981-1982 Competizione Premier League Malti Sport Calcio Edizione 67ª Organizzatore MFA Luogo  Malta Partecipanti 8 Formula 1 girone all'italiana Risultati V...

土库曼斯坦总统土库曼斯坦国徽土库曼斯坦总统旗現任谢尔达尔·别尔德穆哈梅多夫自2022年3月19日官邸阿什哈巴德总统府（Oguzkhan Presidential Palace）機關所在地阿什哈巴德任命者直接选举任期7年，可连选连任首任萨帕尔穆拉特·尼亚佐夫设立1991年10月27日 土库曼斯坦土库曼斯坦政府与政治 国家政府 土库曼斯坦宪法 国旗 国徽 国歌 立法機關（英语：National Council of Turkmenistan） ...

Americans of Belarusian birth or descent Belarusian Americans Беларускія амэрыканцыTotal population600,000[1](without descendants)Regions with significant populationsNew York, New Jersey, Cleveland, Chicago, Los Angeles, DetroitLanguagesBelarusian, Russian, American EnglishReligionPredominantly Orthodoxy, Roman Catholicism, JudaismRelated ethnic groupsRussian Americans, Ukrainian Americans, Rusyn Americans, Polish Americans, other Slavic Americans Part of a series ...

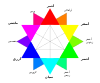
أرجواني   آر جي بي 800080  حول هذه الإحداثيات نظام 16 # ن ش ق (نقبة، إشباع، قيمة) (275°, 92%, 68%) المصدر HTML ب: مضبوط وفق [0–255] (بايت) تعديل مصدري - تعديل   اللون الأرجواني أو الفُرْفير[1] (بالإنجليزية: Purple)‏ هو تسمية تطلق على طيف من تدرجات اللون الواقعة بين الأحمر والأزرق.[2] �...

شداد بن أوس تخطيط اسم الصَّحابي شدَّاد بن أوس ملحوقًا بالترضي عنه - -. معلومات شخصية اسم الولادة شداد بن أوس بن ثابت الميلاد 17 ق.هـالمدينة المنورة الوفاة 58 هـفلسطين[1] الكنية أبو يعلى اللقب الخزرجي الأنصاري الأب أوس بن ثابت أقرباء عمه حسان بن ثابت الحياة العملية الطبقة ص�...

Negative of a convex function In mathematics, a concave function is one for which the value at any convex combination of elements in the domain is greater than or equal to the convex combination of the values at the endpoints. Equivalently, a concave function is any function for which the hypograph is convex. The class of concave functions is in a sense the opposite of the class of convex functions. A concave function is also synonymously called concave downwards, concave down, convex upwards...

For the town in Dumfries and Galloway, see Castle Douglas. Historic siteDouglas CastleDouglas Castle (demolished in 1938)Coordinates55°33′58″N 3°50′10″W / 55.56610°N 3.83624°W / 55.56610; -3.83624 Listed Building – Category C(S)Designated12 January 1971Reference no.LB1449 Location within South Lanarkshire Douglas Castle in 1883 Douglas Castle was a stronghold of the Douglas (later Douglas-Home) family from medieval times to the 20th century. The firs...

Structure des lipopolysaccharides (LPS) Structure d'un lipopolysaccharide (LPS) Les lipopolysaccharides (LPS), également appelés lipoglycanes ou endotoxines, sont de grosses molécules constituées d’un lipide et d’un polysaccharide composé d’un antigène O, d’un noyau externe et d’un noyau interne reliés par une liaison covalente. Ils se trouvent dans la membrane externe des bactéries à Gram négatif. Le lipopolysaccharide (LPS) se lie au récepteur TLR4 et promeut la libéra...

Vowel sound represented by ⟨ʊ⟩ in IPA Near-close near-back rounded vowelʊIPA Number321Audio sample source · helpEncodingEntity (decimal)ʊUnicode (hex)U+028AX-SAMPAUBraille Image IPA: Vowels Front Central Back Close i y ɨ ʉ ɯ u Near-close ɪ ʏ ʊ Close-mid e ø ɘ ɵ ɤ o Mid e̞ ø̞ ə ɤ̞ o̞ Open-mid ɛ œ ɜ ɞ ʌ ɔ Near-open æ ɐ Open a ɶ ä ɑ ɒ IPA help  audio full chart template Legend: unrounded • rounded Spectrogram of ʊ Sa...

American jazz critic and author (born 1948) Giddins speaking at an American Library Association conference in Chicago, 2009. Gary Giddins (born 1948) is an American jazz critic and author.[1] He wrote for The Village Voice from 1973;[1] his Weather Bird column ended in 2003.[2] In 1986, Gary Giddins and John Lewis created the American Jazz Orchestra which presented concerts using a jazz repertory with musicians such as Tony Bennett.[2] For five years, Giddins w...

Palace in Saint Petersburg, Russia 59°56′19″N 30°19′56″E / 59.93861°N 30.33222°E / 59.93861; 30.33222 The Mikhailovsky Palace as it appears today The Mikhailovsky Palace (Russian: Михайловский дворец) is a grand ducal palace in Saint Petersburg, Russia. It is located on Arts Square and is an example of Empire style neoclassicism. The palace currently houses the main building of the Russian Museum and displays its collections of early, folk...

View from Lamb's Rock Catherine Falls seen from Lamb's rock viewpoint Lamb's Rock is a tourist spot in Coonoor, Tamil Nadu, India,[1][2][3] on the slopes of the Nilgiri Hills. It is located at a distance of 8 kilometers from Coonoor. It has a view of the Coimbatore plains,[4] tea estates and coffee estates.[5] References ^ Famous points to see in Coonogj or, a magnificent delight. coonoor.org. Archived from the original on 6 October 2011. Retrieved 15 ...

Роки в кіно   1870-ті   1880-ті 1888 • 1889 1890-ті 1890  • 1891 • 1892 • 1893 • 1894 1895 • 1896 • 1897 • 1898 • 1899 1900-ті 1900 • 1901 • 1902 • 1903 • 1904 1905 • 1906 • 1907 • 1908 • 1909 1910-ті 1910 • 1911 • 1912 • 1913 • 1914 1915 • 1916 • 1917 • 1918 • 1919 1920-ті 1920 • 1...

Логічні сполучники NOT ¬ A , − A , A ¯ , ∼ A {\displaystyle \neg A,-A,{\overline {A}},\sim A} AND A ∧ B , A ⋅ B , A B , A & B , A & & B {\displaystyle A\land B,A\cdot B,AB,A\&B,A\&\&B} OR A ∨ B , A + B , A ∣ B , A ∥ B {\displaystyle A\lor B,A+B,A\mid B,A\parallel B} XOR A ∨ _ B , A ⊕ B {\displaystyle A{\underline {\lor }}B,A\oplus B} еквівалентніс�...

Turkish company Çalık HoldingCompany typePrivateIndustryTextile, energy, construction, finance, and miningFounded1997FounderAhmet ÇalıkHeadquartersŞişli, Istanbul, TurkeyKey peopleAhmet Çalık (chairman)Revenue US$2.8bn[1]Total assets US$8bn[1]Number of employees17,000[1]Websitecalik.com Çalık Holding is a Turkish company that has been operating in the energy, construction, mining, textile, and finance sectors since the 1980s. Founder and chairman Ahmet Çalı...

Disambiguazione – Se stai cercando il gruppo sanguigno A, vedi Sistema AB0. In relazione agli sport automobilistici gestiti dalla FIA, il Gruppo A - definito vetture da turismo di grande produzione[1] - comprende auto che derivano, con una serie di modifiche, dalla produzione di serie.[2] Contrariamente al Gruppo B e al Gruppo C entrambi di breve durata, il Gruppo A fa riferimento ai veicoli derivati dalla produzione di serie limitati in termini di potenza, peso, tecnologia...