Điểm uốn
|
Read other articles:

Duta Besar Indonesia untuk MyanmarLambang Kementerian Luar Negeri Republik IndonesiaPetahanaDicky KomarKuasa Usaha ad interimsejak 31 May 2023KantorYangon, MyanmarDitunjuk olehPresiden IndonesiaPejabat perdanaSuskaDibentukApril 1950[1]Situs webkemlu.go.id/yangon/id Berikut adalah daftar diplomat Indonesia yang pernah menjabat Duta Besar Republik Indonesia untuk Myanmar: No. Foto Nama Mulai menjabat Selesai menjabat Merangkap Diangkat oleh Ref. — MarjunaniPelaksana 1947 1952 ...
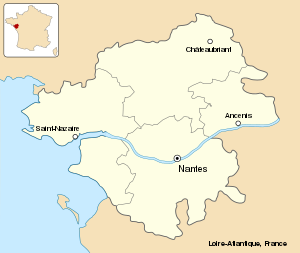
Serangan St NazaireOperasi ChariotBagian dari Kampanye Eropa Barat Laut dalam Perang Dunia IISt Nazaire di LoireTanggal28 Maret 1942LokasiSt Nazaire, Prancis 47°16′30″N 2°11′48″W / 47.27500°N 2.19667°W / 47.27500; -2.19667Koordinat: 47°16′30″N 2°11′48″W / 47.27500°N 2.19667°W / 47.27500; -2.19667Hasil Kemenangan Inggris Semua objektif tercapai Semua target hancurPihak terlibat United Kingdom JermanTokoh dan pe...

AwardVietnam MedalObverse (left), reverse (right)TypeCampaign medalAwarded forCampaign service.DescriptionSilver disk, 36mm diameter.Presented bythemonarch of Australiathemonarch of New ZealandEligibilityAustralian and New Zealand forces.Campaign(s)Vietnam 1964–73.ClaspsNoneEstablished8 June 1968Total18,740 Australian, 3,312 New Zealand.Medal ribbonMedal ribbon with palm for Mentioned in Dispatches Order of WearNext (higher)General Service Medal 1962Next (lower)Vietnam Logistic a...

School district in Texas, United States This article needs additional citations for verification. Please help improve this article by adding citations to reliable sources. Unsourced material may be challenged and removed.Find sources: Mabank Independent School District – news · newspapers · books · scholar · JSTOR (July 2022) (Learn how and when to remove this template message) Introduction to Mabank ISD Mabank Independent School DistrictAddress310 E M...

Cet article est une ébauche concernant le cyclisme. Vous pouvez partager vos connaissances en l’améliorant (comment ?) selon les recommandations des projets correspondants. Championnat des Flandres 2017 GénéralitésCourse102e Championnat des FlandresCompétitionsUCI Europe Tour 2017 1.1Coupe de Belgique de cyclisme sur route 2017Date15 septembre 2017Distance192 kmPays BelgiqueLieu de départKoolskampLieu d'arrivéeKoolskampÉquipes20Partants145Arrivants108Vitesse moyenne44,214 km/...

Синелобый амазон Научная классификация Домен:ЭукариотыЦарство:ЖивотныеПодцарство:ЭуметазоиБез ранга:Двусторонне-симметричныеБез ранга:ВторичноротыеТип:ХордовыеПодтип:ПозвоночныеИнфратип:ЧелюстноротыеНадкласс:ЧетвероногиеКлада:АмниотыКлада:ЗавропсидыКласс:Пт�...

Voce principale: Associazione Sportiva Avellino 1912. AS Avellino 1912Stagione 2012-2013Scenografia della curva Sud del Partenio prima della gara di campionato contro la Nocerina, 25 marzo 2013 Sport calcio Squadra Avellino Allenatore Massimo Rastelli Presidente Walter Taccone Prima Divisione1º posto (promossa in Serie B) Coppa ItaliaSecondo turno Coppa Italia Lega ProSecondo turno Supercoppa di Lega di Prima DivisioneVincitore Maggiori presenzeCampionato: L. Castaldo (28) Miglior marc...

Nicolas WalterBornNicolas Hardy Walter(1934-11-22)22 November 1934South London, EnglandDied7 March 2000(2000-03-07) (aged 65)Milton Keynes, EnglandEducation Rendcomb College Exeter College, Oxford Occupations Writer Journalist Movement Anarchism Anti-war Humanism Spouses Ruth Oppenheim (m. 1962; div. 1982) Christine Morris (m. 1987) Children2, including Natasha WalterParentWilliam Grey Walter (father)Rela...

King of Babylon Marduk-zâkir-šumi IKing of BabylonMarduk-zakir-shumi I, on the Throne Dais of Shalmaneser III at the Iraq MuseumReignc. 855 – 819 BCPredecessorNabû-apla-iddinaSuccessorMarduk-balāssu-iqbiHouseDynasty of E Marduk-zâkir-šumi, inscribed mdAMAR.UTU-za-kir-MU in a reconstruction of two kinglists,[i 1][i 2] 'Marduk pronounced the name',[1] was a king of Babylon from 855 to 819 BC during the mixed dynastic period referred to in antiquity as the dynasty...

Buddhist monastic order in Myanmar Maha Dwara Nikaya (Burmese: မဟာဒွာရနိကာယ, IPA: [məhà dwàɹa̰ nḭkàja̰]); also spelt Maha Dwaya Nikaya or Mahādvāra Nikāya, is a small monastic order of monks in Myanmar (Burma), primarily in Lower Myanmar.[1] This order is very conservative with respect to Vinaya regulations.[2] It is one of 9 legally sanctioned monastic orders (nikaya) in the country, under the 1990 Law Concerning Sangha Organization...
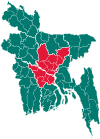
Upazila in Dhaka, BangladeshBaliakandi বালিয়াকান্দিUpazilaCoordinates: 23°38.1′N 89°33′E / 23.6350°N 89.550°E / 23.6350; 89.550Country BangladeshDivisionDhakaDistrictRajbariArea • Total228.99 km2 (88.41 sq mi)Population (2011) • Total207,086 • Density900/km2 (2,300/sq mi)Time zoneUTC+6 (BST)Postal code7730Websitewww.baliakandi.rajbari.gov.bd Baliakandi (Bengali: বা�...

The top basketball league in Switzerland Basketball leagueSB LeagueFounded1931; 93 years ago (1931)First season1931–32CountrySwitzerlandConfederationFIBA EuropeNumber of teams9Level on pyramid1Relegation toLNBDomestic cup(s)Swiss Cup SBL CupInternational cup(s)Champions LeagueFIBA Europe CupCurrent championsFribourg Olympic (20th title) (2022–23)Most championshipsFribourg Olympic (20 titles)WebsiteLink 2023–24 Swiss Basketball League The Swiss Basketball League, also k...

Questa voce sull'argomento militari francesi è solo un abbozzo. Contribuisci a migliorarla secondo le convenzioni di Wikipedia. Segui i suggerimenti del progetto di riferimento. Jean Maximilien LamarqueNascitaSaint-Sever, 22 luglio 1770 MorteParigi, 1° giugno 1832 Dati militariPaese servito Regno di Francia Prima Repubblica francese Primo Impero francese Restaurazione borbonica Monarchia di luglio Forza armata Reale esercito francese Esercito rivoluzionario francese Grand...

Artikel ini memiliki beberapa masalah. Tolong bantu memperbaikinya atau diskusikan masalah-masalah ini di halaman pembicaraannya. (Pelajari bagaimana dan kapan saat yang tepat untuk menghapus templat pesan ini) Artikel ini perlu dirapikan dan ditata ulang agar memenuhi pedoman tata letak Wikipedia. Silakan perbaiki artikel ini agar memenuhi standar Wikipedia. (Pelajari cara dan kapan saatnya untuk menghapus pesan templat ini) Artikel ini membutuhkan rujukan tambahan agar kualitasnya dapat dip...

Painting by Jacques-Louis David Saint Jerome Hears the Trumpet of the Last Judgmentfr: Saint Jérôme entendant la trompette du Jugement dernierArtistJacques-Louis DavidYear1779 (1779)SubjectJeromeLocationMontreal Museum of Fine Arts on loan from the Musée de la civilisation[1]OwnerNotre‑Dame‑de‑Québec Parish Corporation[1] Saint Jerome Hears the Trumpet of the Last Judgment is a 1779 painting by the French artist Jacques-Louis David. Description Jerome, one of th...

English bank Former head office of Parr's Bank, 214 High Holborn in London Parr's Bank Limited was a bank that existed from 1782 to 1918. It was founded as Parr & Co. in Warrington, then in the county of Lancashire in the United Kingdom. In 1918 it was acquired by London County and Westminster Bank, and it was thus one of the predecessors of NatWest Group. History Former Warrington main branch of Parr's Bank Liverpool City Office, formerly Parr's Bank, designed by Richard Norman Shaw in 1...

French runner Gabriel TualGabriel Tual, 2022Personal informationBorn (1998-04-09) 9 April 1998 (age 26)Villeneuve-sur-Lot, FranceSportSportAthleticsEvent800 metresClubUs Talence Medal record Men's athletics Representing France Event 1st 2nd 3rd European Championships 1 0 0 Total 1 0 0 European Championships 2024 Rome 800 m Gabriel Tual (born 9 April 1998) is a French middle-distance runner specialising in the 800 metres.[1] His personal best time is 1:44.28, which he r...

Peta infrastruktur dan tata guna lahan di Komune Blennes. = Kawasan perkotaan = Lahan subur = Padang rumput = Lahan pertanaman campuran = Hutan = Vegetasi perdu = Lahan basah = Anak sungaiBlennesNegaraPrancisArondisemenFontainebleauKantonLorrez-le-Bocage-PréauxAntarkomunetidak ada pada 2007Pemerintahan • Wali kota (2008-2014) François Canterini • Populasi1477Kode INSEE/pos77035 / 2 Population sans doubles comptes: ...

Cet article est une ébauche concernant un musicien britannique et le jazz. Vous pouvez partager vos connaissances en l’améliorant (comment ?) selon les recommandations des projets correspondants. Pour les articles homonymes, voir Hayes. Tubby Hayes Données clés Nom de naissance Edward Brian Hayes Naissance 30 janvier 1935St Pancras, Londres, Angleterre Décès 8 juin 1973 (à 38 ans)Hammersmith, Londres, Angleterre Genre musical Jazz Instruments Saxophone ténor, vibraphone, ...

Memoriale agli omosessuali, sia uomini che donne, vittime del nazionalsocialismo a Colonia in Germania. L'iscrizione su uno dei due lati del monumento recita: Totgeschlagen – Totgeschwiegen (Colpito a morte - Messo a tacere) Questa voce o sezione sugli argomenti LGBT e nazismo è priva o carente di note e riferimenti bibliografici puntuali. Sebbene vi siano una bibliografia e/o dei collegamenti esterni, manca la contestualizzazione delle fonti con note a piè di pagina o altri riferime...





















