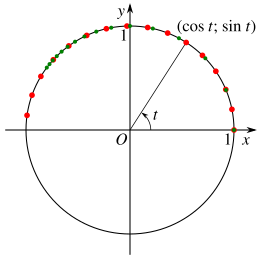
Phương trình tham số
|
Read other articles:

Lars EidingerEidinger pada 2014Lahir21 Januari 1976 (umur 48)Berlin, JermanPekerjaanPemeranTahun aktif2002—kiniSuami/istriUlrike EidingerAnak1 Lars Eidinger (Jerman: [laʁs ˈaɪ̯dɪŋɐ] ⓘ; lahir 21 Januari 1976) adalah seorang pemeran asal Jerman. Eidinger memulai karirnya di Teater Deutsches pada 1997. Filmografi pilihan 2005: See You at Regis Debray 2009: Everyone Else 2011: Hell 2012: Goltzius and the Pelican Company 2012: Home for the Weekend 2013: Foyle’s War ...

Mihir Bose Mihir Bose (lahir 12 Januari 1947)[1] adalah seorang jurnalis dan penulis India Britania. Ia menulis sebuah mingguan Big Sports Interview untuk London Evening Standard, dan juga menulis dan menyiarkan tentang masalah olahraga dan sosial dan sejarah untuk beberapa outlet termasuk BBC, Financial Times dan Sunday Times. Ia adalah BBC Sports Editor hingga 4 Agustus 2009.[2] Bose dikabarkan tidak senang dengan rencana kepindahan Departemen BBC Sports dari London ke Manch...

Artikel atau sebagian dari artikel ini mungkin diterjemahkan dari List of Sultans of Zanzibar di en.wikipedia.org. Isinya masih belum akurat, karena bagian yang diterjemahkan masih perlu diperhalus dan disempurnakan. Jika Anda menguasai bahasa aslinya, harap pertimbangkan untuk menelusuri referensinya dan menyempurnakan terjemahan ini. Anda juga dapat ikut bergotong royong pada ProyekWiki Perbaikan Terjemahan. (Pesan ini dapat dihapus jika terjemahan dirasa sudah cukup tepat. Lihat pula: pand...

Pacific severe tropical storm in 2022 This article is about the 2022 tropical storm. For other storms of the same name, see List of storms named Nalgae and List of storms named Paeng. Severe Tropical Storm Nalgae (Paeng) Nalgae at peak intensity on November 1Meteorological historyFormedOctober 26, 2022DissipatedNovember 3, 2022Severe tropical storm10-minute sustained (JMA)Highest winds110 km/h (70 mph)Lowest pressure975 hPa (mbar); 28.79 inHgCategory 1-equivalent typh...

Bukan Malin KundangSutradaraIqbal RaisProduserGope T. SamtaniSubagio S.Ditulis olehHilman MutasiSemaliPemeranRinggo Agus RahmanDeddy Mahendra DestaSissy PriscilliaAmingJaja MihardjaJoe P ProjectPerusahaanproduksiRapi FilmsDistributorRapi FilmsTanggal rilis23 Desember 2009Durasi90 menitNegaraIndonesia Bukan Malin Kundang adalah film Indonesia dari Rapi Film yang dirilis 23 Desember 2009 dengan disutradarai oleh Iqbal Rais dan dibintangi oleh Ringgo Agus Rahman, Deddy Mahendra Desta, Sissy Pris...

Chemical elements in groups 1, 2, 13–18 The periodic table of the chemical elements. The columns represent the groups. Groups 1, 2 and 13 to 18 constitute the main group. Sometimes groups 3 and 12, as well as the lanthanides and actinides (the two rows at the bottom), are also included in the main group. In chemistry and atomic physics, the main group is the group of elements (sometimes called the representative elements) whose lightest members are represented by helium, lithium, beryllium,...

Strada statale 45 bisGardesana OccidentaleLocalizzazioneStato Italia Regioni Lombardia Trentino-Alto Adige Province Cremona Brescia Trento DatiClassificazioneStrada statale InizioCremona FineTrento Lunghezza154,160 km Provvedimento di istituzioneR.D. 22 luglio 1932, n. 1046 GestoreTratte ANAS: da Cremona fino al confine con la Provincia autonoma di Trento; dal 1998 la gestione del tratto dal confine con la Lombardia a Riva del Garda a Trento è passata alla Provi...

فيشال بهاردساج معلومات شخصية الميلاد 4 أغسطس 1965 (59 سنة)[1] مواطنة الهند الحياة العملية المهنة مخرج أفلام، ومغني، وملحن، وكاتب سيناريو، وشاعر غنائي، وكاتب أغاني، ومخرج موسيقي [لغات أخرى]، ومنتج أفلام المواقع IMDB صفحته على IMDB&#...

Untuk satuan berat, lihat pound (berat).Pound sterlingPound sterling (Inggris)Berkas:2016 £1 coin.jpgUang koin poundISO 4217KodeGBPNomor826Eksponen2DenominasiSubsatuan 1/100pennyBentuk jamakpounds pennypenceSimbol£ pennypJulukanQuid (tunggal dan jamak)Uang kertas Sering digunakan£5, £10, £20, £50 Jarang digunakan£1, £100Uang koin1p, 2p, 5p, 10p, 20p, 50p, £1, £2DemografiPengguna Britania Raya 9 teritori Britania Teritori Antarktika Britania &...

Amerika SerikatJulukanYanks, The Stars & Stripes (Bintang & Garis)[1]The Red, White and Blue (Merah, Putih dan Biru)[2]AsosiasiFederasi Sepak Bola Amerika Serikat (USSF)KonfederasiCONCACAF (Amerika Utara, Tengah, dan Karibia)Sub-konfederasiNAFU (Amerika Utara)Pelatih Gregg Berhalter[3]KaptenChristian PulisicPenampilan terbanyakCobi Jones (164)Pencetak gol terbanyakLandon Donovan & Clint Dempsey (57)Stadion kandangBervariasi (sesuai kebutuhan)Peringkat FIFAT...

1960 South African republic referendum 5 October 1960 Are you in favour of a Republic for the Union?Results Choice Votes % Yes 850,458 52.29% No 775,878 47.71% Valid votes 1,626,336 99.52% Invalid or blank votes 7,904 0.48% Total votes 1,634,240 100.00% Registered voters/turnout 1,800,426 90.77% Results by provinceFront page of Die Transvaler, 7 October 1960, announcing republican victory by 70,000 votes A referendum on becoming a republic was held in South Africa on 5 October 1960. The Afri...

WorkSingel oleh Rihanna featuring Drakedari album AntiBahasaBajan CreolePatwa JamaikaInggrisDirilis27 Januari 2016 (2016-01-27)DirekamDesember 2015GenreDancehallreggae-popR&BDurasi3:39LabelRoc NationWestbury RoadPenciptaJahron BrathwaiteMatthew SamuelsAllen RitterRupert Thomas Jr.Aubrey GrahamRobyn FentyMonte MoirProduserBoi-1daKronologi singel Rihanna American Oxygen (2015) Work (2016) Kiss It Better / Needed Me(2016) Kronologi singel Drake Jumpman(2015) Work(2016) Summer ...

FCF1 المعرفات الأسماء المستعارة FCF1, Bka, C14orf111, UTP24, CGI-35, rRNA-processing protein, rRNA-processing protein معرفات خارجية MGI: MGI:1920986 HomoloGene: 5706 GeneCards: 51077 علم الوجود الجيني الوظيفة الجزيئية • RNA binding المكونات الخلوية • small-subunit processome• نوية• نواة• بلازم نووي العمليات الحيوية • نشأة الريبوسوم• rRNA processing• en...

Space exploration using nuclear energy The KIWI A prime nuclear thermal rocket engine Mars Curiosity rover powered by a RTG on Mars. White RTG with fins is visible at far side of rover. Nuclear power in space is the use of nuclear power in outer space, typically either small fission systems or radioactive decay for electricity or heat. Another use is for scientific observation, as in a Mössbauer spectrometer. The most common type is a radioisotope thermoelectric generator, which has been use...

Voce principale: Offenbacher Fußball-Club Kickers 1901. Offenbacher Fußball-Club Kickers 1901Stagione 1994-1995Sport calcio Squadra Kickers Offenbach Allenatore Wilfried Kohls All. in seconda Stephan Groß Regionalliga sud15° posto Coppa di GermaniaSecondo turno 1993-1994 1995-1996 Si invita a seguire il modello di voce Questa voce raccoglie le informazioni riguardanti l'Offenbacher Fußball-Club Kickers 1901 nelle competizioni ufficiali della stagione 1994-1995. Indice 1 Stagione 2 ...

此條目可参照英語維基百科相應條目来扩充。 (2021年5月6日)若您熟悉来源语言和主题,请协助参考外语维基百科扩充条目。请勿直接提交机械翻译,也不要翻译不可靠、低品质内容。依版权协议,译文需在编辑摘要注明来源,或于讨论页顶部标记{{Translated page}}标签。 约翰斯顿环礁Kalama Atoll 美國本土外小島嶼 Johnston Atoll 旗幟颂歌:《星條旗》The Star-Spangled Banner約翰斯頓環礁�...

本條目存在以下問題,請協助改善本條目或在討論頁針對議題發表看法。 此條目的引用需要清理,使其符合格式。参考文献应符合正确的引用、脚注及外部链接格式。 此條目可参照英語維基百科相應條目来扩充,此條目在對應語言版為高品質條目。 (2023年8月17日)若您熟悉来源语言和主题,请协助参考外语维基百科扩充条目。请勿直接提交机械翻译,也不要翻译不可靠、低�...

Cricket team For the men's team, see Norway national cricket team. NorwayFlag of NorwayAssociationNorwegian Cricket BoardInternational Cricket CouncilICC statusAssociate member[1] (2017) Affiliate member (2000)ICC regionEuropeICC Rankings Current[3] Best-everWT20I 61st 50th (23 Dec 2022) [2]Women's Twenty20 InternationalsFirst WT20Iv. Austria at Parc du Grand Blottereau, Nantes; 31 July 2019Last WT20Iv. Sweden at Tikkurila Cricket Ground, Vantaa; 27 Au...

Major daily newspaper published in Salem, Oregon, United States Statesman JournalThe July 27, 2005, front page of theStatesman JournalTypeDaily newspaperFormatBroadsheetOwner(s)GannettPublisherRyan Kedzierski[1]EditorCherrill Crosby[1]Founded1851(as Oregon Statesman)Headquarters340 Vista Ave. SESalem, OR 97301USACirculation27,859 Mon-Tue, Thur33,815 Wed.36,323 Sun[2]ISSN0739-5507Websitestatesmanjournal.com The Statesman Journal is the major daily newspaper published i...

Sybra sulcata Klasifikasi ilmiah Kerajaan: Animalia Filum: Arthropoda Kelas: Insecta Ordo: Coleoptera Famili: Cerambycidae Subfamili: Lamiinae Tribus: Apomecynini Genus: Sybra Spesies: Sybra sulcata Sybra sulcata adalah spesies kumbang tanduk panjang yang berasal dari famili Cerambycidae. Spesies ini juga merupakan bagian dari genus Sybra, ordo Coleoptera, kelas Insecta, filum Arthropoda, dan kingdom Animalia. Larva kumbang ini biasanya mengebor ke dalam kayu dan dapat menyebabkan kerusakan ...