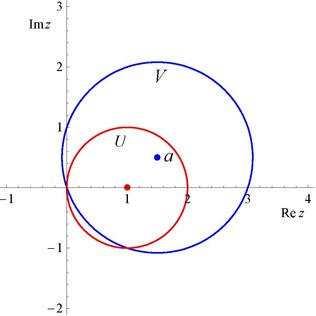
Thác triển giải tích
|
Read other articles:

Sejarah Māori bermula dengan kedatangan penduduk Polinesia di Selandia Baru (Aotearoa dalam bahasa Māori). Migrasi lintas-samudera ini dilakukan menggunakan kano di antara akhir abad ke-13 hingga awal abad ke-14. Setelah beberapa abad terisolasi, pemukim Polinesia ini kemudian membentuk budaya mereka sendiri. Mereka kemudian dikenal sebagai suku Māori. Sejarah awal Māori umumnya dibagi menjadi dua periode: periode Arkais (sekitar 1300-1500) dan periode Klasik (sekitar 1500-1642). Situs ar...

Artikel ini sebatang kara, artinya tidak ada artikel lain yang memiliki pranala balik ke halaman ini.Bantulah menambah pranala ke artikel ini dari artikel yang berhubungan atau coba peralatan pencari pranala.Tag ini diberikan pada Januari 2023. Javier Arizmendi Informasi pribadiNama lengkap Ángel Javier Arizmendi de LucasTanggal lahir 3 Maret 1984 (umur 40)Tempat lahir Madrid, SpanyolTinggi 1,90 m (6 ft 3 in)Posisi bermain Penyerang, sayapKarier junior Atlético MadridKar...

Darul Uloom Deoband (est. 1866) Daftar pustaka karya Darul Uloom Deoband ini adalah daftar pilihan sumber ilmiah yang tersedia secara umum terkait dengan Darul Uloom Deoband, sebuah seminari Islam terkemuka dan pusat teologi Muslim di India tempat gerakan Deobandi dimulai, didirikan pada tahun 1866.[1][2] Ini adalah salah satu gerakan reformasi paling berpengaruh dalam Islam modern. Ini membanggakan jaringan madrasah satelit terbesar di seluruh dunia terutama India, Bangladesh...

Seorang jaksa pribumi di Hindia Belanda pada tahun 1870-an. Jaksa (Sanskerta: adhyakṣa; Inggris: prosecutor; bahasa Belanda: officier van justitie) adalah pegawai pemerintah dalam bidang hukum yang bertugas menyampaikan dakwaan atau tuduhan di dalam proses pengadilan terhadap orang yang diduga telah melanggar hukum. Berdasarkan Undang-Undang Republik Indonesia Nomor 16 Tahun 2004 tentang Kejaksaan Republik Indonesia yang dimaksud dengan Jaksa adalah Pejabat Fungsional yang diberi wewenang o...

Town in Arizona Town in Arizona, United StatesParker, ArizonaTownHistoric Downtown Parker FlagLocation of Parker in La Paz County, ArizonaParker, ArizonaLocation in the United StatesCoordinates: 34°8′41″N 114°17′23″W / 34.14472°N 114.28972°W / 34.14472; -114.28972[1]CountryUnited StatesStateArizonaCountyLa PazNamed forEly S. ParkerGovernment • MayorKaren Bonds • Vice MayorJerry Hooper • Town CouncilRandy Hartless ...

Dennis Kucinich Dennis John Kucinich (/kuːˈsɪnɪtʃ/; lahir 8 Oktober 1946) adalah seorang politikus Amerika Serikat. Sebagai anggota DPR Amerika Serikat dari Ohio, yang menjabat dari 1997 sampai 2013, ia juga menjadi kandidat untuk nominasi Partai Demokrat untuk jabatan presiden Amerika Serikat pada 2004 sampai 2008. Pranala luar Cari tahu mengenai Dennis Kucinich pada proyek-proyek Wikimedia lainnya: Gambar dan media dari Commons Berita dari Wikinews Kutipan dari Wikiquote Teks sumber da...

PT Mega Asset ManagementJenisJasa keuangan/publikDidirikan2011Kantorpusat Jakarta, IndonesiaPemilikMega CorporaSitus webwww.mega-asset.co.id Mega Asset Management atau yang lebih dikenal sebagai Mega Asset adalah salah satu perusahaan manajemen investasi yang berdiri sejak 2011, dan berkantor pusat di Jakarta dan mempunyai cabang di berbagai kota besar di Indonesia. Perusahaan ini berada dibawah kepemilikan CT Corp melalui Mega Corpora. Reksa Dana Mega Asset telah menerima sejumlah penghargaa...

Voce principale: Associazione Sportiva Dilettantistica Fidelis Andria 1928. Associazione Sportiva Fidelis AndriaStagione 2000-2001Sport calcio Squadra Fidelis Andria Allenatore Leonardo Bitetto poi Stefano Boggia poi Hector Alberto Ortega poi Leonardo Bitetto Presidente Giuseppe Fuzio Serie C115º posto nel girone B. Maggiori presenzeCampionato: Sgarra (30) Miglior marcatoreCampionato: Biancolino, Capparella (4) 1999-2000 2001-2002 Si invita a seguire il modello di voce Questa pagina ra...

この項目には、一部のコンピュータや閲覧ソフトで表示できない文字が含まれています(詳細)。 数字の大字(だいじ)は、漢数字の一種。通常用いる単純な字形の漢数字(小字)の代わりに同じ音の別の漢字を用いるものである。 概要 壱万円日本銀行券(「壱」が大字) 弐千円日本銀行券(「弐」が大字) 漢数字には「一」「二」「三」と続く小字と、「壱」「�...

US music distributor Not to be confused with Red Records. For the Australian music channel, see Channel V Australia. For the Vietnamese genre of communist music sometimes referred to as Red music, see Nhạc đỏ. This article has multiple issues. Please help improve it or discuss these issues on the talk page. (Learn how and when to remove these template messages) A major contributor to this article appears to have a close connection with its subject. It may require cleanup to comply with W...

Ця стаття потребує додаткових посилань на джерела для поліпшення її перевірності. Будь ласка, допоможіть удосконалити цю статтю, додавши посилання на надійні (авторитетні) джерела. Зверніться на сторінку обговорення за поясненнями та допоможіть виправити недоліки. Мат...

Kartini School di Batavia (Jakarta) Opening of the Katrini School di Buitzenborg (Bogor) Mei 1915 Bangunan Kartini School di Buitenzorg (dibuka 1918) Ruang kelas Kartini school di Malang Kartini School atau Sekolah Kartini adalah sekolah khusus untuk perempuan yang didirikan oleh Yayasan van Deventer di beberapa tempat untuk mendidikan para siswa perempuan berdasarkan keinginan Raden Ajeng Kartini. Awalnya berdiri tahun 1912 di Semarang. Latar Belakang Kartini School Pada masa keuasaan VOC ak...

本條目存在以下問題,請協助改善本條目或在討論頁針對議題發表看法。 此條目需要編修,以確保文法、用詞、语气、格式、標點等使用恰当。 (2013年8月6日)請按照校對指引,幫助编辑這個條目。(幫助、討論) 此條目剧情、虛構用語或人物介紹过长过细,需清理无关故事主轴的细节、用語和角色介紹。 (2020年10月6日)劇情、用語和人物介紹都只是用於了解故事主軸,輔助�...
Japanese rugby union club, based in Nagoya Toyota Jido Shokki redirects here. For the company, see Toyota Industries. Rugby teamToyota Industries Shuttles Aichi 豊田自動織機シャトルズ愛知UnionJapan Rugby Football UnionNickname(s)ShuttlesFounded1984; 40 years ago (1984)LocationKariya, AichiGround(s)Mizuho Rugby Stadium (Capacity: 15,000)ChairmanTakuo SasakiCoach(es)Yoichi TokunoLeague(s)Japan Rugby League One, Division Two20221st Promoted to Division Two Team kit...

فرديناند ماركوس (بالإنجليزية: Ferdinand Emmanuel Edralin Marcos)، و(بالتاغالوغية: Ferdinand Emmanuel Edralin Marcos)، و(بالإسبانية: Ferdinand Emmanuel Edralin Marcos)، و(بالإيلوكانوية: Ferdinand Emmanuel Edralin Marcos) مناصب عضو مجلس النواب في الفلبين عضو خلال الفترة30 ديسمبر 1949 – 30 ديسمبر 1959 فترة برلمانية كون...

City in Wisconsin, United StatesWest Allis, WisconsinCityWest Allis Historical MuseumLocation of West Allis in Milwaukee County, Wisconsin.Coordinates: 43°0′29″N 88°1′6″W / 43.00806°N 88.01833°W / 43.00806; -88.01833Country United StatesStateWisconsinCountyMilwaukeeGovernment • TypeMayor-Council • MayorDan DevineArea[1] • Total11.40 sq mi (29.54 km2) • Land11.38 sq mi (29...
City in Lorestan province, Iran For the village in Selseleh County, see Momenabad. For the village in Qom province, see Momenabad. For the administrative division of South Khorasan province, see Momenabad Rural District. For other places with the same name, see Mowmenabad. City in Lorestan, IranMomenabad Persian: مؤمنآبادCityMomenabadCoordinates: 33°35′35″N 49°31′26″E / 33.59306°N 49.52389°E / 33.59306; 49.52389[1]CountryIranProvinceLores...

Method of running software Computerized batch processing is a method of running software programs called jobs in batches automatically. While users are required to submit the jobs, no other interaction by the user is required to process the batch. Batches may automatically be run at scheduled times as well as being run contingent on the availability of computer resources. History The term batch processing originates in the traditional classification of methods of production as job production ...

小半森林公園の大水車 小半鍾乳洞(おながらしょうにゅうどう)は、大分県佐伯市本匠(旧本匠村)小半にある鍾乳洞。1922年(大正11年)3月8日に大分県で初めて国の天然記念物に指定されている。 概要 小半鍾乳洞大分市 小半鍾乳洞の位置 この鍾乳洞は、1899年(明治32年)に発見されたもので、清流として知られる番匠川の源流の近くにある。全長1,750mで、そのうち3...

Class of Japanese battleships Kawachi at anchor Class overview NameKawachi class Builders Yokosuka Naval Arsenal Kure Naval Arsenal Operators Imperial Japanese Navy Preceded bySatsuma class Succeeded byFusō class Built1909–1912 In service1912–1945 In commission1912–1923 Completed2 Lost1 Scrapped1 General characteristics TypeDreadnought battleship Displacement20,823–21,443 long tons (21,157–21,787 t) (normal) Length526–533 ft (160.3–162.5 m) Beam84 ...