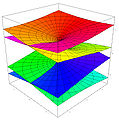
Mặt Riemann
|
Read other articles:

Artikel ini perlu diwikifikasi agar memenuhi standar kualitas Wikipedia. Anda dapat memberikan bantuan berupa penambahan pranala dalam, atau dengan merapikan tata letak dari artikel ini. Untuk keterangan lebih lanjut, klik [tampil] di bagian kanan. Mengganti markah HTML dengan markah wiki bila dimungkinkan. Tambahkan pranala wiki. Bila dirasa perlu, buatlah pautan ke artikel wiki lainnya dengan cara menambahkan [[ dan ]] pada kata yang bersangkutan (lihat WP:LINK untuk keterangan lebih lanjut...

ZimniceaKota Lambang kebesaranNegara RumaniaProvinsiTeleormanStatusKotaPemerintahan • Wali kotaPetre Pîrvu (Partidul Social Democrat)Luas • Total131,31 km2 (5,070 sq mi)Populasi (2002) • Total16.500Zona waktuUTC+2 (EET) • Musim panas (DST)UTC+3 (EEST) Zimnicea adalah kota yang terletak di provinsi Teleorman, Rumania. Kota ini merupakan kota pelabuhan di tepi sungai Donau yang berseberangan dengan kota Svishtov di Bulgar...

У этого термина существуют и другие значения, см. Якиманка. Большая Якиманка Общая информация Страна Россия Город Москва Округ ЦАО Район Якиманка Протяжённость 1,3 км Метро 05 Октябрьская06 Октябрьская 09 Полянка01 Кропоткинская Медиафайлы на Викискладе Больша́я Якима́н...

Об экономическом термине см. Первородный грех (экономика). ХристианствоБиблия Ветхий Завет Новый Завет Евангелие Десять заповедей Нагорная проповедь Апокрифы Бог, Троица Бог Отец Иисус Христос Святой Дух История христианства Апостолы Хронология христианства Ран�...

Part of a series onEthnicity in Washington, D.C. African Americans Ethiopians Hispanics Irish Jews Koreans Native Americans vte Maple School of Irish Dance at the 48th Annual St. Patrick’s Day Parade of Washington, DC (2018) People of Irish descent form a distinct ethnic group in Washington, D.C.,[1] and have had a presence in the region since the pre-American Revolution period.[2] History 18th century By the mid to late 1700s, there were a number of first- and second-gener...

This article uses bare URLs, which are uninformative and vulnerable to link rot. Please consider converting them to full citations to ensure the article remains verifiable and maintains a consistent citation style. Several templates and tools are available to assist in formatting, such as reFill (documentation) and Citation bot (documentation). (August 2022) (Learn how and when to remove this template message) This article includes a list of general references, but it lacks sufficient corresp...

Mimicry of a less deadly species The deadly Texas coral snake, Micrurus tener (the Emsleyan/Mertensian mimic) The harmless Mexican milk snake, Lampropeltis triangulum annulata (the Batesian mimic) Emsleyan mimicry, also called Mertensian mimicry, describes an unusual type of mimicry where a deadly prey mimics a less dangerous species.[1] History Emsleyan mimicry was first proposed by M. G. Emsley[2] as a possible explanation for how a predator species could learn to avoid an a...

1968 song by the BeatlesThe Continuing Story of Bungalow BillCover of the song's sheet musicSong by the Beatlesfrom the album The Beatles Released22 November 1968Recorded8 October 1968StudioEMI, LondonGenreFolk rockLength3:18LabelAppleSongwriter(s)Lennon–McCartneyProducer(s)George Martin The Continuing Story of Bungalow Bill is a song written by John Lennon (credited to Lennon–McCartney), and released by the English rock band the Beatles on their 1968 double album The Beatles (also known...

Ne doit pas être confondu avec Belle et Sébastien. Pour les articles homonymes, voir B&S. Belle and Sebastian De gauche à droite : Mick Cooke, Richard Colburn, Bobby Kildea, Chris Geddes, Stevie Jackson, Sarah Martin, et Stuart Murdoch.Informations générales Pays d'origine Royaume-Uni Genre musical Indie pop[1], folk rock[2],[1], pop de chambre[3],[4] Années actives Depuis 1996 Labels Rough Trade, Jeepster Records, Matador Records, Arts and Crafts México, Sanctuary Site offic...

2005 Canadian filmWhy We FightTheatrical posterDirected byEugene JareckiWritten byEugene JareckiProduced bySusannah ShipmanStarringJoseph CirincioneRichard PerleChalmers JohnsonJohn McCainCinematographyEtienne SauretMay Ying WelshEdited byNancy KennedyMusic byRobert MillerProductioncompaniesARTEBBC StoryvilleCBCCharlotte Street FilmsTV2 DanmarkDistributed bySony Pictures Classics (US)Axiom Films (UK & Ireland)Release dates January 2005 (2005-01) (Sundance) January 22,&...

Topik artikel ini mungkin tidak memenuhi kriteria kelayakan Wikipedia:Kelayakan artikel/Akademik. Harap penuhi kelayakan artikel dengan: menyertakan sumber-sumber tepercaya yang independen terhadap subjek dan sebaiknya hindari sumber-sumber trivial. Jika tidak dipenuhi, artikel ini harus digabungkan, dialihkan ke cakupan yang lebih luas, atau dihapus oleh Pengurus.Cari sumber: SD Ukhuwwatul Islamiyah – berita · surat kabar · buku · cendekiawan · JSTOR ...

Nickelodeon on Sunset con la ambientación de Victorious en mayo de 2011 Nickelodeon on Sunset (también llamado Nick on Sunset) anteriormente conocido como Earl Carroll Theatre, fue una instalación de escenario ubicado en 6230 Sunset Boulevard, en Hollywood, California, construido por el showman Eric Carroll y diseñado en el estilo Streamline moderne por el arquitecto Gordon Kaufmann en 1938. El teatro ha sido conocido por varios nombres desde entonces, incluido el Moulin Rouge de 1953 a 1...

Feature of viruses This article needs additional citations for verification. Please help improve this article by adding citations to reliable sources. Unsourced material may be challenged and removed.Find sources: Viral tegument – news · newspapers · books · scholar · JSTOR (May 2009) (Learn how and when to remove this message) Location of the viral tegument A viral tegument or tegument, more commonly known as a viral matrix, is a cluster of proteins t...

Concept of social inter-connectedness of all people For other uses, see Six degrees (disambiguation). Not to be confused with Six degrees of freedom. A map of several branches and degrees of a small social group: Ryan is six degrees of separation from Pablo Six degrees of separation is the idea that all people are six or fewer social connections away from each other. As a result, a chain of friend of a friend statements can be made to connect any two people in a maximum of six steps. It is al...

Artikel ini membutuhkan rujukan tambahan agar kualitasnya dapat dipastikan. Mohon bantu kami mengembangkan artikel ini dengan cara menambahkan rujukan ke sumber tepercaya. Pernyataan tak bersumber bisa saja dipertentangkan dan dihapus.Cari sumber: Madrasah – berita · surat kabar · buku · cendekiawan · JSTOR Bagian dari seri bertopik IslamUshul fikih Sumber-sumber hukum Islam Al-Qur'an Hadis Ijmak Qiyas Istihsan Ijtihad Urf Fikih Taqlid Mazhab Bidah Mad...

13th-century crusade A knight of the Psitticher faction of Basel, from the Codex Manesse (early 14th century). Both of the leaders of the Crusade of 1267 were Psittichers. vteCrusadesIdeology and institutions Crusading movement In the Holy Land (1095–1291) First 1101 Norwegian Venetian 1129 Second Third 1197 Fourth Fifth Sixth Barons' Seventh 1267 Catalan Eighth Lord Edward's Fall of Outremer Later Crusades (1291–1717) Crusades after Acre, 1291–1399 Aragonese Smyrniote Alexandri...
Cet article est une ébauche concernant le ski et la Finlande. Vous pouvez partager vos connaissances en l’améliorant (comment ?) selon les recommandations des projets correspondants. Championnats du mondede ski nordique 2017 Généralités Sport Ski nordique Organisateur(s) FIS Édition 51e Lieu(x) Lahti, Finlande Date 22 février au 5 mars 2017 Site web officiel lahti2017.fi Navigation Falun 2015 Seefeld 2019 modifier Les championnats du monde de ski nordique 2017 sont la 51e édit...

Part of a series onRhetoric History Ancient Greece Asianism Atticism Attic orators Calliope Sophists Ancient India Ancient Rome The age of Cicero Second Sophistic Middle Ages Byzantine rhetoric Trivium Renaissance Studia humanitatis Modern period Concepts Captatio benevolentiae Chironomia Decorum Delectare Docere Device Eloquence Eloquentia perfecta Eunoia Enthymeme Facilitas Fallacy Informal Figure of speech Scheme Trope Five canons Inventio Dispositio Elocutio Memoria Pronuntiatio Hypsos Im...

American baseball player (born 1965) Baseball player Larry CasianCasian with the Orlando Twins c. 1988PitcherBorn: (1965-10-28) October 28, 1965 (age 58)Lynwood, California, U.S.Batted: RightThrew: LeftMLB debutSeptember 9, 1990, for the Minnesota TwinsLast MLB appearanceMay 18, 1998, for the Chicago White SoxMLB statisticsWin–loss record11–13Earned run average4.56Strikeouts125 Teams Minnesota Twins (1990–1994) Cleveland Indians (1994) Chicago Cubs (19...

Indian Bengali-language writer This article needs additional citations for verification. Please help improve this article by adding citations to reliable sources. Unsourced material may be challenged and removed.Find sources: Achintya Kumar Sengupta – news · newspapers · books · scholar · JSTOR (January 2019) (Learn how and when to remove this message) Achintya Kumar SenguptaBorn(1903-09-19)19 September 1903Noakhali, Bengal Presidency, British IndiaDie...