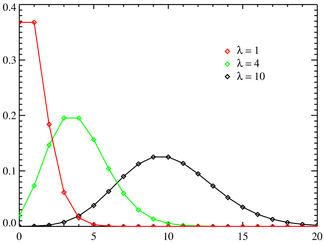
Phأ¢n phل»‘i Poisson
| |||||||||||||||||||||||||||||||
Read other articles:

Questa voce o sezione sull'argomento filosofia non cita le fonti necessarie o quelle presenti sono insufficienti. Puoi migliorare questa voce aggiungendo citazioni da fonti attendibili secondo le linee guida sull'uso delle fonti. Segui i suggerimenti del progetto di riferimento. PoeticaTitolo originaleخ خµدپل½¶ د€خ؟خ¹خ·د„خ¹خ؛ل؟†د‚ Prima pagina della Poetica nell'edizione di Bekker (1837) AutoreAristotele 1آھ ed. originaleIV secolo a.C. Generetrattato Lingua originalegreco antico Modific...

Si ce bandeau n'est plus pertinent, retirez-le. Cliquez ici pour en savoir plus. Cet article ne cite pas suffisamment ses sources (juin 2018). Si vous disposez d'ouvrages ou d'articles de rأ©fأ©rence ou si vous connaissez des sites web de qualitأ© traitant du thأ¨me abordأ© ici, merci de complأ©ter l'article en donnant les rأ©fأ©rences utiles أ sa vأ©rifiabilitأ© et en les liant أ la section آ« Notes et rأ©fأ©rences آ». En pratique : Quelles sources sont attendues ? Comm...

Mimpiku Jadi NyataKompilasi karya 5 besar finalis Indonesian Idol Junior musim ketigaDirilis22 November 2019Direkam2019GenrePopDurasi46:25LabelRANS MusicMega MusicProduser Raffi Ahmad Nagita Slavina Mimpiku Jadi Nyata adalah sebuah album yang diproduksi oleh RANS Music bekerja sama dengan Mega Music dan menjadi jalur lagu orisinal dari seri web Mimpiku Jadi Nyata. Sebelumnya dirilis dalam bentuk digital, album ini kemudian diluncurkan dalam bentuk CD. Untuk distribusi CD, RANS Music mengg...

Si ce bandeau n'est plus pertinent, retirez-le. Cliquez ici pour en savoir plus. Cet article ne cite pas suffisamment ses sources (aoأ»t 2018). Si vous disposez d'ouvrages ou d'articles de rأ©fأ©rence ou si vous connaissez des sites web de qualitأ© traitant du thأ¨me abordأ© ici, merci de complأ©ter l'article en donnant les rأ©fأ©rences utiles أ sa vأ©rifiabilitأ© et en les liant أ la section آ« Notes et rأ©fأ©rences آ». En pratique : Quelles sources sont attendues ? Com...

Disambiguazione – Se stai cercando l'omonima designazione societaria della AC Salernitana Femminile, attiva dal 1982 al 2010, vedi Associazione Calcio Salernitana Femminile. U.S.F. SalernitanaCalcio Le Granatine, le girls Segni distintivi Uniformi di gara Casa Trasferta Colori sociali Granata Simboli Ippocampo Dati societari Cittأ Salerno Nazione Italia Confederazione UEFA Federazione FIGC Fondazione 1971 Scioglimento1977 Stadio Stadio Donato Vestuti(9 000 posti) Palmarأ¨s Tito...

ذ—ذµذ¼رپذ؛ذ°رڈ ذ؟ذ¾ر‡ر‚ذ°ذ£ذµذ·ذ´ر‹ ذگذ»ذ°ر‚ر‹ر€رپذ؛ذ¸ذ¹ ذگذ»ذµذ؛رپذ°ذ½ذ´ر€ذ¸ذ¹رپذ؛ذ¸ذ¹ ذگذ½ذ°ذ½رŒذµذ²رپذ؛ذ¸ذ¹ ذگر€ذ´ذ°ر‚ذ¾ذ²رپذ؛ذ¸ذ¹ ذگر€ذ·ذ°ذ¼ذ°رپرپذ؛ذ¸ذ¹ ذگر‚ذ؛ذ°ر€رپذ؛ذ¸ذ¹ ذگر…ر‚ر‹ر€رپذ؛ذ¸ذ¹ ذ‘ذ°ذ»ذ°رˆذ¾ذ²رپذ؛ذ¸ذ¹ ذ‘ذ°ر…ذ¼رƒر‚رپذ؛ذ¸ذ¹ ذ‘ذµذ¶ذµر†ذ؛ذ¸ذ¹ ذ‘ذµذ»ذµذ±ذµذµذ²رپذ؛ذ¸ذ¹ ذ‘ذµذ»ذ¾ذ·ذµر€رپذ؛ذ¸ذ¹ ذ‘ذµر€ذ´رڈذ½رپذ؛ذ¸ذ¹ ذ‘ذ¾ذ±ر€ذ¾ذ²رپذ؛ذ¸ذ¹ ذ‘ذ¾ذ³ذ¾ر€ذ¾ذ´رپذ؛ذ¸ذ¹ ذ‘ذ¾ذ³رƒر‡ذ°ر€رپذ؛ذ¸ذ¹ ذ‘ذ¾ر€ذ¸رپذ¾ذ³ذ»ذµذ±رپذ؛ذ¸ذ¹ ذ‘ذ¾ر€ذ¾ذ²ذ¸ر‡رپذ؛ذ¸ذ¹ ذ‘ر€ذ¾ذ½ذ½ذ¸ر†ذ؛ذ¸ذ¹ ذ‘رƒذ³رƒذ»رŒذ¼ذ¸ذ½رپذ؛ذ¸ذ¹ ذ‘رƒï؟½...

German infantry division This article needs additional citations for verification. Please help improve this article by adding citations to reliable sources. Unsourced material may be challenged and removed.Find sources: Flemish Legion – news آ· newspapers آ· books آ· scholar آ· JSTOR (March 2010) (Learn how and when to remove this message) Flemish LegionSleeve insignia of the Flemish Legion, based on the traditional iconography of the Flemish Movement.Acti...

2016ه¹´ç¾ژهœ‹ç¸½çµ±éپ¸èˆ‰ ← 2012 2016ه¹´11وœˆ8و—¥ 2020 → 538ه€‹éپ¸èˆ‰ن؛؛هœکه¸ن½چçچ²ه‹éœ€270票و°‘و„ڈèھ؟وں¥وٹ•ç¥¨çژ‡55.7%[1][2] â–² 0.8 % èژ·وڈگهگچن؛؛ ه”گç´چآ·ه·و™® ه¸Œو‹‰èژ‰آ·ه…‹و—é “ و”؟ه…ڑ ه…±ه’Œé»¨ و°‘ن¸»ه…ڑ ه®¶é„‰ه· ç´گç´„ه· ç´گç´„ه· ç«é€‰وگو،£ è؟ˆه…‹آ·ه½و–¯ è’‚ه§†آ·ه‡±وپ© 选ن¸¾ن؛؛票 304[3][4][註 1] 227[5] 胜ه‡؛ه·/çœپ 30 + ç·¬-2 20 + DC و°‘éپ¸ه¾—票 62,984,828[6] 65,853,514[6]...

ظƒظٹظˆط¨ط³ ظƒظٹظˆط¨ط³طµظˆط±ط© ط§ظ„ظ…ظˆظ‚ط¹ ط§ظ„ط¥ظ„ظƒطھط±ظˆظ†ظٹ ط§ظ„ظ…ظˆظ‚ط¹ ط§ظ„ط±ط³ظ…ظٹطŒ ظˆط§ظ„ظ…ظˆظ‚ط¹ ط§ظ„ط±ط³ظ…ظٹطŒ ظˆط§ظ„ظ…ظˆظ‚ط¹ ط§ظ„ط±ط³ظ…ظٹ ط§ظ„ظ…طµظ†ط¹ ط¥ظٹط±ط¨ط§طµ ظ„ظ„ط¯ظپط§ط¹ ظˆط§ظ„ظپط¶ط§ط،[1] ط§ظ„ط·ط§ظ‚ظ… طںطںطں طھط§ط±ظٹط® ط§ظ„ط¥ط·ظ„ط§ظ‚ 18 ط¯ظٹط³ظ…ط¨ط± 2019[2] ط§ظ„طµط§ط±ظˆط® ط³ظˆظٹظˆط²-a2.1 [ظ„ط؛ط§طھ ط£ط®ط±ظ‰][2] ظ†ظ‚ط·ط© ط§ظ„طط¶ظٹط¶ 712 ظƒظٹظ„ظˆظ…طھط± ظ†ظ‚ط·ط© ط§ظ„ط£ظˆط¬ 715 ظƒظٹظ„ظˆظ…طھط±&#...

Artikel ini perlu dikembangkan agar dapat memenuhi kriteria sebagai entri Wikipedia.Bantulah untuk mengembangkan artikel ini. Jika tidak dikembangkan, artikel ini akan dihapus. Artikel ini membutuhkan rujukan tambahan agar kualitasnya dapat dipastikan. Mohon bantu kami mengembangkan artikel ini dengan cara menambahkan rujukan ke sumber tepercaya. Pernyataan tak bersumber bisa saja dipertentangkan dan dihapus.Cari sumber: Marah Halim Harahap – berita آ· surat kabar ï؟½...

Fund helping developing countries to counter climate change Green Climate FundAbbreviationGCFFormation2010; 14 years ago (2010)Legal statusActiveHeadquartersSongdo International Business District, Yeonsu-gu, Incheon, South KoreaWebsiteGreenClimate.fund The Green Climate Fund (GCF) is a fund for climate finance that was established within the framework of the United Nations Framework Convention on Climate Change (UNFCCC). Its objective is to assist developing countries with c...

و•™وœƒه¹´و›† è¥؟و–¹ ه°‡è‡¨وœں èپ–èھ•وœں(英è¯ï¼ڑChristmastide) ه¸¸ه¹´وœںه‰چو®µï¼ڈé،¯çڈ¾وœں ه››و—¬وœں èپ–週 逾è¶ٹ節ن¸‰و—¥و…¶ه…¸ ه¾©و´»وœں(英è¯ï¼ڑEastertide) ه¸¸ه¹´وœںه¾Œو®µï¼ڈèپ–éˆé™چ臨وœں و±و–¹ é™چ臨وœں èپ–èھ•وœں (ه¸¸ه¹´وœں) ه¤§é½‹é گه‚™وœں ه¤§é½‹وœں ه¾©و´»وœں ه®—ه¾’齋وœں (ه¸¸ه¹´وœں) ه°‡è‡¨وœںم€پé™چ臨وœںم€په¾…é™چ節(英èھï¼ڑAdvent,و‹‰ن¸پèھï¼ڑAdventus[註 1])وک¯هں؛ç£و•™و•™وœƒçڑ„é‡چè¦پ節وœں,وک¯ن¸؛ن؛†و…¶ç¥è€¶ç©Œèپ–èھ•ه‰چçڑ„و؛–ه‚™وœں與ç‰ه¾…وœںï؟½...

ط¨ط´ظٹط± ط§ظ„ط³طط¨ط§ظ†ظٹ ظ…ط¹ظ„ظˆظ…ط§طھ ط´ط®طµظٹط© ط§ظ„ظ…ظٹظ„ط§ط¯ 22 ط£ظƒطھظˆط¨ط± 1972 (ط§ظ„ط¹ظ…ط± 51 ط³ظ†ط©)ط¨ظ†ط²ط±طھ [ظ„ط؛ط§طھ ط£ط®ط±ظ‰] ظ…ط±ظƒط² ط§ظ„ظ„ط¹ط¨ ظ…ط¯ط§ظپط¹ ط§ظ„ط¬ظ†ط³ظٹط© طھظˆظ†ط³ ط§ظ„ظ…ط³ظٹط±ط© ط§ظ„ط§ططھط±ط§ظپظٹط©1 ط³ظ†ظˆط§طھ ظپط±ظٹظ‚ ظ…. (ظ‡ظ€.) ط§ظ„طھط±ط¬ظٹ ط§ظ„ط±ظٹط§ط¶ظٹ ط§ظ„طھظˆظ†ط³ظٹ ط§ظ„ظ†ط§ط¯ظٹ ط§ظ„ط±ظٹط§ط¶ظٹ ط§ظ„ط¨ظ†ط²ط±طھظٹ Espأ©rance Sportive de Tunis ط§ظ„ظ…ظ†طھط®ط¨ ط§ظ„ظˆط·ظ†ظٹ 1994–1999 طھظˆظ†ط³ 30 (0) ط§ظ„ظ…ظˆط§ظ‚ط¹ ظ…ظڈط¹ط±ظگظ‘ï؟½...

Japanese manga series by Shإ«ichi Shigeno and its franchise For other uses, see Initial D (disambiguation). Initial DFirst tankإچbon volume cover, featuring Takumi Fujiwara and the AE86é و–‡ه—(م‚¤مƒ‹م‚·مƒ£مƒ«) D(Inisharu Dؤ«)GenreAction[1]Coming-of-age[2]Sports[3] MangaWritten byShuichi ShigenoPublished byKodanshaEnglish publisherNA: Tokyopop (former)Kodansha USA (current)ImprintYoung Magazine KCMagazineWeekly Young MagazineDemographicSeinenOriginal runJuly...

Cet article est une أ©bauche concernant un cours d'eau de France et la Dordogne. Vous pouvez partager vos connaissances en l’amأ©liorant (comment ?) selon les recommandations des projets correspondants. Pour les articles homonymes, voir Vallأ©e (homonymie). la Vallأ©e La Vallأ©e أ Sagelat, en bordure du golf. Caractأ©ristiques Longueur 11,3 km Bassin collecteur la Dordogne Rأ©gime pluvial Cours آ· Localisation Saint-Laurent-la-Vallأ©e آ· Coordonnأ©es 44آ° 45′ 25″&#...

Sveriges ambassad i Paris BeskickningstypAmbassadFrأ¥nSverigeTillFrankrikeAdressBesأ¶ksadress:17, Rue Barbet-de-Jouy75007 Paris Postadress:Ambassade de Suأ¨de17, rue du Barbet de Jouy75007 Paris FrankrikeKoordinater48آ°51′12″N 2آ°19′04″أ– / 48.853349آ°N 2.317767آ°أ– / 48.853349; 2.317767BeskickningschefHأ¥kan أ…kesson (sedan 2020) Sveriges ambassad i Paris Sveriges ambassad i Paris أ¤r Sveriges diplomatiska beskickning i Frankrike som أ¤r belأ¤gen i landets huv...

American soccer player Rachel Van Hollebeke Rachel with the Gold Pride in September 2010Personal informationFull name Rachel Marie Buehler Van HollebekeBirth name Rachel Marie Buehler[1]Date of birth (1985-08-26) August 26, 1985 (age 39)Place of birth Del Mar, California, United StatesHeight 5 ft 5 in (1.65 m)Position(s) DefenderCollege careerYears Team Apps (Gls)2003–2007 Stanford Cardinal Senior career*Years Team Apps (Gls)2006–2008 San Diego WFC SeaLions 200...

PBM Mariner Mل»™t chiل؛؟c PBM-5 Mariner cل»§a Hل؛£i quأ¢n Hoa Kل»³ Kiل»ƒu Tأ u bay Nhأ chل؛؟ tل؛،o Martin Chuyل؛؟n bay ؤ‘ل؛§u 18 thأ،ng 2 nؤƒm 1939 Vأ o trang bل»‹ Thأ،ng 9, 1940 Thل؛£i loل؛،i 1964 (Uruguay) Sل» dل»¥ng chأnh Hل؛£i quأ¢n Hoa Kل»³ Bل؛£o vل»‡ Bل» biل»ƒn Hoa Kل»³ Khأ´ng quأ¢n Hoأ ng gia Australia Hل؛£i quأ¢n Argentina Giai ؤ‘oل؛،n sل؛£n xuل؛¥t 1937-1949[1] Sل»‘ lئ°ل»£ng sل؛£n xuل؛¥t 1.285 Biل؛؟n thل»ƒ Martin P5M Marlin Martin PBM Mariner lأ mل»™t loل؛،i tأ u bay nأ©...

Infanteriregemente 4 Hoch- und Deutschmeister paraderar 1896. Infanteriregemente 4 Hoch- und Deutschmeister i strid 1915. أ–sterrike-Ungerns krigsmakt (tyska: die Bewaffnete Macht), bestod av fyra komponenter: den gemensamma armأ©n, (tyska: 'k.u.k. Armee'); den gemensamma flottan, (tyska: 'k.u.k. Kriegsmarine'): den أ¶sterrikiska riksdelens armأ©, (tyska: 'k.k. Landwehr'); den ungerska riksdelens armأ©, (ungerska: Magyar Kirأ،lyi Honvأ©dsأ©g/tyska: k.u. Landwehr). Titulatur Titulaturen fأ¶r ...

Danish politician Stأ©n KnuthMayor of Slagelse MunicipalityIn office1 January 2014 – 31 December 2017Preceded byLis Tribler (A)Succeeded byJohn Dyrby Paulsen (A)Member of the FolketingIncumbentAssumed office 5 June 2019ConstituencyZealand Personal detailsBorn (1964-12-15) 15 December 1964 (age 59)Slagelse, DenmarkPolitical partyVenstre Stأ©n Knuth (born 15 December 1964 in Slagelse) is a Danish politician who is a member of the Folketing for the Venstre political party. He...
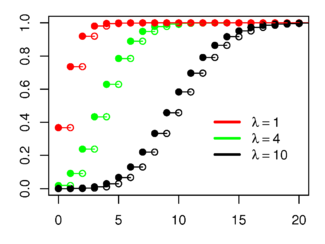










![{\displaystyle \lambda [1\!-\!\ln(\lambda )]\!+\!e^{-\lambda }\sum _{k=0}^{\infty }{\frac {\lambda ^{k}\ln(k!)}{k!}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/24650c837524f593a60e41f7371b39de75512d5c)




![{\displaystyle p_{X}[k]={\frac {\lambda ^{k}e^{-\lambda }}{k!}}\,\!}](https://wikimedia.org/api/rest_v1/media/math/render/svg/7577de95fa7357af0fd401dfd4b1cce27744cae9)

























