Nguyễn Khắc Nghiên
|
Read other articles:

Artikel atau bagian mungkin perlu ditulis ulang agar sesuai dengan standar kualitas Wikipedia. Anda dapat membantu memperbaikinya. Halaman pembicaraan dari artikel ini mungkin berisi beberapa saran. Artikel ini membutuhkan penyuntingan lebih lanjut mengenai tata bahasa, gaya penulisan, hubungan antarparagraf, nada penulisan, atau ejaan. Anda dapat membantu untuk menyuntingnya. artikel ini perlu dirapikan agar memenuhi standar Wikipedia. Tidak ada alasan yang diberikan. Silakan kembangkan arti...

Kerang batik Paphia undulata A view of a valve of Paratapes undulatus. Museum specimenTaksonomiKerajaanAnimaliaFilumMolluscaKelasBivalviaOrdoVeneroidaFamiliVeneridaeGenusPaphiaSpesiesPaphia undulata Ignaz von Born, 1778 lbs Paratapes undulatus, nama umum kerang batik, adalah spesies kerang air asin, moluska bivalvia laut dalam keluarga Veneridae, kerang batik.[1] Distribusi dan habitat Spesies ini menghuni dasar laut berpasir dangkal di Indo-Pasifik Barat (Laut Merah hingga Papua Nugi...

Artikel ini sebatang kara, artinya tidak ada artikel lain yang memiliki pranala balik ke halaman ini.Bantulah menambah pranala ke artikel ini dari artikel yang berhubungan atau coba peralatan pencari pranala.Tag ini diberikan pada Maret 2023. El juego del ahorcadoSutradaraManuel Gómez PereiraSkenarioManuel Gómez PereiraSalvador García RuizBerdasarkanEl juego del ahorcadooleh Imma TurbauPemeranClara LagoÁlvaro CervantesAdriana UgarteAbel FolkVictoria PagésVíctor ValdiviaBoris RuizÀngels...

Putri Duyung dan 1001 Keajaiban Season 2Genre Drama Fantasi Komedi PembuatLunar FilmSkenarioTeam LunarSutradaraBobby HerlambangPemeran Queen Gendis Kia Poetri Tyas Mirasih Amel Alvi Nay Nanoy Winona Karamoy Farah Cute Karen Kristy Ucup Gembul Bilal Pitung Obinna Cleo Haura Saleh Ali Risma Nilawati Peppy Papham Nina Tutacha Bunbun Melly Penggubah lagu temaEross CandraLagu pembukaMelompat Lebih Tinggi — Sheila on 7Lagu penutupMelompat Lebih Tinggi — Sheila on 7Penata musikAry LogamNe...

العلاقات الكازاخستانية الليسوتوية كازاخستان ليسوتو كازاخستان ليسوتو تعديل مصدري - تعديل العلاقات الكازاخستانية الليسوتوية هي العلاقات الثنائية التي تجمع بين كازاخستان وليسوتو.[1][2][3][4][5] مقارنة بين البلدين هذه مقارنة عامة ومرجعية ل�...
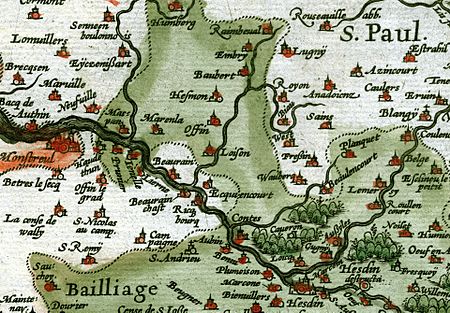
Commune in Hauts-de-France, FranceRoyonCommuneRebuilt château Coat of armsLocation of Royon RoyonShow map of FranceRoyonShow map of Hauts-de-FranceCoordinates: 50°28′25″N 1°59′35″E / 50.4736°N 1.9931°E / 50.4736; 1.9931CountryFranceRegionHauts-de-FranceDepartmentPas-de-CalaisArrondissementMontreuilCantonFrugesIntercommunalityCC Haut Pays du MontreuilloisGovernment • Mayor (2020–2026) Jean-Marie Cornuel[1]Area17.49 km2 (2.89&...

United States historic placeHickman County CourthouseU.S. National Register of Historic Places Show map of KentuckyShow map of the United StatesLocationCourt Sq., Clinton, KentuckyCoordinates36°40′00″N 88°59′39″W / 36.66667°N 88.99417°W / 36.66667; -88.99417 (Hickman County Courthouse)Area1 acre (0.40 ha)Built1884ArchitectMcDonald BrothersNRHP reference No.75000767[1]Added to NRHPSeptember 11, 1975 The Hickman County Courthou...

Concours Eurovision de la chanson 2006 Feel The Rhythm Dates Demi-finale 18 mai 2006 Finale 20 mai 2006 Retransmission Lieu OAKA Indoor Hall Complexe olympique d'Athènes, Athènes Grèce Présentateur(s) Maria Menounos Sákis Rouvás Superviseur exécutif Svante Stockselius Télédiffuseur hôte ERT Ouverture Demi-finale : Medley et Love Shine a Light par Maria Menounos et Sákis Rouvás Finale : The Song of Life par Foteini Darra et My Number One par Helena Paparizou Entracte Dem...

Artikel ini tidak memiliki referensi atau sumber tepercaya sehingga isinya tidak bisa dipastikan. Tolong bantu perbaiki artikel ini dengan menambahkan referensi yang layak. Tulisan tanpa sumber dapat dipertanyakan dan dihapus sewaktu-waktu.Cari sumber: Islam di Djibouti – berita · surat kabar · buku · cendekiawan · JSTOR Islam menurut negara Afrika Aljazair Angola Benin Botswana Burkina Faso Burundi Kamerun Tanjung Verde Republik Afrika Tengah Chad Kom...

Peeni HenareHenare pada 2019 Menteri Pertahanan ke-41PetahanaMulai menjabat 6 November 2020Perdana MenteriJacinda ArdernPendahuluRon MarkPenggantiPetahanaMenteri Whānau Ora ke-3PetahanaMulai menjabat 26 Oktober 2017Perdana MenteriJacinda ArdernPendahuluTe Ururoa FlavellPenggantiPetahanaMenteri Pemuda ke-14Masa jabatan26 Oktober 2017 – 6 November 2020Perdana MenteriJacinda ArdernPendahuluNikki KayePenggantiPriyanca RadhakrishnanMenteri Pertahanan Sipil ke-26Masa jabatan27 J...

Oberlargcomune Oberlarg – Veduta LocalizzazioneStato Francia RegioneGrand Est Dipartimento Alto Reno ArrondissementAltkirch CantoneAltkirch TerritorioCoordinate47°27′N 7°14′E / 47.45°N 7.233333°E47.45; 7.233333 (Oberlarg)Coordinate: 47°27′N 7°14′E / 47.45°N 7.233333°E47.45; 7.233333 (Oberlarg) Superficie8,11 km² Abitanti157[1] (2009) Densità19,36 ab./km² Altre informazioniCod. postale68480 Fuso orarioUTC+1 Codice ...

This template was considered for deletion on 29 October 2011. The result of the discussion was no consensus. Animation: American / Canadian / Television Template‑class Animation portalThis template is within the scope of WikiProject Animation, a collaborative effort to build an encyclopedic guide to animation on Wikipedia. If you would like to participate, you can edit the article attached to this page, help out with the open tasks, or contribute to the discussion.AnimationWikipedia:WikiPro...

Сельское поселение России (МО 2-го уровня)Новотитаровское сельское поселение Флаг[d] Герб 45°14′09″ с. ш. 38°58′16″ в. д.HGЯO Страна Россия Субъект РФ Краснодарский край Район Динской Включает 4 населённых пункта Адм. центр Новотитаровская Глава сельского пос�...

Non-orientable surface with one edge A Möbius strip made with paper and adhesive tape In mathematics, a Möbius strip, Möbius band, or Möbius loop[a] is a surface that can be formed by attaching the ends of a strip of paper together with a half-twist. As a mathematical object, it was discovered by Johann Benedict Listing and August Ferdinand Möbius in 1858, but it had already appeared in Roman mosaics from the third century CE. The Möbius strip is a non-orientable surface, meani...

Use of certain images and symbols which are designed to represent aspects of fascism Part of a series onFascism Principles Actual idealism Aestheticization of politics Anti-communism Anti-intellectualism Anti-materialism Anti-pacifism Authoritarianism Chauvinism Class collaboration Conspiracism Corporatism Cult of personality Dictatorship Direct action Dirigisme Eugenics Heroic capitalism Heroic realism Heroism Imperialism Indoctrination Interventionism Economic Social Irrationalism Machismo ...

Political party in Syria This article is about the branch that controls Syria. For the pan-Arab Ba'ath Party, which is Syrian-led but has branches in multiple countries, see Ba'ath Party (Syrian-dominated faction). Arab Socialist Ba'ath Party – Syria Region حزب البعث العربي الاشتراكي – قطر سورياGoverning bodyCentral Command (from 2018)[1]General SecretaryBashar al-AssadAssistant General SecretaryIbrahim al-Hadid[2][3]Founded7 Apr...

French economist This article needs additional citations for verification. Please help improve this article by adding citations to reliable sources. Unsourced material may be challenged and removed.Find sources: Edmond Malinvaud – news · newspapers · books · scholar · JSTOR (March 2015) (Learn how and when to remove this message) Edmond MalinvaudEdmond Malinvaud (right), next to Yves Balasko (center) and Gérard Debreu, in 1977Born(1923-04-25)25 April ...

Political party in the United States Liberal Party USA ChairmanTrisha ButlerFoundedDecember 3, 2022 (as Association of Liberty State Parties)February 12, 2024 (as Liberal Party USA)Split fromLibertarian PartyMembership (2024)31,343IdeologyClassical liberalismWebsitewww.liberalpartyusa.orgPolitics of United StatesPolitical partiesElections Liberal Party USA (formerly known as Association of Liberty State Parties) is a liberal political party in the United States that is affiliated with mu...

English creole spoken in Papua New Guinea Tok PisinPronunciation[tok pisin][1]Native toPapua New GuineaNative speakers130,000 (2004–2016)[2]L2 speakers: 4,000,000[2]Language familyEnglish Creole PacificMelanesian PidginTok PisinWriting systemLatin script (Tok Pisin alphabet)Pidgin BrailleOfficial statusOfficial language in Papua New GuineaLanguage codesISO 639-2tpiISO 639-3tpiGlottologtokp1240Linguasphere52-ABB-ccThis article contains IPA ...

Tournoi de Wimbledon 1878 Édition Lawn-Tennis Championship[1] Lieu All England Club Wimbledon 51° 26′ 01″ N, 0° 12′ 51″ O Catégorie Grand Chelem[a] Surface Gazon (ext.) Tableaux de simple Messieurs 6 tours (34 joueurs) Frank Hadow Tournoi de Wimbledon Édition 1877 Édition 1879 Localisation Géolocalisation sur la carte : Royaume-Uni localisation Géolocalisation sur la carte : Angleterre localisation modifier Le tournoi de Wimbledon...
