Nguyên tử heli
| |||||||||||||||||||||||||||||||||||||||||||||||||||||
Read other articles:

Magazine financed by the European Development Fund The CourierEditor-in-ChiefHegel GoutierStaff writersDebra Percival, Marie-Martine BuckensFrequencyBi-monthlyCirculation80,000[1]PublisherEuropean CommissionFirst issueJuly 2007 (n. 1-New Edition)Final issueJuly 2011 n. 24CompanyGOPA-CartermillCountryBelgiumBased inBrusselsLanguageEnglish, French, Spanish, PortugueseISSN1784-682X The Courier logo. The Courier was an ACP-EU development magazine published by the Development Directorate G...

Keuskupan Agung NankingArchidioecesis Nanchinensis天主教南京总教区Katedral Bunda Tak Bernoda, NanjingLokasiNegaraChinaProvinsi gerejawiNanjingKoordinat32°02′41″N 118°46′42″E / 32.044751°N 118.778343°E / 32.044751; 118.778343Koordinat: 32°02′41″N 118°46′42″E / 32.044751°N 118.778343°E / 32.044751; 118.778343StatistikPopulasi- Total- Katolik(per 1949)6.000.000 [1]32,536 [1] (0.5%)...

For other uses, see Marbach. The mare's well horse fountain at Marbach, featuring an Arabian mare and foal. Marbach stables The Marbach Stud, German: Haupt- und Landgestüt Marbach, is Germany's oldest state stud farm for horse breeding, has a history that dates back over 500 years. It is located in southwest Germany near Gomadingen in the Reutlingen district of Baden-Württemberg. The annual stallion parade is an internationally known attraction, and the stud hosts over 500,000 visitors per ...

Bendera Maroko Perbandingan 2:3 Dipakai 17 November 1915 Bendera Maroko terdiri dari sebuah bintang berwarna hijau pada sebuah latar belakang berwarna merah. Bendera baru ini ditampilkan pada hari kemerdekaan Maroko pada tahun 1956. Pada abad ke-17 bendera ini digunakan oleh Dinasti Alawi. Bendera bersejarah Bendera Maroko pada masa Dinasti Idrisid Bendera Maroko pada masa Dinasti Almoravid Bendera Maroko pada masa Kekhalifahan Almohad Bendera Maroko pada masa Dinasti Marinid Bendera Maroko ...
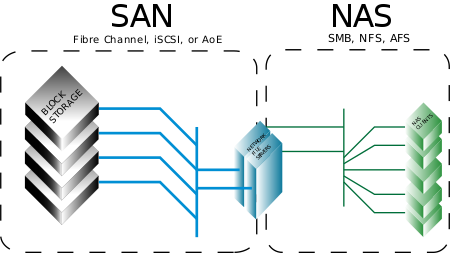
Pour les articles homonymes, voir SAN. Protocoles d'accès à un SAN. En informatique, un réseau de stockage, ou SAN (de l'anglais Storage Area Network), est un réseau spécialisé permettant de mutualiser des ressources de stockage. Définition Différence entre SAN et NAS. Un réseau de stockage se différencie des autres systèmes de stockage tels que le NAS (Network attached storage) par un accès bas niveau aux disques. Pour simplifier, le trafic sur un SAN est très similaire aux pri...

ロバート・デ・ニーロRobert De Niro 2011年のデ・ニーロ生年月日 (1943-08-17) 1943年8月17日(80歳)出生地 アメリカ合衆国・ニューヨーク州ニューヨーク市身長 177 cm職業 俳優、映画監督、映画プロデューサージャンル 映画、テレビドラマ活動期間 1963年 -配偶者 ダイアン・アボット(1976年 - 1988年)グレイス・ハイタワー(1997年 - )主な作品 『ミーン・ストリート』(1973年)...

Shimonoseki 下関市Kota inti BenderaLambangLokasi Shimonoseki di Prefektur YamaguchiNegara JepangWilayahChūgokuPrefektur YamaguchiPemerintahan • Wali kotaShintarō MaedaLuas • Total716 km2 (276 sq mi)Populasi (Oktober 1, 2015) • Total268.517 • Kepadatan375,0/km2 (9,700/sq mi)Zona waktuUTC+9 (JST)Kode pos750-8521Simbol • PohonCinnamomum camphora• BungaCrinum asiaticum• Pohon berbunga...

Шалфей обыкновенный Научная классификация Домен:ЭукариотыЦарство:РастенияКлада:Цветковые растенияКлада:ЭвдикотыКлада:СуперастеридыКлада:АстеридыКлада:ЛамиидыПорядок:ЯсноткоцветныеСемейство:ЯснотковыеРод:ШалфейВид:Шалфей обыкновенный Международное научное наз...

County in North Carolina, United States Not to be confused with Asheville, North Carolina or Asheboro, North Carolina. County in North CarolinaAshe CountyCountyAshe County Courthouse in Jefferson FlagSealLocation within the U.S. state of North CarolinaNorth Carolina's location within the U.S.Coordinates: 36°26′N 81°30′W / 36.44°N 81.50°W / 36.44; -81.50Country United StatesState North CarolinaFounded1799Named forSamuel AsheSeatJeffersonLargest communi...

This article needs additional citations for verification. Please help improve this article by adding citations to reliable sources. Unsourced material may be challenged and removed.Find sources: Julius Henry, Duke of Saxe-Lauenburg – news · newspapers · books · scholar · JSTOR (December 2009) (Learn how and when to remove this message) Duke of Saxe-Lauenburg Julius HenryDuke of Saxe-LauenburgReign1656 – 1665PredecessorAugustusSuccessorFrancis Erd...

Запрос «Пугачёва» перенаправляется сюда; см. также другие значения. Алла Пугачёва На фестивале «Славянский базар в Витебске», 2016 год Основная информация Полное имя Алла Борисовна Пугачёва Дата рождения 15 апреля 1949(1949-04-15) (75 лет) Место рождения Москва, СССР[1]...

Baked corn snack This article is about the snack sold under the Walkers and Smiths brands. For snacks of this name from other companies and other uses, see Monster Munch (disambiguation). Monster Munch pickled onion flavour Monster Munch are a British baked corn snack created by Smiths in 1977 and manufactured by Walkers. They are aimed at children and widely consumed in the United Kingdom.[1] Flavours include Roast Beef, Pickled Onion and Sweet and Spicy Flamin' Hot.[2] On th...

此條目可参照英語維基百科相應條目来扩充。 (2021年5月6日)若您熟悉来源语言和主题,请协助参考外语维基百科扩充条目。请勿直接提交机械翻译,也不要翻译不可靠、低品质内容。依版权协议,译文需在编辑摘要注明来源,或于讨论页顶部标记{{Translated page}}标签。 约翰斯顿环礁Kalama Atoll 美國本土外小島嶼 Johnston Atoll 旗幟颂歌:《星條旗》The Star-Spangled Banner約翰斯頓環礁�...

French politician (born 1947) Hubert VédrineHubert Védrine in 2006Minister of Foreign AffairsIn office4 June 1997 – 6 May 2002Prime MinisterLionel JospinPreceded byHervé de CharetteSucceeded byDominique de VillepinSecretary General to the President of FranceIn office17 May 1991 – 17 May 1995PresidentFrançois MitterrandPreceded byJean-Louis BiancoSucceeded byDominique de VillepinSpokesperson of the PresidentIn office24 May 1988 – 17 May 1991PresidentFranço...

British journalist & writer (born 1968) This article is about a British journalist. For the Australian linguist, see Luke Harding (linguist). Luke HardingBorn21 April 1968 Nottingham (United Kingdom) Alma materUniversity College, Oxford OccupationJournalist, writer, foreign correspondent EmployerThe Guardian (1996–) WorksMafia State, The Snowden Files, WikiLeaks: Inside Julian Assange's War on Secrecy AwardsJames Cameron Memorial Trust Award (2014)...

Italian botanist De Notaris Giuseppe De Notaris (18 April 1805, Milan – 22 January 1877) was an Italian botanist generally known for his work with cryptogams native to Italy. He studied medicine at the University of Pavia, obtaining his medical degree in 1830. Having developed an interest in botany, by 1832 he had abandoned the field of medicine. In 1836 he accepted an assignment at the botanical garden in Turin, and a few years later, was named professor of botany and director of the botan...

烏克蘭總理Прем'єр-міністр України烏克蘭國徽現任杰尼斯·什米加尔自2020年3月4日任命者烏克蘭總統任期總統任命首任維托爾德·福金设立1991年11月后继职位無网站www.kmu.gov.ua/control/en/(英文) 乌克兰 乌克兰政府与政治系列条目 宪法 政府 总统 弗拉基米尔·泽连斯基 總統辦公室 国家安全与国防事务委员会 总统代表(英语:Representatives of the President of Ukraine) 总...

عنتطواف إفريقيا للدراجات 2020▷ 20192021 ◁سباقات تور دو فاسو طواف السنغال [الفرنسية] لا تروبيكال أميسا بونغو طواف رواندا فائزون داريل إيمبي الفائز حسب التصنيف العام خيارات العرض الأولية يُمكن استخدام وسيط |وضع= لضبط خيارات عرض القالب الأوليّة: |وضع=collapsed: {{طواف إفريقيا لل...
「贝南」重定向至此。关于其他用法,请见「贝南 (消歧义)」。 贝宁共和国République du Bénin(法語) 国旗 国徽 格言:Fraternité, Justice, Travail(法语)“友谊、正义、劳动”国歌:L'Aube Nouvelle《新的黎明》首都波多诺伏中央政府所在地科托努最大行政区阿黎博里省最大城市科托努官方语言法語官方文字法語族群38.4% 豐族15.1% 阿賈(英语:Adja people) & 格恩12% 约鲁...

Mathematical software Symbolic algebra redirects here. For the algebra of logic, see Symbolical algebra. A computer algebra system (CAS) or symbolic algebra system (SAS) is any mathematical software with the ability to manipulate mathematical expressions in a way similar to the traditional manual computations of mathematicians and scientists. The development of the computer algebra systems in the second half of the 20th century is part of the discipline of computer algebra or symbolic computa...








![{\displaystyle H\Psi ({\vec {r}}_{1},\,{\vec {r}}_{2})={\Bigg [}-{\frac {1}{2}}\nabla _{r_{1}}^{2}-{\frac {1}{2}}\nabla _{r_{2}}^{2}-{\frac {Z}{r_{1}}}-{\frac {Z}{r_{2}}}+{\frac {1}{r_{12}}}{\Bigg ]}\Psi ({\vec {r}}_{1},\,{\vec {r}}_{2})}](https://wikimedia.org/api/rest_v1/media/math/render/svg/3ac54dc27c189ec94c4f1d45f256bf4b2b483467)















![{\displaystyle E_{n_{1},n_{2}}^{(0)}=E_{n_{1}}+E_{n_{2}}=-{\frac {Z^{2}}{2}}{\Bigg [}{\frac {1}{n_{1}^{2}}}+{\frac {1}{n_{2}^{2}}}{\Bigg ]}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/49c9aa07b4f54e2bfc4a0574de36c9cd7cd178e3)




![{\displaystyle \psi _{\pm }^{(0)}({\vec {r}}_{1},{\vec {r}}_{2})={\frac {1}{\sqrt {2}}}[\psi _{n_{1},l_{1},m_{1}}({\vec {r}}_{1})\psi _{n_{2},l_{2},m_{2}}({\vec {r}}_{2})\pm \psi _{n_{2},l_{2},m_{2}}({\vec {r}}_{1})\psi _{n_{1},l_{1},m_{1}}({\vec {r}}_{2})]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/c4397a65d19f8e9993dcd98c4edf34bcc41a4d68)























