Фізика полімерів
|
Read other articles:

Pemandangan Front-de-Seine dilihat dari Jembatan Bir-Hakeim Front-de-Seine merupakan sebuah wilayah di Paris, Prancis, yang terletak di sepanjang Sungai Arondisemen ke-15 Paris, di ujung Menara Eiffel.[1] Wilayah ini termasuk salah satu konsentrasi bangunan tinggi terbesar di kota. Secara administratif, wilayah ini dibagi antara distrik-distrik[2] Javel dan Grenelle. Pusat perbelanjaan yang baru dirancang ulang, Centre commercial Beaugrenelle dibuka pada tahun 2013.[3]...

The cover art for the first volume of the anime series, published by Aniplex, featuring the main characters Ghost Stories (学校の怪談, Gakkō no Kaidan), also known as Ghosts at School, is a 2000 Japanese anime series directed by Noriyuki Abe and produced by Pierrot. The 20-episode series was adapted from Tōru Tsunemitsu's eponymous novel series. The series is based around the lives of five school children—Satsuki Miyanoshita, Keiichirō Miyanoshita, Hajime Aoyama, Reo Kakinoki, and ...

Halaman ini memuat daftar gunung di Pulau Kalimantan . Daftar ini tidak dimaksudkan sebagai suatu daftar yang lengkap atau selalu terbarui. Jika Anda melihat artikel yang seharusnya tercantum di sini, silakan sunting halaman ini dan tambahkan pranala ke artikel tersebut. Gunakan perubahan terkait untuk melihat perubahan terbaru dari artikel-artikel yang tercantum pada halaman ini.. Daftar gunung di Kalimantan Gunung Asing (1.703 m) Gunung Aurbunak (1.150 m) Gunung Balayan (1.599 m) Gunung Ban...

Cycling championships 2019 UEC European Track ChampionshipsVenueApeldoorn, NetherlandsDate(s)16–20 OctoberVelodromeOmnisport ApeldoornEvents22 (11 women, 11 men)← 20182020 → The 2019 UEC European Track Championships was the tenth edition of the elite UEC European Track Championships in track cycling and took place at the Omnisport Apeldoorn in Apeldoorn, Netherlands, between 16 and 20 October 2019.[1] The event was organised by the European Cycling Union. All E...

1800 Massachusetts's 10th congressional district special election ← 1798–1799 August 25, 1800 (first round)October 20, 1800 (runoff) 1800–1801 → Massachusetts's 10th congressional district Nominee Nathan Read Jacob Crowninshield Party Federalist Democratic-Republican Popular vote 1,567 1,364 Percentage 53.5% 46.5% U.S. Representative before election Samuel Sewall Federalist Elected U.S. Representative Nathan Read Federalist Elections in Massachusetts Gen...

2023 World Short Track Speed Skating ChampionshipsVenueMokdong Ice RinkLocationSeoul, South KoreaDates10–12 MarchCompetitors160 from 34 nations← Montréal 2022Rotterdam 2024 → The 2023 World Short Track Speed Skating Championships were held from 10 to 12 March 2023 in Seoul, South Korea.[1][2] Seoul were originally scheduled to host the 2020 Championships, but they were cancelled due to the COVID-19 pandemic. Medal summary Medal table &#...

Федеральное агентство по делам Содружества Независимых Государств, соотечественников, проживающих за рубежом, и по международному гуманитарному сотрудничествусокращённо: Россотрудничество Общая информация Страна Россия Юрисдикция Россия Дата создания 6 сентября...

هذه المقالة يتيمة إذ تصل إليها مقالات أخرى قليلة جدًا. فضلًا، ساعد بإضافة وصلة إليها في مقالات متعلقة بها. (أكتوبر 2023) هذه مقالة غير مراجعة. ينبغي أن يزال هذا القالب بعد أن يراجعها محرر؛ إذا لزم الأمر فيجب أن توسم المقالة بقوالب الصيانة المناسبة. يمكن أيضاً تقديم طلب لمراجعة ...

متحف الرقةمعلومات عامةنوع المبنى متحف المنطقة الإدارية الرقة البلد سوريا أبرز الأحداثالافتتاح الرسمي 1981 معلومات أخرىموقع الويب cdli.ucla.edu… الإحداثيات 35°56′45″N 39°01′00″E / 35.9458°N 39.0167°E / 35.9458; 39.0167 تعديل - تعديل مصدري - تعديل ويكي بيانات 35°56′45″N 39°1′00″E / ...

German state (1918–1945) Republic of BadenRepublik BadenState of Germany1918–1945 Flag Coat of arms The Republic of Baden (red) within the Weimar RepublicAnthemBadnerliedCapitalKarlsruheArea • 1925[1]15,070 km2 (5,820 sq mi)Population • 1925[1] 2,312,462 Government • TypeRepublicPresident • 1918–1920 (first) Anton Geiß• 1933–1945 (last) Walter Köhler (Minister-President) Reichsstatthalter •&...

Toy franchise owned by Hasbro For the 1995 television series, see Littlest Pet Shop (1995 TV series). For the 2012 television series, see Littlest Pet Shop (2012 TV series). For the video game, see Littlest Pet Shop (video game). Littlest Pet ShopTypeFigurineInventor(s)KennerCompanyKenner (Former)Hasbro (Current)Basic Fun! (Under license)CountryUnited StatesAvailability1992–presentMaterialsRubber (earlier pets were made up of plastic)SloganHow big is your Littlest Pet Shop? (2005–2012)Lit...

Cet article est une ébauche concernant la biologie cellulaire et moléculaire. Vous pouvez partager vos connaissances en l’améliorant (comment ?) selon les recommandations des projets correspondants. Figure comparant les effets de l'exposition à des agents génotoxiques (aneugènes et clastogènes) sur l'ADN. Les aneugènes induisent une mauvaise ségrégation des chromosomes dans les cellules filles, tandis que les clastogènes cassent l'ADN et les chromosomes. Un clastogène est ...
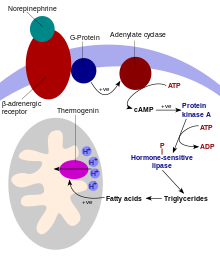
Process of heat production within organisms Not to be confused with thermogeneration. This article needs additional citations for verification. Please help improve this article by adding citations to reliable sources. Unsourced material may be challenged and removed.Find sources: Thermogenesis – news · newspapers · books · scholar · JSTOR (February 2007) (Learn how and when to remove this message) Thermogenesis is the process of heat production in orga...

Mrs. G. W. Denney Jane Franklin Hommel Denney (1878–1946), clubwoman, was president of the Tennessee Federation of Women's Clubs, in Knoxville, Tennessee, US. Biography She was born May 12, 1878, as Jane Franklin Hommel, the daughter of Daniel C. Hommel and Sarah Havely of Knoxville, Tennessee. She attended East Tennessee Institute for her education. She married George W. Denney on October 3, 1899; they had one son, Joseph F. Denney. Mrs. Denney was a member of the Suffrage Club of Knoxvil...

Presidential election in Sri Lanka in 1988 1988 Sri Lankan presidential election ← 1982 19 December 1988 1993 → Turnout55.32% 25.74 pp Nominee Ranasinghe Premadasa Sirimavo Bandaranaike Party UNP SLFP Popular vote 2,569,199 2,289,860 Percentage 50.43% 44.95% Winners of polling divisions. Premadasa in green, Bandaranaike in blue and Abeygunasekera in red. President before election J. R. Jayewardene UNP Elected President Ranasinghe Premadasa UNP Presidential el...

Czech animator and illustrator (1912–1969) For the soccer player, see Jiří Trnka (footballer). This article should specify the language of its non-English content, using {{lang}}, {{transliteration}} for transliterated languages, and {{IPA}} for phonetic transcriptions, with an appropriate ISO 639 code. Wikipedia's multilingual support templates may also be used - notably cs for Czech. See why. (March 2022) Jiří TrnkaTrnka...

У этого термина существуют и другие значения, см. Ганимед (значения). Ганимед Спутник Изображение Ганимеда, снятое JunoCam КА «Юнона». Светлые поверхности, следы недавних ударных столкновений, изборождённая поверхность и белая северная полярная шапка (в верхнем правом углу �...

2009 studio album by Deströyer 666DefianceStudio album by Deströyer 666Released22 June 2009 (Europe)14 July 2009 (USA)GenreBlackened thrash metalLength41:27LabelSeason of MistDeströyer 666 chronology Terror Abraxas(2003) Defiance(2009) Defiance is Deströyer 666's fourth full-length studio album. Professional ratingsReview scoresSourceRatingAllmusic[1]Blabbermouth linkMetal HammerNottingham Evening Postpositive[2] Track listing Weapons of Conquest - 03:03 I Am Not ...

Para otros usos de este término, véase Barrio (desambiguación).Shibuya, es uno de los 23 barrios especiales de Tokio. La Boca, uno de los barrios de Buenos Aires. Un barrio (del árabe hispánico bárri, ‘exterior’, y este del árabe برّيّ [barrī ], ‘salvaje’[1]) o colonia (en países que fueron parte del Virreinato de Nueva España), es toda subdivisión, con identidad propia, de una ciudad, pueblo o parroquia / corregimiento. Su origen puede ser una decisión admi...

Kreischa Huy hiệuVị trí của Kreischa Kreischa Quốc giaĐứcBangSachsenVùng hành chínhDresdenHuyệnSächsische Schweiz-OsterzgebirgePhân chia hành chính14Chính quyền • Thị trưởngFrank SchöningDiện tích • Tổng cộng28,97 km2 (1,119 mi2)Độ cao257 m (843 ft)Dân số (2006-12-31) • Tổng cộng4.441 • Mật độ1,5/km2 (4,0/mi2)Múi giờCET (UTC+01:00) • M...