Узагальнене перетворення Гафа
|
Read other articles:

Pulau Palm, juga dikenal sebagai Pulau Palm Raya, atau dengan nama Aborigin Bukaman,[1] merupakan sebuah pulau tropis dengan penduduk yang berjumlah 2.000 orang. Pemukiman ini dinamai Palm Island, the Mission, Palm Island Settlement atau Palm Community.[2] Pulau tersebut terletak 65 kilometer baratlaut Townsville, di pantai timur Queensland, Australia, 800 km utara garis balik selatan. Merupakan pulau utama dari kumpulan Palm Raya, dan meliputi teluk kecil, pantai berpasi...

Permainan pérépét jéngkol Lagu Permainan Sunda adalah lagu anak-anak sunda ketika mereka bermain, Lagu permainan sunda ini merupakan golongan lagu yang biasa dinyanyikan oleh anak-anak sambil bermain, baik dilakukan di dalam rumah, maupun di luar rumah waktu siang hari dalam keadaan cerah, atau di tempat lain tempat mereka bermain yang meneurut mereka nyaman biasanya di lapangan terbuka.[1] Bait-bait lagunya merupakan nyanyian bersama yang bersifat anonim, biasanya tidak semua da�...

Andrew Clyde Andrew Clyde (lahir 22 November 1963)[1] adalah seorang politikus dan pengusaha Amerika Serikat dari negara bagian Georgia. Berasal dari Partai Republik, Clyde merupakan anggota DPR. Referensi ^ Bowden, John (November 30, 2020). Rep.-elect Andrew Clyde (R-Ga.-09). The Hill. Diakses tanggal December 1, 2020. Pranala luar Representative Andrew Clyde, official U.S. House website Campaign website Biografi di Biographical Directory of the United States Congress Catatan s...

Denisonia Denisonia maculata (en) TaksonomiKerajaanAnimaliaFilumChordataKelasReptiliaOrdoSquamataFamiliElapidaeGenusDenisonia Krefft, 1869 DistribusiEndemikAustralia lbs Denisonia adalah nama genus yang terdiri dari dua spesies Elapidae endemik Australia. Nama genus ular ini diperoleh dari nama belakang anggota pemerintah di Australia pada abad ke-19 bernama William Thomas Denison.[1] Klasifikasi Denisonia devisi (WAITE & LONGMAN, 1920) Denisonia maculata (STEINDACHNER, 1867) Refe...

Politeknik Negeri Ujung PandangLogo PNUPNama sebelumnyaPoliteknik Universitas HasanuddinJenisPerguruan Tinggi Negeri Politeknik NegeriDidirikan1987DirekturProf. Ir. Muhammad Anshar, M.Si., Ph.D.Jumlah mahasiswa3.424 orangLokasiKota Makassar, Sulawesi Selatan, IndonesiaAlamatJl. Perintis Kemerdekaan KM. 10 (Kampus I) Jl. Tamalanrea Raya (BTP) (Kampus II)Warna HitamNama julukanKampus Hitam, Poltek, PNUPSitus webhttp://www.poliupg.ac.id/ Politeknik Negeri Ujung Pandang atau biasa disingkat...

Katedral Etchmiadzin di Armenia, dianggap Katedral pertama, yang secara tradisional diyakini dibangun pada 301 M (sekarang kebanyakan strukturnya berasal dari 483 M). Arsitektur katedral, basilika dan gereja dikarakteristikkan oleh skala besar bangunan dan mengikuti salah satu tradisi cabang dari bentuk, fungsi dan gaya yang semuanya bermula dari tradisi arsitektural Gereja Perdana yang didirikan pada Konstantinian. Katedral, serta beberapa gereja dan basilika memiliki bentuk struktural kompl...

Tindik nostrilTindik septum Tindik hidung adalah suatu tindik yang dibuat pada kulit atau tulang rawan yang membentuk struktur hidung manusia, biasanya untuk dipasangi perhiasan seperti anting, plug, atau aksesoris lainnya. Tindik hidung yang populer yaitu di bagian cuping hidung, melewati nostril (lubang hidung). Jenis tindik lainnya yaitu di bagian septum nasal, yaitu tulang rawan yang memisahkan lubang hidung kanan dan kiri. Antropologi Tindik hidung merupakan modifikasi tubuh yang populer...

Holly SampsonSampson berpose di film guru seks pertamakuLahirHolly Joy Sampson[1]4 September 1973 (umur 50)[1]Prescott, Arizona, A.S.[1]Nama lainNicolette[1]Nicolete[1]Nicolette Foster[1]Andrea Michaels[1]Zoe[1]Tinggi5 ft 5 in (1,65 m)[1] Holly Joy Sampson (lahir 4 September 1973), juga dikenl dengans sebutan Nicolette Foster, Andrea Michaels atau Zoe[1] adalah seorang aktris dan model as...

Etruscan hypogeum (burial chamber) in Tarquinia, Italy For the moon also designated Orcus I, see Vanth (moon). A diagram of the Tomb of Orcus, showing the two chambers and two dromes (entrances). The Tomb of Orcus (Italian: Tomba dell'Orco), sometimes called the Tomb of Murina (Italian: Tomba dei Murina), is a 4th-century BC Etruscan hypogeum (burial chamber) in Tarquinia, Italy. Discovered in 1868, it displays Hellenistic influences in its remarkable murals, which include the portrait of Vel...

Artikel ini sebatang kara, artinya tidak ada artikel lain yang memiliki pranala balik ke halaman ini.Bantulah menambah pranala ke artikel ini dari artikel yang berhubungan atau coba peralatan pencari pranala.Tag ini diberikan pada Februari 2023. MIS Al MunirMadrasah Ibtidaiyah Swasta Al MunirInformasiJenisSwastaAlamatLokasiJl. Ahmad I Kel. Makasar, Jakarta Timur, DKI Jakarta, IndonesiaSitus webMIS Al Munir pada Data Sekolah Kementerian Pendidikan Nasional, Republik Indonesia 2010 / 2011M...

У этого термина существуют и другие значения, см. Кайрат. Кайрат Полноеназвание Футбольный клуб «Кайрат» Прозвище Жёлто-чёрные[1] Основан 1954; 70 лет назад (1954) Стадион «Центральный» Вместимость 23 804 Владелец Кайрат Боранбаев[2][3][4] Ген. директо...

Complex of natural caves in Missouri, USA Watercolor painting by Anna Maria von Phul, A View of a Cave, 2 Miles from St. Louis, Missouri Territory, 1818 The Caves of St. Louis have been important in the economic development of St. Louis, Missouri, United States. The city was built upon a complex of natural caves which were once used for the lagering of beer by early German immigrant brewers. Caves are naturally cool, which was especially attractive to brewers before the advent of refrigeratio...

American racing driver This biography of a living person needs additional citations for verification. Please help by adding reliable sources. Contentious material about living persons that is unsourced or poorly sourced must be removed immediately from the article and its talk page, especially if potentially libelous.Find sources: Billy Roe – news · newspapers · books · scholar · JSTOR (December 2022) (Learn how and when to remove this message) Billy R...

У этого термина существуют и другие значения, см. Осьминог (значения). Осьминогиангл. Squidbillies Жанр комедия Создатели Джим ФортиэрДэйв Уиллис Рассказчик Дэйв Уиллис Композитор Билли Джо Шэйвер[вд] Страна США Язык английский Число сезонов 11 Число серий 117 (список ...

Unified combatant command of the United States Armed Forces responsible for the European region This article needs additional citations for verification. Please help improve this article by adding citations to reliable sources. Unsourced material may be challenged and removed.Find sources: United States European Command – news · newspapers · books · scholar · JSTOR (March 2023) (Learn how and when to remove this message) United States European CommandE...

American politician (1796–1866) For other people with the same name, see John Morehead (disambiguation). John Motley Morehead29th Governor of North CarolinaIn officeJanuary 1, 1841 – January 1, 1845Preceded byEdward Bishop DudleySucceeded byWilliam Alexander GrahamMember of the North Carolina General Assembly Personal detailsBorn(1796-07-04)July 4, 1796Pittsylvania County, VirginiaDiedAugust 27, 1866(1866-08-27) (aged 70)Rockbridge Springs, VirginiaNationalityAmericanPol...

Dollaro zimbabwesefuori corso Codice ISO 4217ZWL[1](ex ZWR, ZWN e ZWD) Stati Zimbabwe Simbolo$ (Z$ o ZW$) FrazioniCent (1/100) (non usata) MoneteNessuna Banconote$1, $5, $10, $20, $50, $100, $500 Entità emittenteReserve Bank of Zimbabwe Sito webwww.rbz.co.zw Periodo di circolazione18 aprile 1980 - 12 aprile 2009 Sostituita daDollaro statunitense dal 12 aprile 2009 Tasso di cambioSi veda la sezione dedicata() Il dollaro zimbabwese era utilizzato insieme al dollaro s...

1990 short story collection by Edna O'Brien Lantern Slides First edition (UK)AuthorEdna O'BrienLanguageEnglishPublisherWeidenfeld & Nicolson (UK)Farrar, Straus & Giroux (US)Publication date1990Publication placeIrelandPages215ISBN978-0-297-84019-0 Lantern Slides is a short story collection by Irish author Edna O'Brien and won the 1990 Los Angeles Times Book Prize for Fiction.[1] It contains twelve stories, published in 1990 by Weidenfeld & Nicolson in the UK and by Farrar, ...
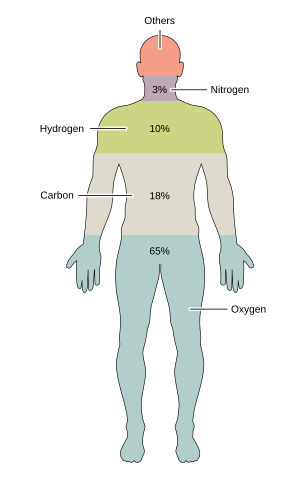
Entire structure of a human being Anatomy of the human body redirects here. For the textbook, see Gray's Anatomy. Female (left) and male (right) adult human bodies photographed in ventral (above) and dorsal (below) perspectives. Naturally-occurring pubic, body, and facial hair have been deliberately removed to show anatomy. The human body is the entire structure of a human being. It is composed of many different types of cells that together create tissues and subsequently organs and then orga...

Отто Зиффлинг Общая информация Прозвище Хольц («Древесина»)[источник не указан 2067 дней] Родился 3 августа 1912(1912-08-03)Мангейм, Германская империя Умер 20 октября 1939(1939-10-20) (27 лет)Мангейм, нацистская Германия Гражданство Веймарская республика нацистская Германия Рост 17...

![{\displaystyle R_{\phi }=T_{s}\left\{T_{\theta }\left[\bigcup _{k=1}^{N}R_{s_{k}}(\phi )\right]\right\}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/bc1856e7e586f7ee944f65f6168375a4c1e2af8e)










