Проєктивний простір
|
Read other articles:

Gulat Yunani-Romawi Gulat Yunani-Romawi merupakan gaya gulat yang dipraktikkan di seluruh dunia. Olimpiade gulat Yunani-Romawi modern pertama kali diselenggarakan pada tahun 1896 dan telah dimasukkan dalam setiap edisi Olimpiade musim panas yang diadakan sejak tahun 1904.[1] Gaya gulat ini melarang para pegulatnya untuk memegang area di bawah pinggang. Pembatasan tersebut menghasilkan penekanan pada lemparan karena pegulat tidak diperbolehkan melakukan serangan untuk menjatuhkan lawan...

Masjid Jogokariyanꦩꦱ꧀ꦗꦶꦢ꧀ꦗꦒꦏꦂꦪꦤ꧀Masjid JogokariyanAgamaAfiliasiIslamProvinsiDaerah Istimewa YogyakartaLokasiLokasiJalan Jogokaryan, Mantrijeron, YogyakartaNegaraIndonesiaArsitekturTipeMasjidDibangun olehPimpinan Ranting Muhammadiyah KarangkajenPeletakan batu pertama1966Situs webmasjidjogokariyan.com Masjid Jogokariyan (Jawa: ꦩꦱ꧀ꦗꦶꦢ꧀ꦗꦒꦏꦂꦪꦤ꧀, translit. Masjid Jagakaryan) adalah masjid di Jalan Jogokaryan, Mantrijeron, Yogyakarta, ...

artikel ini tidak memiliki pranala ke artikel lain. Tidak ada alasan yang diberikan. Bantu kami untuk mengembangkannya dengan memberikan pranala ke artikel lain secukupnya. (Pelajari cara dan kapan saatnya untuk menghapus pesan templat ini) Artikel ini sebatang kara, artinya tidak ada artikel lain yang memiliki pranala balik ke halaman ini.Bantulah menambah pranala ke artikel ini dari artikel yang berhubungan atau coba peralatan pencari pranala.Tag ini diberikan pada Februari 2023. Router pla...

Teruntum Lumnitzera racemosa, pelat botani menurut Blanco Klasifikasi ilmiah Kerajaan: Plantae (tanpa takson): Angiospermae (tanpa takson): Eudikotils (tanpa takson): Rosids Ordo: Myrtales Famili: Combretaceae Genus: LumnitzeraWilld. (1803)[1] Peta persebaran Teruntum[1] Sinonim[2] Bruguiera Thouars Funckia Dennst. Petaloma Roxb. Pokornya Montrouz. Problastes Reinw. Pyrrhanthus Jack Teruntum atau Duduk (Lumnitzera ) adalah sebuah genus tumbuhan mangrove dalam famili C...
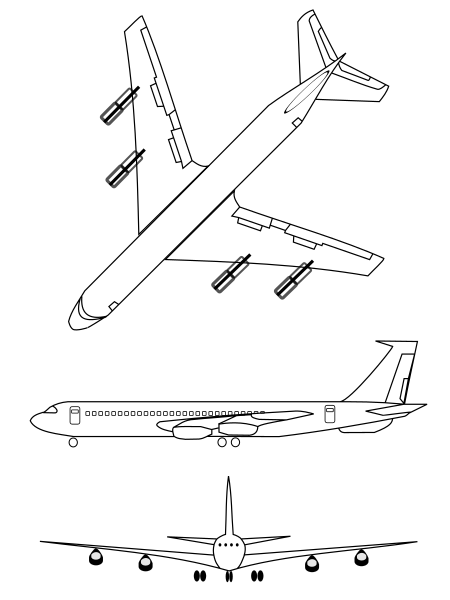
Boeing 707Un Boeing 707 in versione KC-135 della United States Air ForceDescrizioneTipoAereo di lineaAereo Cargo Equipaggio2 piloti + 1 Ingegnere di volo+gli assistenti di volo Progettista Boeing Costruttore Boeing Data primo volo20 dicembre 1957 Anni di produzione1957-1978 Data entrata in servizio26 ottobre 1958 con Pan Am Utilizzatori principali (Giugno 2023) United States Air Force467 esemplari United States Navy16 esemplari Armée de l'air15 esemplari Utilizzatori storici P...

Monarchy of the Kingdom of Sweden This article is about the Swedish monarchy as an institution. For a list of kings and queens regnant of Sweden, see List of Swedish monarchs. For a list of Swedish princes and princesses, see Swedish royal family. King of SwedenSveriges KonungGreater coat of arms of SwedenIncumbentCarl XVI Gustafsince 15 September 1973 DetailsStyleHis MajestyHeir apparentCrown Princess VictoriaFirst monarchEric the VictoriousResidenceStockholm Palace[1]Drott...

Election in Connecticut Main article: 1856 United States presidential election 1856 United States presidential election in Connecticut ← 1852 November 4, 1856 1860 → Nominee John C. Frémont James Buchanan Party Republican Democratic Home state California Pennsylvania Running mate William L. Dayton John C. Breckinridge Electoral vote 6 0 Popular vote 42,717 34,997 Percentage 53.18% 43.57% County Results Frémont 40–50% ...

Cave in Western Cape, South Africa Elands Bay CaveLocationElands Bay, Western Cape Province, South AfricaCoordinates32°19′03.5″S 18°19′04.6″E / 32.317639°S 18.317944°E / -32.317639; 18.317944 Elands Bay Cave is located near the mouth of the Verlorenvlei estuary on the Atlantic coast of South Africa's Western Cape Province.[1] The climate has continuously become drier since the habitation of hunter-gatherers in the Later Pleistocene. The archaeologic...

باسالت الإحداثيات 39°22′06″N 107°02′17″W / 39.3683°N 107.038°W / 39.3683; -107.038 [1] تقسيم إداري البلد الولايات المتحدة[2] التقسيم الأعلى مقاطعة إيغلمقاطعة بيتكين خصائص جغرافية المساحة 5.19768 كيلومتر مربع5.152786 كيلومتر مربع (1 أبريل 2010) ارتفاع 2015 متر ...

Khash Khash (bahasa Armenia: խաշ; bahasa Azerbaijan: xaş bahasa Georgia: ხაში, khashi), Kale Pache (Persia: کله پاچه; Turki: Kelle Paça), Pacha (Arab: باجة; bahasa Breton: Пача) adalah hidangan kaki sapi (dan terkadang kepala) yang dididihkan. Makanan ini adalah hidangan di Armenia, Azerbaijan, Iran, Iraq, Georgia, Bulgaria dan Turki. Pranala luar Khash web site with pictures and links Khash and other Azeri adventures

哈比卜·布尔吉巴الحبيب بورقيبة第1任突尼斯总统任期1957年7月25日—1987年11月7日(30年105天)总理巴希·拉德加姆(英语:Bahi Ladgham)(1969年-1970年)赫迪·努伊拉(英语:Hedi Nouira)(1970年-1980年)穆罕默德·姆扎利(英语:Mohammed Mzali)(1980年-1986年)拉希德·斯法尔(英语:Rachid Sfar)(1986年-1987年)宰因·阿比丁·本·阿里(1987年)继任宰因·阿比丁·本·...

هذه المقالة عن عن كلية اللغات والترجمة في جامعة الملك سعود. لمعانٍ أخرى، طالع كلية اللغات (توضيح). كلية اللغات والترجمة (جامعة الملك سعود) معلومات التأسيس 1977 الموقع الجغرافي البلد السعودية إحصاءات تعديل مصدري - تعديل كلية اللغات والترجمة بجامعة الملك سعود بدأت...

Artikel ini perlu dikembangkan agar dapat memenuhi kriteria sebagai entri Wikipedia.Bantulah untuk mengembangkan artikel ini. Jika tidak dikembangkan, artikel ini akan dihapus. State of AmapáState BenderaLambang kebesaranLocation of State of Amapá in BrazilCountry BrazilCapital and Largest CityMacapáPemerintahan • GovernorCamilo Góes Capiberibe • Vice GovernorDora Nascimento de SouzaLuas • Total142.814,585 km2 (55,141,020 sq mi)Perin...

BaseAlbum mini karya JonghyunDirilis12 Januari 2015 (2015-01-12)Genre K-pop Dance R&B / Soul Durasi28:22Bahasa Korea Inggris Label S.M. Entertainment KT Music ProduserLee Soo-man (executive)Kronologi Jonghyun Base(2015) The Collection: Story Op.1(2015)String Module Error: Match not found2015 Singel dalam album Base Déjà-BooDirilis: 7 Januari 2015 Crazy (Guilty Pleasure)Dirilis: 12 Januari 2015 Video musikDéjà-Boo di YouTubeCrazy (Guilty Pleasure) di YouTube Base adalah album ...

France 3 MéditerranéeDiluncurkan20 September 1954PemilikFrance TélévisionsSloganDe près, on se comprend mieuxNegara PerancisKantor pusatMarseilleSitus webméditerranée.france3.fr France 3 Méditerranée merupakan satu dari 13 stasiun regional France 3, mengudara di region Côte d'Azur dari kantornya di Marseilles. Menyiarkan berita regional, program dan olahraga. Sejarah RTF Télé-Marseille mulai mengudara 20 September 1954. Tahun 1964, RTF digantikan dengan ORTF oleh peemrintah, ...

This article needs additional citations for verification. Please help improve this article by adding citations to reliable sources. Unsourced material may be challenged and removed.Find sources: 25 Years – The Chain – news · newspapers · books · scholar · JSTOR (May 2021) (Learn how and when to remove this message) 1992 box set by Fleetwood Mac25 Years – The ChainBox set by Fleetwood MacReleased24 November 1992 (1992-11-24)Re...

Governors of the state of Tripura, India Governor of TripuraRaj Bhavan AgartalaIncumbentNallu Indrasena Reddysince 26 October 2023StyleHis ExcellencyResidenceRaj Bhavan; AgartalaAppointerPresident of IndiaTerm length5 YearsFormationrajbhavan.tripura.gov.in The state of Tripura is surrounded by eastern Bangladesh. This is a list of the governors of Tripura, a state in northeast India, since its inception as a state on 21 January 1972.[1] Powers and functions See also: Powers and f...

American politician For his son, the senator, governor, and judge, see Ernest W. Gibson Jr. For his grandson, the judge, see Ernest W. Gibson III. Ernest W. GibsonUnited States Senatorfrom VermontIn officeNovember 21, 1933 – June 20, 1940Preceded byPorter H. DaleSucceeded byErnest W. Gibson Jr.Member of the U.S. House of Representativesfrom VermontIn officeNovember 6, 1923 – October 19, 1933Preceded byPorter H. DaleSucceeded byCharles A. PlumleyConstituency2n...

American politician Gregory S. LucasMember of the Pennsylvania House of Representativesfrom the 5th districtIn office2013 – January 6, 2015Preceded byJohn R. EvansSucceeded byBarry Jozwiak Personal detailsBorn (1960-09-15) September 15, 1960 (age 63)Edinboro, Pennsylvania, U.S.Political partyRepublicanSpouseRose E. LucasResidence(s)Edinboro, Pennsylvania, U.S.Alma materCalifornia University of PennsylvaniaOccupationTeacher Gregory S. Lucas (born September 15, 1960)...
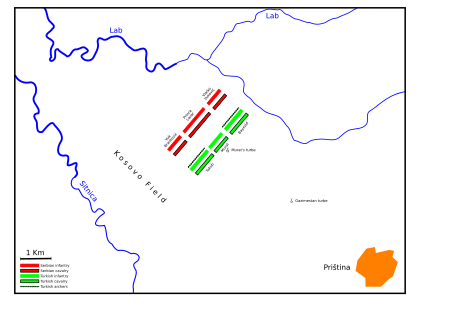
1389 battle between Christian coalition led by Moravian Serbia and the Ottoman Empire This article is about the battle in 1389. For other battles, see Battle of Kosovo (disambiguation). Battle of KosovoPart of the Ottoman wars in Europe and the Serbian-Ottoman WarsBattle of Kosovo, by Adam Stefanović (1870)Date15 June[A] 1389LocationKosovo field, District of Branković42°43′03″N 21°05′06″E / 42.71750°N 21.08500°E / 42.71750; 21.08500Result Inconclusive[...



















![{\displaystyle (x_{1},x_{2},...,x_{n})\mapsto [x_{1},x_{2},...,x_{n},1]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/b33e745bee8a70ddf86d036b8e3436786f52895d)
![{\displaystyle [y_{1},y_{2},\ldots ,y_{n},0]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/d23173613c9ecdf1ab4fe3adc22e2643ba5aecb9)




![{\displaystyle [-b,a,0]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/5b28440a5ef0cd517d60380a5ec7430fa1d356ca)




![{\displaystyle P[X_{1},X_{2},...,X_{n},X_{n+1}]=X_{n+1}^{d}p\left({\frac {X_{1}}{X_{n+1}}},{\frac {X_{2}}{X_{n+1}}},...,{\frac {X_{n}}{X_{n+1}}}\right)}](https://wikimedia.org/api/rest_v1/media/math/render/svg/5818005450d51fb7578fce2c389507cfbc609b94)





![{\displaystyle [x_{0},y_{0},1]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/230df02b07f51f818f8917cd2dfaf15925138003)
![{\displaystyle [-b_{1},a_{1},0]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/05d047c83232641aecde047b9b7ea9d5be607978)
![{\displaystyle [-b_{2},a_{2},0]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/11079a9da9f2c9fe387d175088afca91558eb5da)












