Правило Гюккеля

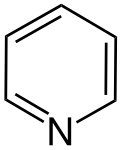
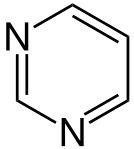
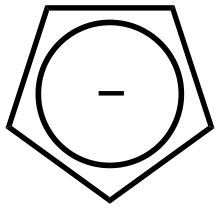
Правило Гюккеля
Названо на честь Еріх Хюккель Редагувати інформацію у Вікіданих

Правило Гюккеля (англ. Hückel's rule) — спосіб оцінки наявності ароматичних властивостей у циклічних органічних молекулах із циклічно кон'югованими π-зв'язками. Квантово-механічну основу для цього правила розробив німецький хімік Еріх Гюккель у 1931 році (див. метод Гюккеля)[1][2].

Правило

Моноциклічна плоска (або майже плоска) сполука, що має циклічно кон'югованих π-електронів (n = 0, 1, 2,..), має високу стабільність і називається ароматичною[3]. Відповідно, плоска молекула з циклічно кон'югованими π-електронів є нестабільною й називається антиароматичною.

Теоретично, n може дорівнювати нулю або будь-якому цілому числу більше нуля, але практичні приклади відомі лише для значень n = 0 до приблизно n = 6[4].

Ілюстрацією правила Гюккеля є цикл Фроста.

Приклади

Анулени

Класичними сполуками, на прикладі яких демонструється правило Гюккеля, є анулени. Нижче представлені приклади ануленів та їх відповідність до правила Гюккеля (n = 1 — 4)[5]:

Найважливішим прикладом ароматичної сполуки є бензен, який має 6 π-електронів (n = 1).

Гетероароматичні сполуки

Гетероциклічні сполуки, що відповідають правилу Гюккеля, теж мають певні ароматичні властивості. При цьому слід поділяти між п'ятичленними й шестичленними гетероароматами. У випадку п'ятичленних гетероароматів (напр., пірол, фуран, тіофен) делокалізація π-електронів реалізується за участі орбіталі гетероатома з вільною електронною парою; ця електронна пара також бере участь в делокалізації, тому також рахується згідно з правилом . У шестичленних гетероароматах (піридин, піримідин) гетероатом (у нейтральних гетероароматах це, зазвичай, Нітроген) утворює три зв'язки з атомами циклу, а його вільна електронна пара не бере участь у делокалізації.

Заряджені молекули

Ароматичні або антиароматичні властивості можуть проявляти не лише нейтральні молекули, але й іони циклічних полієнів; при цьому циклічна делокалізація реалізується за рахунок пустих p-орбіталей (у випадку карбокатіону) або p-орбіталей з вільною електронною парою (у випадку карбаніону). Тобто, вільні електронні пари також беруть участь в делокалізації, тому рахуються разом з π-електронами. Вільні p-орбіталі в карбокатіонах, таким чином, надають 0 електронів до делокалізації.

Найпростішим ароматичним іоном є циклопропеніл-катіон, що містить 2 π-електрони (n = 0):

катіон Trichlorcyclopropenyl

Наступним у цьому списку йде циклопентадієніл-аніон (Cp-) (Cyclopentadienyl_anion[en]), що має 6 делокалізованих π-електронів. Тропілій-катіон, до речі, теж має 6 π-електронів, але є семичленним циклом. Наступним ароматичним іоном є циклооктатетраєнід-діаніон (en1[en], en2), що має 10 π-електронів:

  • Циклопентадієніл-аніон
    Циклопентадієніл-аніон
  • Тропілій-катіон
    Тропілій-катіон
  • Циклооктатетраєніл-діаніон
    Циклооктатетраєніл-діаніон
Пірилій-іон

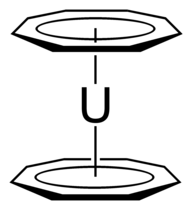
Також відомі випадки гетероароматичних іонів, наприклад пірилій-катіон.

Звісно, ароматичні іони, хоч і вважаються ароматичними, є доволі реактивними, хоча тропілій-катіон можна кристалізувати разом із деякими аніонами (наприклад, бромід, йодид, перхлорат, тетрафлуороборат)[6][7][8]. Тим не менш, звичною сферою застосування ароматичних іонів є металоорганічна хімія, де ці іони використовуються в якості лігандів у металоценах:

Обмеження й недоліки методу

Правило Гюкеля добре працює для моноциклічних сполук[9], але є неточним у випадку конденсованих поліциклічних ароматів. Наприклад, нафталін та антрацен мають 10 та 14 π-електронів, а от ароматичні пірен (16 π-електронів) і коронен (24 π-електрони) вже не відповідають вимозі «». Альтернативно можна рахувати тільки ті електрони, що є моноциклічно кон'югованими (наприклад, тільки зовнішнє «кільце» коронену, яке має 18 π-електронів), але такий підхід можливий не в усіх випадках.

Однак, підхід «лічити тільки моноциклічно кон'юговані π-електрони» є дещо виправданим, що підтверджено теоретичними розрахунками[10].

  • Моноциклічна делокалізація π-електронів у коронені спостерігається поміж зв'язків, що помічені червоним
    Моноциклічна делокалізація π-електронів у коронені спостерігається поміж зв'язків, що помічені червоним
  • Моноциклічна делокалізація π-електронів у порфіні спостерігається поміж зв'язків, що помічені червоним.
    Моноциклічна делокалізація π-електронів у порфіні спостерігається поміж зв'язків, що помічені червоним.

Див. також

Примітки

  1. ↑ Hückel, Erich (1931-03). Quantentheoretische Beiträge zum Benzolproblem: I. Die Elektronenkonfiguration des Benzols und verwandter Verbindungen. Zeitschrift für Physik (нім.). Т. 70, № 3-4. с. 204—286. doi:10.1007/BF01339530. ISSN 1434-6001. Процитовано 21 вересня 2024.
  2. ↑ Hückel, Erich (1938). Grundzüge der Theorie ungesättiger und aromatischer Verbindungen. Berlin: Verlag Chem. с. 77—85.
  3. ↑ A. D. McNaught A. Wilkinson (1997). IUPAC. Compendium of Chemical Terminology, 2nd ed. (the "Gold Book") (англ.). Oxford: Blackwell Scientific Publications. doi:10.1351/goldbook. ISBN 0-9678550-9-8. {{cite book}}: символ зміни рядка в |last= на позиції 15 (довідка)
  4. ↑ March, Jerry (1985). Advanced Organic Chemistry: Reactions, Mechanisms, and Structure (3rd ed.) (англ.). New York: Wiley. ISBN 0-471-85472-7.
  5. ↑ Vollhardt, K. Peter C. (2003). Organic chemistry : structure and function (вид. 4th ed.). New York: W.H. Freeman and Co. ISBN 0-7167-4374-4. OCLC 49902193.
  6. ↑ Von E.Doering, W.; Knox, L. H. (1954-06). The Cycloheptatrienylium (Tropylium) Ion. Journal of the American Chemical Society (англ.). Т. 76, № 12. с. 3203—3206. doi:10.1021/ja01641a027. ISSN 0002-7863.
  7. ↑ Balaban, Alexandru T.; Oniciu, Daniela C.; Katritzky, Alan R. (2004-05). Aromaticity as a Cornerstone of Heterocyclic Chemistry. Chemical Reviews (англ.). Т. 104, № 5. с. 2777—2812. doi:10.1021/cr0306790. ISSN 0009-2665.
  8. ↑ Kitaigorodskii, A. I.; Struchkov, Yu. T.; Khotsyanova, T. L.; Vol'pin, M. E.; Kursanov, D. N. (1960-01). Crystal structures of tropylium perchlorate and iodide. Bulletin of the Academy of Sciences of the USSR Division of Chemical Science (англ.). Т. 9, № 1. с. 32—36. doi:10.1007/BF01178699. ISSN 0568-5230.
  9. ↑ Roberts, John D.; Streitwieser, Andrew, Jr.; Regan, Clare M. (1952). Small-Ring Compounds. X. Molecular Orbital Calculations of Properties of Some Small-Ring Hydrocarbons and Free Radicals. J. Am. Chem. Soc. 74 (18): 4579—82. doi:10.1021/ja01138a038.
  10. ↑ Geuenich, Daniel; Hess, Kirsten; Köhler, Felix; Herges, Rainer (2005-10). Anisotropy of the Induced Current Density (ACID), a General Method To Quantify and Visualize Electronic Delocalization. Chemical Reviews. Т. 105, № 10. с. 3758—3772. doi:10.1021/cr0300901. ISSN 0009-2665.

Information related to Правило Гюккеля