Read other articles:

Basilika Maria, Bunda Belas KasihBasilika Minor Maria, Bunda Belas Kasihbahasa Slovenia: Bazilika Matere UsmiljenjaBasilika Maria, Bunda Belas KasihLokasiMariborNegara SloveniaDenominasiGereja Katolik RomaArsitekturStatusBasilika minorStatus fungsionalAktif Basilika Maria, Bunda Belas Kasih (bahasa Slovenia: Bazilika Matere Usmiljenja) adalah sebuah gereja basilika minor Katolik yang terletak di Maribor, Slovenia. Basilika ini ditetapkan statusnya pada 1906 dan didedikasikan kepa...

Nicolas de LargillièreLukisan diri Nicolas de Largillierre.Lahir(1656-10-10)10 Oktober 1656Paris, PrancisMeninggal20 Maret 1746(1746-03-20) (umur 89)Paris, PrancisKebangsaanPrancisPendidikanAntwerpDikenal atasPelukisGerakan politikRococo Nicolas de Largillière (10 Oktober 1656 – 20 Maret 1746) adalah seorang pelukis yang lahir di Paris, Prancis. Biografi Kehidupan awal Ayah Largillière, seorang pedagang, membawanya ke Antwerp pada usia tiga tahun. Sebagai seorang anak laki-laki, ia...

Gereja di Vinnytsia Eparki Vinnytsia adalah sebuah eparki Gereja Ortodoks Ukraina yang terletak di Vinnytsia, Ukraina. Eparki tersebut didirikan pada tahun 2018.[1] Referensi ^ https://www.ukrinform.ua/rubric-regions/2602519-u-vinnici-parafiani-svatopreobrazenskogo-soboru-perejsli-do-upc.html

مدرسة الشرطة بسطيف الدولة  الجزائر الولاء المديرية العامة للأمن الوطني الدور تكوين الحجم حوالي 500 طالب متربص جزء من شرطة المقر الرئيسي مدرسة الشرطة القادة القائد الحالي مدير المدرسة تعديل مصدري - تعديل   مدرسة الشرطة بسطيف هي أحد مراكز تكوين الشرطة الجزائرية، تم إنشا...

Untuk orang yang membuat kartun animasi, lihat animator. KartunisKartunis Jack Elrod sedang mengerjakan halaman Minggu dari komik strip Mark TrailKomik Balon ucapan Studi komik Pendidikan Sejarah Glosarium Metode Kartun Fumetti Format Media Buku komik Strip komik Kartun editorial Kartun lelucon Novel grafik Komik web Webtoon Komik menurut Negara dan Budaya Komik Amerika Komik Belanda Komik Belgia Komik Britania Raya Komik Indonesia Komik Italia Komik Jerman Komik Kanada Komik Prancis-Belgia M...

  此條目介紹的是拉丁字母中的第2个字母。关于其他用法，请见「B (消歧义)」。   提示：此条目页的主题不是希腊字母Β、西里尔字母В、Б、Ъ、Ь或德语字母ẞ、ß。 BB b(见下)用法書寫系統拉丁字母英文字母ISO基本拉丁字母（英语：ISO basic Latin alphabet）类型全音素文字相关所属語言拉丁语读音方法 [b][p][ɓ](适应变体)Unicode编码U+0042, U+0062字母顺位2数值 2歷史發...

French politician Odilon BarrotPrime Minister of FranceIn office20 December 1848 – 31 October 1849Preceded byLouis-Eugène CavaignacSucceeded byAlphonse Henri, comte d'Hautpoul Personal detailsBorn19 July 1791VillefortDied6 August 1873(1873-08-06) (aged 82)BougivalPolitical partyDoctrinaires (1815–1830)Party of Movement (1830–1848)Party of Order (1848–1852) Camille Hyacinthe Odilon Barrot (French pronunciation: [ɔdilɔ̃ baʁo]; 19 July 1791 – 6 August 1873) w...

Vijaya DasaTemple in honor of Vijaya DasaPersonalBornDasa1682 CECheekalaparvi (Present day Manvi taluk, Raichur district, Karnataka)Died1755 CEPresent day Karnataka, IndiaReligionHinduismOccupationSaint, Poet, philosopher, composer Part of a series onDvaita Saints Madhvacharya Padmanabha Tirtha Narahari Tirtha Akshobhya Tirtha Jayatirtha Sripadaraja Vyasatirtha Vadiraja Tirtha Raghuttama Tirtha Vijayendra Tirtha Sudhindra Tirtha Satyanatha Tirtha Raghavendra Tirtha Sumatindra Tirtha Haridasa...

Wakil Bupati ManokwariPetahanaDrs. Edi Budoyosejak 26 Februari 2021Masa jabatan5 tahunDibentuk2000Pejabat pertamaIr. Dominggus Buiney, M.M.Situs webwww.manokwarikab.go.id Berikut ini adalah daftar Wakil Bupati Manokwari dari masa ke masa. No Wakil Bupati Mulai Jabatan Akhir Jabatan Prd. Ket. Bupati 1 Ir.Dominggus BuineyM.M. 2000 2005 1   Drs.Dominggus Mandacan 2005 2010 2   Jabatan kosong 2010 2011 -   Drs.Anthon LesnussaM.M.(Pelaksana Harian) 2 Dr.Robert K. R. HammarS.H.,...

Football clubDalhousieThe earliest crest of Dalhousie ACFull nameDalhousie Athletic ClubShort nameDACFounded1878; 146 years ago (1878) (as Trades Club)[1]1880; 144 years ago (1880) (as Dalhousie Club)GroundVariousHead coachMridul BanerjeeLeagueCalcutta Premier Division Home colours Away colours Dalhousie Athletic Club is an Indian professional sports club based in Kolkata, West Bengal, best known for its football section.[2][3][...

DctP component of Tripartite ATP-independent periplasmic transporterIdentifiersSymbolDctPPfamPF03480Pfam clanCL0177InterProIPR018389TCDB2.A.56Available protein structures:Pfam  structures / ECOD  PDBRCSB PDB; PDBe; PDBjPDBsumstructure summary DctQ component of Tripartite ATP-independent periplasmic transporterIdentifiersSymbolDctQPfamPF04290InterProIPR007387TCDB2.A.56Available protein structures:Pfam  structures / ECOD  PDBRCSB PDB; PDBe; PDBjPDBsumstructure summaryDctM-li...

University in Qatar Carnegie Mellon University QatarFront entrance at sunsetOther nameCMU-QMottoMy heart is in the work (Andrew Carnegie)TypePrivate satellite campusEstablished2004; 20 years ago (2004)Parent institutionCarnegie Mellon UniversityPresidentFarnam JahanianProvostJames GarrettDeanMichael TrickAcademic staff64Administrative staff90Undergraduates467 (Fall 2022)[1]LocationDoha, Qatar25°18′59″N 51°26′20″E / 25.31639°N 51.43889°E&#x...

艾哈迈德·塞古·杜尔总统杜尔、代表几内亚共和国在美国马里兰访问华盛顿特区期间抵达安德鲁斯空军基地。 (1982年6月) 第一任几内亚总统任期1958年10月2日—1984年3月26日前任无，职务设立继任路易斯·兰萨纳·贝阿沃吉 个人资料出生(1922-01-09)1922年1月9日 法兰西第三共和国法属西非法拉纳逝世1984年3月26日(1984歲—03—26)（62歲） 美國克利夫兰, 俄亥俄州墓地科奈克里大清�...

海尔·塞拉西一世埃塞俄比亚皇帝統治1930年11月2日－1974年9月12日（43年314天）加冕1930年11月2日前任佐迪图繼任阿姆哈·塞拉西一世（流亡）埃塞俄比亞攝政王統治1916年9月27日－1930年11月2日（14年36天）出生(1892-07-23)1892年7月23日 埃塞俄比亚帝国哈勒爾州逝世1975年8月27日(1975歲—08—27)（83歲） 衣索比亞亚的斯亚贝巴安葬2000年11月5日圣三一大教堂配偶梅南·阿斯福（1889年－1962�...

Ilustrasi lepus cornutus (kelinci bertanduk) dari Tableau Encyclopedique et Methodique (1789), yang diduga terjangkit virus Papiloma shope, dan dianggap sebagai inspirasi mitos Jackalope. Jackalope adalah makhluk mitos dalam budaya rakyat Amerika Utara yang diwujudkan sebagai seekor kelinci (jackrabbit) yang bertanduk antelop atau rusa, dan adakalanya berekor dan bertungkai belakang seperti burung pegar. Ada kemungkinan bahwa legenda jackalope diilhami oleh penampakan kelinci yang dijangkiti ...

Main article: Cricket at the Asian Games This is the complete list of Asian Games medalists in cricket from 2010 to 2022.[1] Men Games Gold Silver Bronze 2010 Guangzhou  Bangladesh (BAN)Mohammad AshrafulShamsur RahmanNaeem IslamFaisal HossainShahadat HossainMahbubul AlamMohammad Nazmul HossainNazimuddinSuhrawadi ShuvoDolar MahmudMohammad MithunNasir HossainRony TalukdarShuvagata HomSabbir Rahman  Afghanistan (AFG)Gulbadin NaibMohammad ShahzadSami AghaMohammad Nabi...

German art historian (born 1965) This article is an autobiography or has been extensively edited by the subject or by someone connected to the subject. It may need editing to conform to Wikipedia's neutral point of view policy. There may be relevant discussion on the talk page. (January 2024) (Learn how and when to remove this message) Grau in transmediale 2010. Oliver Grau (born 24 October 1965) is a German art historian and media theoretician with a focus on image science, modernity and med...

El Salvador16º lugar Oficial Alternativo Asociación Federación Salvadoreña de Fútbol Confederación Concacaf Participación 1 Entrenador Hernán Carrasco La Selección de El Salvador fue uno de los 16 equipos participantes de la Copa Mundial de Fútbol de 1970 realizada en México. Se clasificó sorteando las diversas rondas de clasificación de la CONCACAF junto con otros 13 equipos de la zona. Uno de estos partidos ante Honduras se jugó bajo un clima de tensión y hostilidad a raíz ...

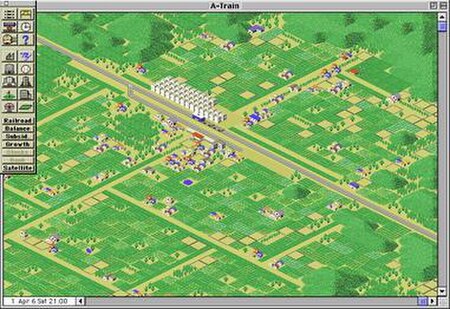
Video game series For other uses, see A-Train (disambiguation). Video game seriesA-TrainEuropean cover art of A-Train 6Genre(s)Business simulationDeveloper(s)ArtdinkPublisher(s)JP: ArtdinkNA: MaxisEU: Ocean SoftwareEU: Midas Interactive EntertainmentPlatform(s) Various FM-7, PC-88, PC-98, Sharp X1, Sharp MZ, Famicom, MSX2, X68000, Amiga, FM Towns, Mac, Mega Drive, Nintendo DS, 3DS, Switch, PC Engine, PlayStation, PlayStation 2, PlayStation Portable, Super Famicom, Wii, Windows, Xbox 360 First...

Untuk kegunaan lain, lihat Dia (disambiguasi). DiaGenre Drama Roman PembuatMD EntertainmentDitulis olehZara ZettiraSutradaraEncep MasdukiPemeran Lulu Tobing Ari Wibowo Teuku Ryan Dwi Yan Nena Rosier Elsye Virgita Shenny Andrea Debby Cynthia Dewi Penggubah lagu tema Dian Pramana Poetra Alena Rio Febrian Lagu pembuka Masih Ada — Warna [a] Selembar Cinta — Alena [b] Ku Ada Disini — Rio Febrian [c] Lagu penutup Masih Ada — Warna [d] Selembar Cinta — Alena...