Людвіг Мюллер
| |||||||||||||||||||||||||
Read other articles:

Peta Lokasi Kabupaten Murung Raya di Kalimantan Tengah Berikut adalah daftar kecamatan dan kelurahan di Kabupaten Murung Raya, Provinsi Kalimantan Tengah, Indonesia. Kabupaten Murung Raya terdiri dari 10 kecamatan, 9 kelurahan, dan 116 desa. Pada tahun 2017, jumlah penduduknya mencapai 105.454 jiwa dengan luas wilayah 23.700,00 km² dan sebaran penduduk 5 jiwa/km².[1][2] Daftar kecamatan dan kelurahan di Kabupaten Murung Raya, adalah sebagai berikut: Kode Kemendagri Kecamatan...

Protein-coding gene in the species Homo sapiens CLIC1Available structuresPDBOrtholog search: PDBe RCSB List of PDB id codes1K0M, 1K0N, 1K0O, 1RK4, 3O3T, 3P8W, 3P90, 3QR6, 3SWL, 3TGZ, 3UVH, 4IQA, 4JZQ, 4K0G, 4K0NIdentifiersAliasesCLIC1, G6, NCC27, chloride intracellular channel 1, CL1C1, CLCNL1External IDsOMIM: 602872 MGI: 2148924 HomoloGene: 20343 GeneCards: CLIC1 Gene location (Human)Chr.Chromosome 6 (human)[1]Band6p21.33Start31,730,581 bp[1]End31,739,763 bp[1]Gene lo...

1918 film True BlueDirected byFrank LloydWritten byFrank LloydProduced byWilliam FoxStarringWilliam FarnumKathryn AdamsCharles ClaryCinematographyWilliam C. FosterProductioncompanyFox FilmDistributed byFox FilmRelease dateMay 5, 1918Running time60 minutesCountryUnited StatesLanguagesSilentEnglish intertitles True Blue is a 1918 American silent Western film directed by Frank Lloyd and starring William Farnum, Kathryn Adams and Charles Clary.[1] Cast William Farnum as Bob McKeever Kathr...

Mayor of Philadelphia from 2016 to 2024 Jim Kenney99th Mayor of PhiladelphiaIn officeJanuary 4, 2016 – January 1, 2024Preceded byMichael NutterSucceeded byCherelle ParkerMember of the Philadelphia City Councilfrom the at-large districtIn officeJanuary 6, 1992 – January 29, 2015Preceded byGeorge Burrell Personal detailsBornJames Francis Kenney (1958-08-07) August 7, 1958 (age 65)Philadelphia, Pennsylvania, U.S.Political partyDemocraticEducationLa Salle University (BA...

Clifford Glenwood Shull (23 September 1915 – 31 Maret 2001) adalah seorang fisikawan Amerika Serikat pemenang Penghargaan Nobel. Ia menerima Penghargaan Nobel dalam Fisika 1994 dengan orang Kanada Bertram Neville Brockhouse untuk pengembangan teknik penghamburan elektron, khususnya teknik difraksi neutron, untuk mempelajari bahan kental. Trivia Hadiah Nobel yang dimenangkan Clifford Shull (diterima dengan Bertram N. Brockhouse) pada tahun 1994 dianugerahkan lama setelah karya ...

1984 film directed by Miloš Forman AmadeusTheatrical release poster by Peter SísDirected byMiloš FormanScreenplay byPeter ShafferBased on Amadeusby Peter Shaffer Mozart and Salieriby Alexander Pushkin Produced bySaul ZaentzStarring F. Murray Abraham Tom Hulce Elizabeth Berridge Simon Callow Roy Dotrice Christine Ebersole Jeffrey Jones Charles Kay CinematographyMiroslav OndříčekEdited by Nena Danevic Michael Chandler ProductioncompanyThe Saul Zaentz CompanyDistributed by Orion Pictures (...

Kolkata Municipal Corporation in West Bengal, IndiaWard No. 59Kolkata Municipal CorporationInteractive Map Outlining Ward No. 59Ward No. 59Location in KolkataCoordinates (dms): 22°32′43″N 88°22′38″E / 22.545333°N 88.377125°E / 22.545333; 88.377125Country IndiaStateWest BengalCityKolkataNeighbourhoodsBeniapukur, Gobra, Tangra (Seal Lane)ReservationWomen(Open)Parliamentary constituencyKolkata UttarAssembly constituencyEntallyBorough7Population ...

Le informazioni riportate non sono consigli medici e potrebbero non essere accurate. I contenuti hanno solo fine illustrativo e non sostituiscono il parere medico: leggi le avvertenze. Trombosi venosa profondaTrombosi venosa profonda alla gamba destra con rossore ed edema diffusoSpecialitàcardiologia Classificazione e risorse esterne (EN)ICD-9-CM453.40 ICD-10I80.2 MedlinePlus000156 eMedicine1911303 Modifica dati su Wikidata · Manuale La trombosi venosa profonda (TVP) è una flebotromb...

この項目には、一部のコンピュータや閲覧ソフトで表示できない文字が含まれています(詳細)。 数字の大字(だいじ)は、漢数字の一種。通常用いる単純な字形の漢数字(小字)の代わりに同じ音の別の漢字を用いるものである。 概要 壱万円日本銀行券(「壱」が大字) 弐千円日本銀行券(「弐」が大字) 漢数字には「一」「二」「三」と続く小字と、「壱」「�...

Si ce bandeau n'est plus pertinent, retirez-le. Cliquez ici pour en savoir plus. Cet article ne cite pas suffisamment ses sources (mai 2017). Si vous disposez d'ouvrages ou d'articles de référence ou si vous connaissez des sites web de qualité traitant du thème abordé ici, merci de compléter l'article en donnant les références utiles à sa vérifiabilité et en les liant à la section « Notes et références ». En pratique : Quelles sources sont attendues ? Comme...

土库曼斯坦总统土库曼斯坦国徽土库曼斯坦总统旗現任谢尔达尔·别尔德穆哈梅多夫自2022年3月19日官邸阿什哈巴德总统府(Oguzkhan Presidential Palace)機關所在地阿什哈巴德任命者直接选举任期7年,可连选连任首任萨帕尔穆拉特·尼亚佐夫设立1991年10月27日 土库曼斯坦土库曼斯坦政府与政治 国家政府 土库曼斯坦宪法 国旗 国徽 国歌 立法機關(英语:National Council of Turkmenistan) ...

Chinese politician In this Chinese name, the family name is Hu. Hu Hanmin胡漢民Chairman of KuomintangIn office7 December 1935 – 12 May 1936Preceded byWu Zhihui, Li ShizengSucceeded byChiang Kai-shekPresident of the Legislative YuanIn office8 October 1928 – 2 March 1931Preceded byOffice establishedSucceeded byLin Sen Personal detailsBorn9 December 1879Panyu, Guangdong, ChinaDied12 May 1936(1936-05-12) (aged 56)Guangdong, Republic of ChinaCause of deathIn...

Prominent lunar impact crater Feature on the moonTychoTycho seen by Lunar Reconnaissance Orbiter (rotate display if you see a crater illusion due to the atypical position of the light source). NASACoordinates43°19′S 11°22′W / 43.31°S 11.36°W / -43.31; -11.36Diameter85 km (53.4 miles)Depth4.7 km (2.9 mi)[1]Colongitude12° at sunriseEponymTycho Brahe Location of Tycho as seen from the Northern Hemisphere 3D model of Tycho crater Tycho ...

Benedictus Gotthelf Teubner. 1911 reproduction of an 1811 portrait. Grave sign of the family of B. G. Teubner Benedictus Gotthelf Teubner (born 16 June 1784 in Grosskrausnik in Luckau in Lower Lusatia; died 21 January 1856 in Leipzig) was a German bookseller and the founder of a publishing company. Life Teubner was a printer. In 1811 he brought the Weinedelsche printing press to Leipzig, which he would bring to importance within Germany. He founded another press in Dresden towards the end of ...

Lockheed Martin Corporation Тип Публичная компания Листинг на бирже NYSE: LMT Основание 1995; 29 лет назад (1995) Предшественник Lockheed и Martin Marietta Расположение США: Бетесда (Мэриленд) Ключевые фигуры Джеймс Д. Тайклет (председатель совета директоров и CEO)[1] Отрасль Аэрокосмичес...

Person who is not a member of the military For other uses, see Civilian (disambiguation). A civilian is a person who is not a member of an armed force nor a person engaged in hostilities.[1] It is slightly different from a non-combatant, because some non-combatants are not civilians (for example, military chaplains, or military personnel who are serving with a neutral country). Civilians in the territories of a party to an armed conflict are entitled to certain privileges under the cu...

Drapeau olympique de Taïwan. Taipei chinois (chinois traditionnel : 中華臺北 ; chinois simplifié : 中华台北 ; pinyin : Zhōnghuá Táiběi ou chinois simplifié : 中国台北 ; chinois traditionnel : 中國臺北 ; pinyin : Zhōngguó Táiběi ; anglais : Chinese Taipei ; français : « Taïpei chinois », « Taipei chinois », « Taïpei de Chine » ou « Taipei...

令制国一覧 > 東海道 > 武蔵国 > 久良岐郡 日本 > 関東地方 > 神奈川県 > 久良岐郡 神奈川県久良岐郡の範囲(水色:後に他郡から編入した区域) 久良岐郡(くらきぐん)は、神奈川県(武蔵国)にあった郡。現在は、中村川と堀割川の分岐点の久良岐橋、久良岐公園、横浜市能楽堂(久良岐能舞台)にその名をとどめる。 郡域 1878年(�...

Species of amphibian known for strong toxicity Rough-skinned newt Conservation status Least Concern (IUCN 3.1)[1] Scientific classification Domain: Eukaryota Kingdom: Animalia Phylum: Chordata Class: Amphibia Order: Urodela Family: Salamandridae Genus: Taricha Species: T. granulosa Binomial name Taricha granulosa(Skilton, 1849) Rough-skinned newt on the west side of the Oregon Coast Range. The rough-skinned newt or roughskin newt (Taricha granulosa) is a North American newt...
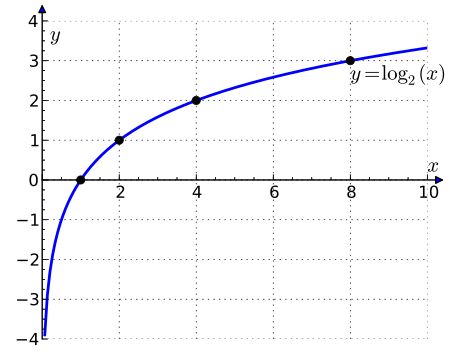
Exponent of a power of two Graph of log2 x as a function of a positive real number x In mathematics, the binary logarithm (log2 n) is the power to which the number 2 must be raised to obtain the value n. That is, for any real number x, x = log 2 n ⟺ 2 x = n . {\displaystyle x=\log _{2}n\quad \Longleftrightarrow \quad 2^{x}=n.} For example, the binary logarithm of 1 is 0, the binary logarithm of 2 is 1, the binary logarithm of 4 is 2, and the binary logari...













