Конформна група
|
Read other articles:

Virginia state legislature district District map from the 2023 election Virginia's 29th House of Delegates district elects one of 100 seats in the Virginia House of Delegates, the lower house of the state's bicameral legislature. District 29 represents the city of Winchester as well as parts of Frederick and Warren counties. The seat is currently held by Bill Wiley, who was elected in a November 3, 2020 special election. District officeholders Years Delegate Party Electoral history January 12...

American politician This article is about the Florida politician. For the former mayor of Charlotte, North Carolina, see Patrick Cannon. Pat CannonMember of the U.S. House of Representativesfrom Florida's 4th districtIn office1939–1947Preceded byJ. Mark WilcoxSucceeded byGeorge Smathers Personal detailsPolitical partyDemocratic Arthur Patrick Cannon (May 22, 1904 – January 23, 1966) was a four-term United States Representative from Florida, serving from 1939 to 1947. Early lif...

Classification of the human species Homo (humans)Temporal range: Piacenzian-Present, 2.865–0 Ma PreꞒ Ꞓ O S D C P T J K Pg N ↓ Scientific classification Domain: Eukaryota Kingdom: Animalia Phylum: Chordata Class: Mammalia Order: Primates Suborder: Haplorhini Infraorder: Simiiformes Family: Hominidae Subfamily: Homininae Tribe: Hominini Genus: HomoLinnaeus, 1758 Type species Homo sapiensLinnaeus, 1758 Species Homo sapiens Homo sapiens sapiens †Homo antecessor †Homo erectus ...

American/Canadian/French animated children's television series The Busy World of Richard ScarryCover for The Busy World of Richard Scarry: Every Day There's Something New DVDGenreAnimated seriesWritten byVariousDirected by Greg Bailey Marcos Da Silva Pascal Morelli Stephan Martinière Nadja Cozic Voices of Keith Knight Sonja Ball Theme music composerMilan KymlickaComposerLaurent PetitgirardCountry of origin Canada France No. of seasons5No. of episodes65 (195 segments)ProductionExecutive produ...

Eccellenza LombardiaSport Calcio TipoClub OrganizzatoreFIGC - Comitato Regionale Lombardia TitoloPromozione in Serie D dei vincitori di gironi e play-off nazionali Aperturasettembre Chiusuramaggio Partecipanti54 squadre FormulaTre gironi all'italiana con play-off e play-out Promozione inSerie D Retrocessione inPromozione Lombardia Sito Internethttp://www.crlombardia.it StoriaFondazione1991 Detentore Vogherese Tritium Cast Brescia Record vittorie Corbetta Romanese S...

Hati Kudus Yesus. Bagian dari seri Gereja Katolik tentangDevosi kepada YesusKristus Pantokrator Devosi Lima Luka Suci Hati Kudus Yesus Wajah Kudus Yesus Kerahiman Ilahi Adorasi Ekaristi Nama Yesus Yang Tersuci Waktu Suci Tindakan Reparasi kepada Yesus Jalan Salib Darah Kristus Kanak-kanak Yesus dari Praha Doa Anima Christi Luka di Bahu Yesus Persembahan harian pagi Doa konsekrasi Tindakan konsekrasi Engkaulah Kristus Doa Vianney Doa Perboyre Doa Montfort Doa Salib Portal Katoliklbs ...

Filippo Tortu Filippo Tortu ai Giochi del Mediterraneo 2018 Nazionalità Italia Altezza 187 cm Peso 75 kg Atletica leggera Specialità Velocità Società Fiamme Gialle Record 60 m 658 (indoor - 2019) 100 m 999 (2018) 200 m 2010 (2022) 4×100 m 3750 (2021) CarrieraSocietà 2006-2008 Polisportiva Besanese2009-2010 Atletica Vis Nova Giussano2011-2015 Atletica Riccardi2015- Fiamme GialleNazionale 2016- Italia16Palmarès Competizione Ori Argenti Bronzi Giochi olimpici 1 0 0 Mondi...

Newspaper from Ecuador El ComercioTypeDaily newspaperFormatBroadsheetOwner(s)Grupo El Comercio C. A.Editor-in-chiefNoneEditorNoneFounded1906Political alignmentCenter-rightConservativeLanguageSpanishHeadquartersAvenida Pedro Vicente Maldonado 11515. Quito, EcuadorCirculation40.000 Daily 78.000 SundayWebsiteelcomercio.com El Comercio was a daily Ecuadorian newspaper in Quito. It covers news from inside and outside the country, although its focus is primarily on the former, especially on Quito, ...

Villafallettocomune Villafalletto – VedutaUna vista di Villafalletto LocalizzazioneStato Italia Regione Piemonte Provincia Cuneo AmministrazioneSindacoGiuseppe Sarcinelli (lista civica) dal 26-5-2014 TerritorioCoordinate44°33′N 7°32′E / 44.55°N 7.533333°E44.55; 7.533333 (Villafalletto)Coordinate: 44°33′N 7°32′E / 44.55°N 7.533333°E44.55; 7.533333 (Villafalletto) Altitudine431 m s.l.m. Superficie29,73 km...

Навчально-науковий інститут інноваційних освітніх технологій Західноукраїнського національного університету Герб навчально-наукового інституту інноваційних освітніх технологій ЗУНУ Скорочена назва ННІІОТ ЗУНУ Основні дані Засновано 2013 Заклад Західноукраїнський �...

Camera dei rappresentanti, 1900 circa Camera dei signori, 1900 circa Il Landtag prussiano (in tedesco: Preußischer Landtag, letteralmente Dieta territoriale prussiana) era l'assemblea rappresentativa del Regno di Prussia. Istituito nel 1849, era un'assemblea legislativa bicamerale composta dalla Camera dei signori (Herrenhaus), la camera alta, e dalla Camera dei rappresentanti (Abgeordnetenhaus), la camera bassa. Dopo la prima guerra mondiale e la rivoluzione di novembre il Landtag continuò...

Pemilihan umum federal Jerman Barat 19531949195706 September 1953 (1953-09-06)[1]Seluruh 509 kursi dalam Bundestag255 kursi untuk meraih status mayoritasKehadiran pemilih86.0% (suara layak)[2]Kandidat Partai pertama Partai kedua Partai ketiga Ketua Konrad Adenauer Erich Ollenhauer Franz Blücher Partai CDU/CSU SPD FDP Kursi sebelumnya 144 140 57 Kursi yang dimenangkan 249 162 53 Perubahan kursi 105 22 4 Suara Populer 12,443,981 7,94...

Konferensi Waligereja Korea한국천주교주교회의SingkatanCBCKTanggal pendirianMaret 1857TipeKonferensi waligerejaKantor pusatSeoul, Korea SelatanJumlah anggota Uskup Katolik KoreaPresidenMatthias Ri Iong-hoonWakil-PresidenBasil Cho Kyu-manOrganisasi indukGereja Katolik RomaSitus webwww.cbck.or.kr Konferensi Waligereja Korea adalah konferensi waligereja Katolik di Korea, membawahi baik Gereja Katolik di Korea Utara maupun Korea Selatan.[1] Daftar presiden Thomas F. Quinlan,...

Family FeudLogo di Family Feud dal 2007PaeseStati Uniti d'America Anno1976 – in produzione Generegame show Edizioni18 Puntate407 Durata22–26 min (puntata): ABC (1976–85) CBS (1988–92) syndication (1977–85, 1988–95, 1999–presente) 42–44 min (puntata): Speciali ABC (1979–84, 2015–presente) CBS (1992–93 syndication (1994–95) Lingua originaleinglese Rapporto1,78:1 RealizzazioneConduttoreRichard Dawson (1976–85, 1994–95)Ray Combs (1988–94)Louie Anderson (1999–2002)R...

井田 完二(いだ かんじ[1]、1897年(明治30年)3月23日[2] - 1988年(昭和63年)[3])は、日本の内務官僚。従六位[4]。井田特許事務所長[1][5]。 経歴 福井県遠敷郡雲浜村(現:小浜市)生まれ[4]。井田謙治の二男[6][7]。日本加除出版取締役・井田勝久(井田耕治)の弟[8][9]。1922年[6]、高文行政科に合格す...

Suresnes Vue de Suresnes depuis la terrasse du Fécheray, avec le bois de Boulogne et la tour Eiffel en arrière-plan. Blason Logo Administration Pays France Région Île-de-France Département Hauts-de-Seine Arrondissement Nanterre Intercommunalité Métropole du Grand ParisEPT Paris Ouest La Défense Maire Mandat Guillaume Boudy (LR) 2020-2026 Code postal 92150 Code commune 92073 Démographie Gentilé Suresnois Populationmunicipale 49 104 hab. (2021 ) Densité 12 956 ha...

Ministry of the Government of Pakistan Ministry of Kashmir Affairs and Gilgit-Baltistanوزارت امور کشمیر و گلگت بلتستانAgency overviewFormedApril 1949JurisdictionGovernment of PakistanHeadquartersIslamabad, Islamabad Capital Territory, PakistanEmployees173 (58 officers, 115 staff members)Annual budget₨.80 crore (US$5 million) (2018–19)Minister responsibleEngr Amir MuqamAgency executiveTariq Mahmood Pasha, Federal SecretaryChild agenciesK & GB WingPlanning Wing...

Sacred motet attributed to Johann Kuhnau Tristis est anima meaSacred motet by Johann Kuhnau (attrib.)Christ and His Disciples in the Garden of Gethsemane (Rembrandt)EnglishMy soul is exceedingly sorrowfulKeyF minorOccasionMaundy ThursdayTextMatthew 26:38LanguageLatinVocalSSATB Tristis est anima mea (Sad is my soul) is a sacred motet for five voices attributed to Johann Kuhnau, Thomaskantor in Leipzig. The text is the second responsory at Tenebrae for Maundy Thursday, one of the Latin ...

Le Jamaïcain Usain Bolt détient les records olympiques masculins du 100 m, du 200 m et du relais 4 × 100 m. Les records olympiques d'athlétisme constituent la meilleure performance jamais réalisée par un athlète dans le cadre des Jeux olympiques d'été. Ils sont homologués par le Comité international olympique (CIO) depuis la première édition des Jeux olympiques, en 1896. Le plus ancien record olympique est celui de l'Américain Bob Beamon qui établit la marque de 8,90&...
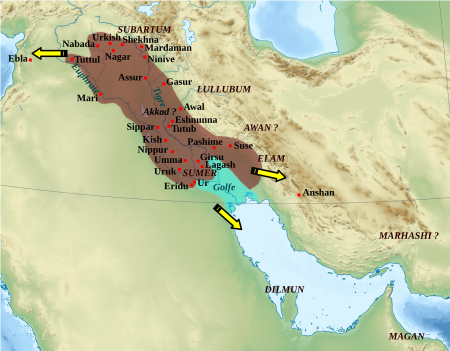
Bronze age city-state mentioned in the Armana Letters The Akkadian Empire under Naram-Sin, Subartu is shown north. The land of Subartu (Akkadian Šubartum/Subartum/ina Šú-ba-ri, Assyrian mât Šubarri) or Subar (Sumerian Su-bir4/Subar/Šubur, Ugaritic 𐎘𐎁𐎗 ṯbr) is mentioned in Bronze Age literature. The name also appears as Subari in the Amarna letters, and, in the form Šbr, in Ugarit. Subartu was apparently a kingdom in Upper Mesopotamia, at the upper Tigris and later it referre...






