Експоненційний розпад
|
Read other articles:

This article needs additional citations for verification. Please help improve this article by adding citations to reliable sources. Unsourced material may be challenged and removed.Find sources: Logos and uniforms of the Los Angeles Lakers – news · newspapers · books · scholar · JSTOR (March 2019) (Learn how and when to remove this template message) The logos and uniforms of the Los Angeles Lakers have gone through many changes throughout the history o...

Australian soccer player Sally Shipard Personal informationFull name Sally Jean ShipardDate of birth (1987-10-20) 20 October 1987 (age 36)Place of birth Tumut, AustraliaHeight 1.74 m (5 ft 9 in)Position(s) Central midfielderYouth career Wagga PCYCSenior career*Years Team Apps (Gls)2009–2014 Canberra United 30 (4)2012 → Bayer Leverkusen (loan) 10 (0)Total 40 (4)International career2004–2006 Australia U-20 17 (4)2004–2011 Australia 59 (4) *Club domestic league appear...

Mountain peak southwest of Lake Tahoe, El Dorado county in California, U.S.A. Mount TallacNortheast aspectHighest pointElevation9,739 ft (2,968 m) NAVD 88[1]Prominence695 ft (212 m)[2]Parent peakDicks Peak (9,974 ft)[3]Isolation2.82 mi (4.54 km)[3]ListingTahoe OGUL Star Peak[4]Sierra Peaks Section[5]Coordinates38°54′21.5″N 120°05′56.3″W / 38.905972°N 120.098972°W / ...

Hsuan Hua宣化Hsuan Hua di Ukiah, California GelarMaster Chan, Pendiri dan Biarawan Kota Sepuluh Ribu Buddha, Presiden Dharma Realm Buddhist Association, Rektor Dharma Realm Buddhist UniversityInformasi pribadiLahir(1918-04-16)16 April 1918Provinsi Jilin, ChinaMeninggal7 Juni 1995(1995-06-07) (umur 77)Los Angeles, California, Amerika SerikatAgamaBuddha ChanKebangsaanTiongkokMazhabSekolah Chan HuiyangSilsilahGenerasi ke-9Kedudukan seniorGuruHsu Yun Siswa Heng Sure, Heng Lyu, Heng Chau, H...

Department of Colombia For other uses, see Cauca (disambiguation). This article relies largely or entirely on a single source. Relevant discussion may be found on the talk page. Please help improve this article by introducing citations to additional sources.Find sources: Cauca Department – news · newspapers · books · scholar · JSTOR (March 2009) Department in Andean Region/Pacific Region, ColombiaDepartment of Cauca Departamento del CaucaDepartment Fla...

The CroodsSutradaraKirk DeMiccoChris SandersProduserKristine BensonJane HartwellSkenarioKirk DeMiccoChris SandersCeritaJohn Cleese[1]Kirk DeMiccoChris SandersPemeranNicolas CageEmma StoneRyan ReynoldsCatherine KeenerClark DukeCloris LeachmanNaratorEmma StonePenata musikAlan Silvestri[2]SinematograferYong Duk JhunPenyuntingEric DapkewiczDarren T. HolmesPerusahaanproduksiDreamWorks AnimationDistributor20th Century FoxTanggal rilis 15 Februari 2013 22 Maret 2013Durasi98 men...

Species of fish American eel Conservation status Endangered (IUCN 3.1)[1] Scientific classification Domain: Eukaryota Kingdom: Animalia Phylum: Chordata Class: Actinopterygii Order: Anguilliformes Family: Anguillidae Genus: Anguilla Species: A. rostrata Binomial name Anguilla rostrataLesueur, 1821 Range map Synonyms Leptocephalus grassii The American eel (Anguilla rostrata) is a facultative catadromous fish found on the eastern coast of North America. Freshwater eels are fi...

Pour les articles homonymes, voir Müller. Adam MüllerAdam Müller.BiographieNaissance 30 juin 1779BerlinDécès 17 janvier 1829 (à 49 ans)VienneSépulture Cimetière AssistensNationalité prussienneFormation Université de GöttingenActivités Écrivain, critique littéraire, journaliste d'opinion, économiste, philosophe, homme politiquemodifier - modifier le code - modifier Wikidata Adam Heinrich Müller (né à Berlin, le 30 juin 1779 et mort à Vienne, le 17 janvier 1829) est un ...
Die Liste der technischen Denkmale im Landkreis Mittelsachsen enthält die Technischen Denkmale im Landkreis Mittelsachsen.[Anm. 1] Diese Liste ist eine Teilliste der Liste der Kulturdenkmale in Sachsen. Aufgrund der großen Anzahl von technischen Denkmalen ist die Liste aufgeteilt in die Liste der technischen Denkmale im Landkreis Mittelsachsen (A–E) Liste der technischen Denkmale im Landkreis Mittelsachsen (F–G) Liste der technischen Denkmale im Landkreis Mittelsachsen (H–N) L...

American javelin thrower Lynda SutfinPersonal informationNationalityAmericanBorn (1962-10-06) October 6, 1962 (age 61)SportSportAthleticsEventJavelin throw Lynda Sutfin (born October 6, 1962) is an American athlete. She competed in the women's javelin throw at the 1984 Summer Olympics and the 1988 Summer Olympics.[1] References ^ Evans, Hilary; Gjerde, Arild; Heijmans, Jeroen; Mallon, Bill; et al. Lynda Sutfin Olympic Results. Olympics at Sports-Reference.com. Sports Referen...

TUSC redirects here. For the auto racing series, see TUDOR United SportsCar Championship. The subject of this article is participating in the 2024 general election to the House of Commons of the United Kingdom on 4 July, and has had no MPs in the House of Commons since Parliament was dissolved on 30 May. Some parts of this article may be out of date during this period. Please feel free to improve this article (but note that updates without valid and reliable references will be remov...

Charlotta BergerBorn(1784-08-21)21 August 1784Linköping, SwedenDied25 May 1852(1852-05-25) (aged 67)Linköping, SwedenOccupation(s)Writer, translator, poet, songwriter Christina Charlotta Ulrika Berger, née Cronhielm af Hakunge (21 August 1784 – 25 May 1852), was a Swedish writer, translator, poet and songwriter. Life Charlotta Berger was born in Linköping, the daughter of the major count Carl Emil Cronhielm af Hakunge and Hedvig Ulrika Boije af Gennäs, and the sister of the polit...

Soviet unmanned Progress cargo spacecraft Progress 12A Progress 7K-TG spacecraftMission typeSalyut 6 resupplyCOSPAR ID1981-007A SATCAT no.12152[1] Spacecraft propertiesSpacecraftProgress (No.113)Spacecraft typeProgress 7K-TG[2]ManufacturerNPO Energia Start of missionLaunch date24 January 1981, 14:18:02 UTC[1]RocketSoyuz-U[2]Launch siteBaikonur, Site 1/5 End of missionDisposalDeorbitedDecay date20 March 1981, 16:59 UTC[3] Orbital parametersReference ...

سفارة البوسنة والهرسك في الولايات المتحدة البوسنة والهرسك الولايات المتحدة الإحداثيات 38°53′46″N 77°02′50″W / 38.8961°N 77.0472°W / 38.8961; -77.0472 البلد الولايات المتحدة المكان شمال غربي واشنطن العاصمة الاختصاص الولايات المتحدة، والبرازيل[1] الموقع الالكتروني ...

Parshvanatha temple, Khajuraho, a UNESCO World Heritage Site Part of a series onJainism Jains History Timeline Index Philosophy Anekantavada Cosmology Ahimsa Karma Dharma Mokṣa Kevala Jnana Dravya Tattva Brahmacarya Aparigraha Gunasthana Saṃsāra EthicsEthics of Jainism Mahavratas (major vows) Ahiṃsā (non-violence) Satya (truth) Asteya (non-stealing) Brahmacarya (chastity) Aparigraha (non-possession) Anuvratas (further vows) Sāmāyika Sallekhana Jain prayers Bhaktamara Stotra Miccham...

Period of Japanese history (1096-1097 AD) Part of a series on theHistory of Japan ListPaleolithicbefore 14,000 BCJōmon14,000 – 1000 BCYayoi 1000 BC – 300 ADKofun 300 AD – 538 ADAsuka 538 – 710Nara 710 – 794HeianFormer Nine Years' WarLater Three-Year WarGenpei War 794–1185KamakuraJōkyū WarMongol invasionsGenkō WarKenmu Restoration 1185–1333MuromachiNanboku-chō periodSengoku period 1336–1573Azuchi–Momoyama Nanban tradeImjin WarBattle of Sek...
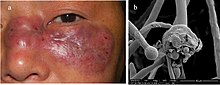
Si ce bandeau n'est plus pertinent, retirez-le. Cliquez ici pour en savoir plus. La mise en forme de cet article est à améliorer (juin 2021). La mise en forme du texte ne suit pas les recommandations de Wikipédia : il faut le « wikifier ». Pour l’article homonyme, voir Champignon noir. Un homme de 47 ans atteint de mucormycose et micrographie électronique de sa peau montrant des sporanges de champignons de l'ordre des Mucorales. La mucormycose associée à la COVID-19[1...

Odlum Brown Vancouver Open 2008Sport Tennis Data28 luglio - 3 agosto Edizione4ª (maschile) CampioniSingolare Dudi Sela Doppio Eric Butorac / Travis Parrott 2007 2009 L'Odlum Brown Vancouver Open 2008 è stato un torneo di tennis facente parte della categoria ATP Challenger Series nell'ambito dell'ATP Challenger Series 2008. Il torneo si è giocato a Vancouver in Canada dal 28 luglio al 3 agosto 2008 su campi in cemento e aveva un montepremi di $100 000. Indice 1 Vincitori 1.1 Singolare 1.2 D...

Apung pasir Anthus richardi In ThailandStatus konservasiRisiko rendahIUCN103821389 TaksonomiKelasAvesOrdoPasseriformesSuperfamiliPasseroideaFamiliMotacillidaeGenusAnthusSpesiesAnthus richardi Vieillot, 1818 Apung pasir (Anthus richardi) adalah burung pengicau berukuran sedang yang berkembang biak di padang rumput terbuka di Palearctic Timur. Ini adalah migran jarak jauh yang pindah ke dataran rendah terbuka di anak benua India dan Asia Tenggara. Ini adalah gelandangan yang jarang namun biasa ...

RivarossafrazioneRivarossa – VedutaL'entrata a Rivarossa da sud LocalizzazioneStato Italia Regione Piemonte Provincia Alessandria ComuneBorghetto di Borbera TerritorioCoordinate44°43′49″N 8°56′40″E44°43′49″N, 8°56′40″E (Rivarossa) Altitudine738 m s.l.m. Abitanti0[2] Altre informazioniCod. postale15060 Prefisso0143 Fuso orarioUTC+1 CartografiaRivarossa Modifica dati su Wikidata · Manuale Rivarossa è una frazione abbandonata del com...




















