Граф товаришування
| |||||||||||||||||||||
Read other articles:

Arbi SanitLahir(1939-06-04)4 Juni 1939Painan, Pesisir Selatan, Sumatera Barat, Hindia BelandaMeninggal25 Maret 2021(2021-03-25) (umur 81)Jakarta, IndonesiaKebangsaanIndonesiaPekerjaanIlmuwan, DosenSuami/istriAyunis Samah[1]AnakAlfar Yusar Sanit[2] Drs. Arbi Sanit (4 Juni 1939 – 25 Maret 2021) merupakan salah seorang ilmuwan politik Indonesia. Arbi pernah menjadi dosen ilmu politik di Universitas Indonesia dan Universitas Muhammadiyah Prof Dr Hamka.[3&...

Lokasi Masjid terkait dengan benteng dan istana Ázm Bab al-Jabiyah (Arab: بَابُ الْجَابِيَّةِ, romanized: Bāb al-Jābīyahcode: ar is deprecated ; Gate of the Water Trough) adalah salah satu air dari tujuh gerbang kota kuno yang berada di Damaskus, Suriah. Selama era Romawi, gerbang itu didedikasikan untuk Mars.[1] Bab al-Jabiya adalah pintu masuk utama yang ada di sisi barat kota. Gerbang itu berada di Midhat Pasha Souq (bazar) yang mana merupakan bagian dari...
Pour les articles homonymes, voir Al-Hadi. Si ce bandeau n'est plus pertinent, retirez-le. Cliquez ici pour en savoir plus. Certaines informations figurant dans cet article ou cette section devraient être mieux reliées aux sources mentionnées dans les sections « Bibliographie », « Sources » ou « Liens externes » (janvier 2020). Vous pouvez améliorer la vérifiabilité en associant ces informations à des références à l'aide d'appels de notes. Al-Had...

Confessions of a Dangerous MindPoster rilis layar lebarSutradaraGeorge ClooneyProduserAndrew LazarSkenarioCharlie KaufmanBerdasarkanConfessions of a Dangerous Mindoleh Chuck BarrisPemeranDrew BarrymoreGeorge ClooneyJulia RobertsSam RockwellPenata musikAlex WurmanSinematograferNewton Thomas SigelPenyuntingStephen MirrionePerusahaanproduksiMad Chance DistributorMiramaxTanggal rilis 31 Desember 2002 (2002-12-31) (Perilisan terbatas) 24 Januari 2003 (2003-01-24) Durasi113 meni...

Greek professional diver (born 1964) Aristotelis ZervoudisΑριστοτέλης ΖερβούδηςA. Zervoudis in the ceremony of his appointment as Cavaliere dell' Ordine della Stella d' Italia in June 2018Born1964Athens, GreeceOccupationprofessional diver Aristotelis (Telis) Zervoudis (Greek: Αριστοτέλης Ζερβούδης; b. in Athens in 1964) is a professional diver from Greece. Notable discoveries During his diving expeditions he discovered and identified several important w...

Cryptographic attack on the ssh protocol Terrapin attackLogo for the Terrapin attackCVE identifier(s)CVE-2023-48795Date discovered19 December 2023; 4 months ago (2023-12-19)DiscovererFabian Bäumer, Marcus Brinkmann, Jörg Schwenk (Ruhr University Bochum)Affected softwareimplementations of the Secure Shell (SSH) protocol including OpenSSHWebsitehttps://terrapin-attack.com/ The Terrapin attack is a cryptographic attack on the commonly used SSH protocol that is used for secure...

Cercle Arctique T. Cancer Équateur T. Capricorne Cercle AntarctiqueTracé du méridien de 84° est En géographie, le 84e méridien est est le méridien joignant les points de la surface de la Terre dont la longitude est égale à 84° est. Géographie Dimensions Comme tous les autres méridiens, la longueur du 84e méridien correspond à une demi-circonférence terrestre, soit 20 003,932 km. Au niveau de l'équateur, il est distant du méridien de Greenwich de 9 35...

La Sinistra LeaderNicola FratoianniMaurizio Acerbo Stato Italia AbbreviazioneLS, Sinistra Fondazionefebbraio 2019 Dissoluzionesettembre 2019 Partito Sinistra Italiana èViva Partito del Sud PRC-SE IdeologiaSocialismo democratico[1]Ecosocialismo[1]MeridionalismoAmbientalismoPacifismoLaicismo CollocazioneSinistra[2] Partito europeoPartito della Sinistra Europea Gruppo parl. europeoGUE/NGL Seggi massimi Europarlamento0 / 76 Sito webla-sinistra.it ...

「俄亥俄」重定向至此。关于其他用法,请见「俄亥俄 (消歧义)」。 俄亥俄州 美國联邦州State of Ohio 州旗州徽綽號:七葉果之州地图中高亮部分为俄亥俄州坐标:38°27'N-41°58'N, 80°32'W-84°49'W国家 美國加入聯邦1803年3月1日,在1953年8月7日追溯頒定(第17个加入联邦)首府哥倫布(及最大城市)政府 • 州长(英语:List of Governors of {{{Name}}}]]) •&...

2007 compilation album by Trill Fam, Lil Boosie, Webbie, FoxxTrill Entertainment Presents: Survival of the FittestCompilation album by Trill Fam, Lil Boosie, Webbie, FoxxReleasedMarch 24, 2007 (2007-03-24)Recorded2006–07GenreSouthern hip hopgangsta rapLength1:07:49LabelTrill EntertainmentProducerTurk (exec.)Mel (exec.)BJMouseTrill Fam chronology Trill Entertainment Presents: Survival of the Fittest(2007) Trill Entertainment Presents: All or Nothing(2010) Lil Boosie ch...

رايخ ماركمعلومات عامةالبلد جمهورية فايمار ألمانيا النازية المنطقة جمهورية فايمار — ألمانيا النازية تاريخ الإصدار 30 أغسطس 1924 عوض رنتتن مارك (24 أغسطس 1924) عوضه مارك ألماني (21 يونيو 1948)مارك ألماني (24 يونيو 1948)مارك ألماني شرقي (24 يونيو 1948)مارك ساري (16 يونيو 1947) رمز العملة ℛℳ المص...
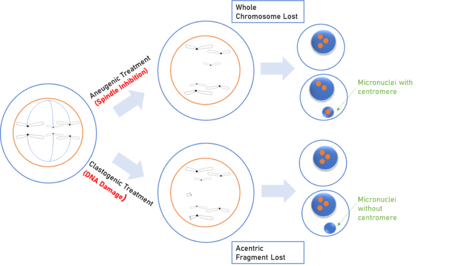
Cet article est une ébauche concernant la biologie cellulaire et moléculaire. Vous pouvez partager vos connaissances en l’améliorant (comment ?) selon les recommandations des projets correspondants. Figure comparant les effets de l'exposition à des agents génotoxiques (aneugènes et clastogènes) sur l'ADN. Les aneugènes induisent une mauvaise ségrégation des chromosomes dans les cellules filles, tandis que les clastogènes cassent l'ADN et les chromosomes. Un clastogène est ...

1814 Connecticut gubernatorial election 1814 Connecticut gubernatorial election ← 1813 April 11, 1814 1815 → Nominee John Cotton Smith Elijah Boardman Party Federalist Democratic-Republican Popular vote 9,415 2,619 Percentage 72.87% 20.27% County results Smith: 70–80% >90% No data Governor before election John Cotton Smith Federalist Elected Governor John Cotton Smit...

「Let's try again」チーム・アミューズ!! の シングルリリース 2011年5月25日 日本規格 デジタル・ダウンロード12cmCD録音 2011年VICTOR STUDIO[1]ジャンル J-POP時間 9分2秒レーベル アミューズソフトエンタテインメント(ASCM-6092)作詞・作曲 桑田佳祐(オリジナル部分)ゴールドディスク プラチナ(日本レコード協会)[2]チャート最高順位 週間2位(オリコン)[3] ...

For the BRT station, see Tecámac (Mexibús). Town & Municipality in State of Mexico ----, MexicoTecámacTown & Municipality SealLocation of the municipality in Mexico StateTecámacLocation in MexicoCoordinates: 19°42′47″N 98°58′06″W / 19.71306°N 98.96833°W / 19.71306; -98.96833Country MexicoState State of Mexico RegionEcatepec RegionMetro areaGreater Mexico CityMunicipal StatusSeptember 12, 1825[1]Municipal SeatTecámac de Felipe Villa...

Manufacture of electromagnetic coils This article needs additional citations for verification. Please help improve this article by adding citations to reliable sources. Unsourced material may be challenged and removed.Find sources: Coil winding technology – news · newspapers · books · scholar · JSTOR (July 2016) (Learn how and when to remove this message) In electrical engineering, coil winding is the manufacture of electromagnetic coils. Coils are use...

English squash player Lee BeachillLee Beachill with his 2005 US Open trophyFull nameLee BeachillCountry EnglandResidencePontefract, EnglandBorn (1977-11-28) 28 November 1977 (age 46)Huddersfield, EnglandHeight1.82 m (6 ft 0 in)Weight76 kg (168 lb)Turned Pro1998Retired2009PlaysRight HandedCoached byMalcolm WillstropRacquet usedDunlopMen's singlesHighest rankingNo. 1 (October 2004)Title(s)8Tour final(s)13World OpenF (2004) Medal r...

Pour les articles homonymes, voir Frossard. Si ce bandeau n'est plus pertinent, retirez-le. Cliquez ici pour en savoir plus. Cet article ne cite pas suffisamment ses sources (septembre 2017). Si vous disposez d'ouvrages ou d'articles de référence ou si vous connaissez des sites web de qualité traitant du thème abordé ici, merci de compléter l'article en donnant les références utiles à sa vérifiabilité et en les liant à la section « Notes et références ». En pratique...

私はいったい、何と闘っているのか著者 つぶやきシロー発行日 2016年10月26日発行元 小学館国 日本言語 日本語ページ数 272コード ISBN 9784093864510 ウィキポータル 文学 [ ウィキデータ項目を編集 ]テンプレートを表示 『私はいったい、何と闘っているのか』(わたしはいったい、なにとたたかっているのか)は、つぶやきシローの小説。単行本は2016年10月26日に小学館より�...

Christianity as practiced by the ancient Goths This article needs additional citations for verification. Please help improve this article by adding citations to reliable sources. Unsourced material may be challenged and removed.Find sources: Gothic Christianity – news · newspapers · books · scholar · JSTOR (July 2007) (Learn how and when to remove this message) Part of a series of articles onArianism History and theology Arius Acacians Anomoeanism Aria...





