Гвинтівка Спрінгфілд
|
Read other articles:

Ratu & FriendsAlbum kompilasi karya RatuDirilis30 Agustus 2005Direkam2005GenrePop, Pop rock, Rock, Rock elektronikDurasi47:57LabelSony BMG Music Entertainment IndonesiaProduserMaia AhmadKronologi Ratu Bersama (2003)Bersama2003 Ratu & Friends (2005) No. Satu (2006)No. Satu2006 Ratu & Friends adalah album kompilasi karya Ratu yang dirilis tahun 2005. Album ini merupakan album pemanasan Ratu bersama vokalis barunya Mulan Jameela. Album ini merupakan kompilasi yang hanya memuat du...

American diplomat (1909–1997) Douglas MacArthur IIUnited States Ambassador to IranIn officeOctober 13, 1969 – February 17, 1972PresidentRichard NixonPreceded byArmin H. MeyerSucceeded byJoseph S. FarlandUnited States Ambassador to AustriaIn officeMay 24, 1967 – September 16, 1969PresidentLyndon B. JohnsonRichard NixonPreceded byJames Williams RiddlebergerSucceeded byJohn P. HumesAssistant Secretary of State for Legislative AffairsIn officeMarch 14, 1965 – Ma...

Lee JiyeonInformasi latar belakangNama lainLee JiyeonLahir18 Februari 1984 (umur 40)GenreK-PopPekerjaanpenyanyi, penariTahun aktif2002–sekarangLabelSM EntertainmentArtis terkaitIsak N Jiyeon (2002-2004)The Grace (2005-sekarang)SM Town Lee Jiyeon (lahir 18 Februari 1984) adalah penyanyi dan penari Korea Selatan. Ia tergabung dalam duo R&B Isak N Jiyeon sebagai Lee Jiyeon dari 2002-2004. Dan kemudian bergabung bersama The Grace sebagai Lina dari 2005-sekarang. Diskografi Isak N Jiyeo...

1926 United States Senate election in North Carolina ← 1920 November 2, 1926 1932 → Nominee Lee Overman Johnson Jay Hayes Party Democratic Republican Popular vote 218,934 142,891 Percentage 60.51% 39.49% Senator before election Lee Slater Overman Democratic Elected Senator Lee Slater Overman Democratic Elections in North Carolina Federal government U.S. President 1792 1796 1800 1804 1808 1812 1816 1820 1824 1828 1832 1836 1840 1844 1848 1852 1856 1860 1868 1...

Spice from the inner tree bark of several members of genus Cinnamomum This article is about the spice. For the genus of trees where cinnamon originates, see Cinnamomum. For other uses, see Cinnamon (disambiguation). Dried bark strips, bark powder and flowers of the small tree Cinnamomum verum Cinnamon is a spice obtained from the inner bark of several tree species from the genus Cinnamomum. Cinnamon is used mainly as an aromatic condiment and flavouring additive in a wide variety of cuisines,...
Carentino commune di Italia Tempat Negara berdaulatItaliaRegion di ItaliaPiedmontProvinsi di ItaliaProvinsi Alessandria NegaraItalia Ibu kotaCarentino PendudukTotal330 (2023 )GeografiLuas wilayah9,79 km² [convert: unit tak dikenal]Ketinggian160 m Berbatasan denganBergamasco Borgoratto Alessandrino Bruno Frascaro Gamalero Mombaruzzo Oviglio SejarahHari liburpatronal festival Santo pelindungMaria Diangkat ke Surga Informasi tambahanKode pos15022 Zona waktuUTC+1 UTC+2 Kode telepon013...

William Blackstone William Blackstone (Londra, 10 luglio 1723 – Wallingford, 14 febbraio 1780) è stato un giurista britannico, professore presso l'Università di Oxford dal 1758 al 1766. Biografia Figlio di un commerciante di seta, effettuò gli studi ad Oxford, presso il Pembroke College e divenne in seguito, nel 1746, barrister, cioè avvocato abilitato a trattare casi davanti a corti di livello superiore, professione che esercitò presso le Corti di Westminster per alcuni anni senza ott...

Family of birds JacanasTemporal range: Oligocene to recent Comb-crested jacana (Irediparra gallinacea) Scientific classification Domain: Eukaryota Kingdom: Animalia Phylum: Chordata Class: Aves Order: Charadriiformes Suborder: Scolopaci Family: JacanidaeChenu & des Murs, 1854 Type genus Jacana Genera Microparra Actophilornis Irediparra Hydrophasianus Metopidius Jacana Synonyms Parridae The jacanas (sometimes referred to as Jesus birds or lily trotters) are a group of tropical waders in th...
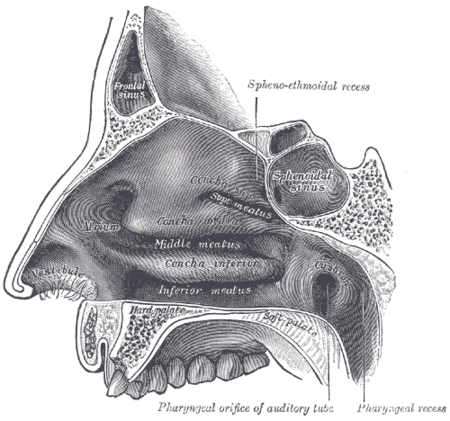
Disambiguazione – Se stai cercando il significato relativo all'araldica, vedi Palato (araldica). Questa voce o sezione sull'argomento anatomia è priva o carente di note e riferimenti bibliografici puntuali. Sebbene vi siano una bibliografia e/o dei collegamenti esterni, manca la contestualizzazione delle fonti con note a piè di pagina o altri riferimenti precisi che indichino puntualmente la provenienza delle informazioni. Puoi migliorare questa voce citando le fonti più precisamen...

British electric multiple unit British Rail Class 803Lumo Class 803 at Edinburgh WaverleyInterior of a Class 803 unitIn service2021–presentManufacturerHitachi RailBuilt atKasado Works, Kudamatsu, Japan[1]Newton Aycliffe Manufacturing Facility, EnglandFamily nameA-trainConstructed2020–2021Entered service25 October 2021 (2021-10-25)Number built5Formation5 cars per unit: DPTS-MS-MS-MS-DPTS[2]Fleet numbers803001–803005Capacity402 seats[3]Operat...

Red 2Logo ufficiale del filmLingua originaleinglese Paese di produzioneStati Uniti d'America Anno2013 Durata116 min Rapporto2,35:1 Genereazione, commedia RegiaDean Parisot Soggettopersonaggi creati da Warren Ellis e Cully Hamner SceneggiaturaErich Hoeber, Jon Hoeber ProduttoreLorenzo di Bonaventura, Mark Vahradian, Raphaël Benoliel, Alexander Dostal, Cliff Lanning Produttore esecutivoJake Myers, David Ready, John Brooks Klingenbeck Casa di produzioneDC Entertainment, Di Bonaventura Pictu...

Kawasan Metropolitan Medan Medan RayaMebidangroKawasan metropolitanDari atas, kiri ke kanan: Panorama Kota Medan, Gapura Selamat Datang Kota Binjai, Museum Deli Serdang, Gunung Sinabung, dan Pemandangan Danau Lau KawarNegara IndonesiaProvinsi Sumatera UtaraKota intiMedanDaerah penyangga Kota Binjai Kabupaten Deli Serdang Kabupaten Karo Tanggal peresmian6 November 2011Dasar hukumPeraturan Presiden №62 tahun 2011Zona waktuUTC+07:00 (WIB)Kode area telepon+6261 Mebidangro (akronim dar...

Artikel ini bukan mengenai Inuyasha. InuyashikiSampul volume pertamaいぬやしきGenreHoror tubuh, fiksi ilmiah, pahlawan super[1][2] MangaPengarangHiroya OkuPenerbitKodanshaPenerbit bahasa InggrisNA Kodansha USA (print)Crunchyroll (digital)MajalahEveningDemografiSeinenTerbitJanuari 2014 – Juli 2017Volume10 (Daftar volume) Seri animeSutradaraKeiichi SatoShuhei YabutaSkenarioHiroshi SekoMusikYoshihiro IkeStudioMAPPAPelisensiAmazon (streaming)SaluranasliFuji TV (Noitamina)Ta...

American documentary television series This article includes a list of general references, but it lacks sufficient corresponding inline citations. Please help to improve this article by introducing more precise citations. (March 2020) (Learn how and when to remove this message) The Curse of Civil War GoldGenreRealityNarrated byRobert ClotworthyCountry of originUnited StatesOriginal languageEnglishNo. of seasons2No. of episodes16ProductionCamera setupMultipleRunning time43 minutesProduction co...

Railway museum in Kyoto, Japan Kyoto Railway Museum京都鉄道博物館The museum entrance in October 2016Location of the museumShow map of Kyoto cityKyoto Railway Museum (Japan)Show map of JapanFormer nameUmekoji Steam Locomotive MuseumEstablished October 10, 1972 (1972-10-10) (as Umekoji Steam Locomotive Museum) April 29, 2016 (2016-04-29) (as Kyoto Railway Museum) LocationShimogyō-ku, Kyoto, JapanCoordinates34°59′14″N 135°44′33″E / ...

Hungarian opera singer (1886–1946) You can help expand this article with text translated from the corresponding article in Hungarian. (June 2022) Click [show] for important translation instructions. View a machine-translated version of the Hungarian article. Machine translation, like DeepL or Google Translate, is a useful starting point for translations, but translators must revise errors as necessary and confirm that the translation is accurate, rather than simply copy-pasting machine...

In general topology, a branch of mathematics, a non-empty family A of subsets of a set X {\displaystyle X} is said to have the finite intersection property (FIP) if the intersection over any finite subcollection of A {\displaystyle A} is non-empty. It has the strong finite intersection property (SFIP) if the intersection over any finite subcollection of A {\displaystyle A} is infinite. Sets with the finite intersection property are also called centered systems and filter subbases.[1] ...

此條目介紹的是绝对君主制容许民众有一定权力的一种形式。关于保证个人自由的独裁政体,请见「软性独裁政体(英语:Dictablanda)」。关于为全体人民利益而行使绝对政治权力的独裁政体,请见「仁慈独裁(英语:Benevolent dictatorship)」。 此條目可参照英語維基百科相應條目来扩充。若您熟悉来源语言和主题,请协助参考外语维基百科扩充条目。请勿直接提交机...

Protein-coding gene in the species Homo sapiens NFATC2Available structuresPDBOrtholog search: PDBe RCSB List of PDB id codes1A02, 1OWR, 1P7H, 1PZU, 2AS5, 2O93, 3QRFIdentifiersAliasesNFATC2, NFAT1, NFATP, nuclear factor of activated T-cells 2, nuclear factor of activated T cells 2External IDsOMIM: 600490; MGI: 102463; HomoloGene: 7861; GeneCards: NFATC2; OMA:NFATC2 - orthologsGene location (Human)Chr.Chromosome 20 (human)[1]Band20q13.2Start51,386,957 bp[1]End51,562,831 bp[1...

サイバーパンクからの派生(サイバーパンクからのはせい)では、スペキュレイティブ・フィクションにおけるサイバーパンクからの派生サブジャンルのうち、別個のサブジャンルとして確立していると認識されているものを解説する。これらの派生サブジャンルはサイバーパンクの中心であるコンピュータなどのITの進歩とは関係ないものがほとんどで、サイバーパン...

