QR-—Ä–ĺ–∑–ļ–Ľ–į–ī –ľ–į—ā—Ä–ł—Ü—Ė
|
Read other articles:

Unsolved murders in 19th century London The Thames Torso Murders, often called the Thames Mysteries or the Embankment Murders, were a sequence of unsolved murders of women occurring in London, England from 1887 to 1889. The series included four incidents which were filed as belonging to the same series. None of the cases were solved, and only one of the four victims was identified. In addition, other murders of a similar kind, taking place between 1873 and 1902, have also been associated with...

Untuk kegunaan lain, lihat Messalina (disambiguasi). Valeria MessalinaPermaisuri Kaisar RomawiTahta24 Januari 41 ‚Äď 48Informasi pribadiKelahiran25 Januari 17 atau 20Roma, Kekaisaran RomawiKematian48 (usia 31 atau 28)Taman Lucullus, Roma, Kekaisaran RomawiWangsaJulio-Claudius (dari pernikahan)gens Valeria (dari lahir)AyahMarcus Valerius Messalla BarbatusIbuDomitia Lepida yang MudaPasanganClaudiusAnakClaudia OctaviaTiberius Claudius Caesar Britannicus Messalina menggendong anaknya, Britannicus...

Song by James Blunt MonstersSingle by James Bluntfrom the album Once Upon a Mind Released1 November 2019GenrePopLength4:19LabelAtlantic Records UKSongwriter(s)Blunt, Amy Wadge and Jimmy HogarthJames Blunt singles chronology I Told You (2019) Monsters (2019) Halfway (2020) Music videoMonsters on YouTube Monsters is a song by English singer-songwriter James Blunt. It was written by Blunt, Amy Wadge and Jimmy Hogarth for Blunt's sixth studio album, Once Upon a Mind (2019).[1] It was rele...

Questa voce sull'argomento cestisti statunitensi è solo un abbozzo. Contribuisci a migliorarla secondo le convenzioni di Wikipedia. Segui i suggerimenti del progetto di riferimento. Darnell Harris Nazionalità Stati Uniti Altezza 203 cm Peso 105 kg Pallacanestro Ruolo Ala grande Termine carriera 2020 Carriera Giovanili Alexander Hamilton High School2012-2013University of Wisconsin-Whitewater2013-2014Northwest Florida State College2014-2016 M.T. Blue Raiders Squadre di club 2...

2004 studio album by Lena PhilipssonDet gör ont en stund på natten men inget på danStudio album by Lena PhilipssonReleasedAugust 4, 2004Recorded2004GenrePopLabelColumbiaLena Philipsson chronology Bästa vänner(1997) Det gör ont en stund på natten men inget på dan(2004) Jag ångrar ingenting(2005) Singles from Det gör ont en stund på natten men inget på dan Det gör ontReleased: 17 March 2004 DeliriumReleased: 7 July 2004 Lena AnthemReleased: 11 October 2004 På gatan där j...

Subsequent to the Native American mascot controversy Part of a series onDiscrimination Forms Institutional Structural Attributes Age Caste Class Dialect Disability Genetic Hair texture Height Language Looks Mental disorder Race / Ethnicity Skin color Scientific racism Rank Sex Sexual orientation Species Size Viewpoint Social Arophobia Acephobia Adultism Anti-albinism Anti-autism Anti-homelessness Anti-drug addicts Anti-intellectualism Anti-intersex Anti-left handedness Anti-Masonry A...

Voce principale: Sportgemeinschaft 09 Wattenscheid. Sportgemeinschaft 09 WattenscheidStagione 1974-1975Sport calcio Squadra Wattenscheid 09 Allenatore Karlheinz Feldkamp 2. Bundesliga7¬ļ posto Coppa di GermaniaPrimo turno Maggiori presenzeCampionato: Jendrossek, Klee, Klimke (38)Totale: Klee, Klimke (39) Miglior marcatoreCampionato: Jendrossek (16)Totale: Jendrossek (16) StadioLohrheidestadion Maggior numero di spettatori12 000 vs. Borussia Dortmund Minor numero di spettatori1 ...

This article was written in February 2010 and has only been partially updated since then, most recently in December 2013. Please feel free to further update it Water supply and sanitation in TanzaniaThe flag of TanzaniaDataWater coverage (broad definition)(improved water source) 52% (2007, household survey),[1] 50% ('at least basic' definition,2017, JMP)[2]Sanitation coverage (broad definition)(improved sanitation) 33% (2006, household survey),[1] 24% ('at least basic'...
2020ŚĻīŚ§ŹŚ≠£Ś••śěóŚĆĻŚÖčŤŅźŚä®šľöś≥ĘŚÖįšĽ£Ť°®Śúėś≥ĘŚÖįŚõĹśóóIOCÁ∑®ÁĘľPOLNOCś≥ĘŤė≠Ś•ßśěóŚĆĻŚÖčŚßĒŚď°śúÉÁ∂≤Áęôolimpijski.plÔľąŤčĪśĖáÔľČÔľąś≥ĘŚÖįśĖáÔľČ2020ŚĻīŚ§ŹŚ≠£Ś••śěóŚĆĻŚÖčŤŅźŚä®šľöÔľąśĚĪšļ¨ÔľČ2021ŚĻī7śúą23śó•Ťá≥8śúą8śó•ÔľąŚŹó2019ŚÜ†Áä∂ÁóÖśĮíÁóÖÁĖęśÉÖŚĹĪŚďćśé®ŤŅüԾƚĹÜšĽćšŅĚÁēôŚéüŚģöŚźćÁßįԾȝĀčŚčēŚď°206ŚŹÉŤ≥Ĺť†ÖÁõģ24šł™Ś§ßť°ĻśóóśČ茾ČĻēŚľŹÔľöŚłēÁĽīŚįĒ¬∑ÁßĎÁÉ≠ŚįľŚ••Ś§ęśĖĮŚüļÔľąśłłś≥≥ԾȌíĆť©¨Ś®Ö¬∑ś≤ÉšĽÄšĻĒŚ§ęśĖĮŚć°ÔľąŤá™Ť°ĆŤĹ¶ÔľČ[1]ťó≠ŚĻēŚľŹÔľöŚć°ÁĹóŚą©Ś®ú¬∑Áļ≥šļöÔľąÁöģŚąíŤČáÔľČ&#...

Musei CapitoliniIl complesso dei Musei Capitolini in piazza del Campidoglio: a sinistra Palazzo dei Conservatori, a destra Palazzo Nuovo. UbicazioneStato Italia Localit√†Roma IndirizzoPiazza del Campidoglio, 1 Coordinate41¬į53‚Ä≤35‚Ä≥N 12¬į28‚Ä≤58‚Ä≥E / 41.893056¬įN 12.482778¬įE41.893056; 12.482778Coordinate: 41¬į53‚Ä≤35‚Ä≥N 12¬į28‚Ä≤58‚Ä≥E / 41.893056¬įN 12.482778¬įE41.893056; 12.482778 CaratteristicheTipoArte romana, medievale, rinascimentale e barocca I...

Anatoly Kulikov–ź–Ĺ–į—ā–ĺ–Ľ–ł–Ļ –ö—É–Ľ–ł–ļ–ĺ–≤Kulikov in 2018Minister of Internal AffairsIn office6 July 1995 ‚Äď 23 March 1998PresidentBoris YeltsinPrime MinisterViktor ChernomyrdinPreceded byViktor YerinSucceeded bySergei Stepashin Personal detailsBorn (1946-09-04) September 4, 1946 (age 77)Aigursky, Stavropol Krai, RSFSR, USSRMilitary serviceAllegiance Soviet Union RussiaBranch/serviceSoviet Internal TroopsRussian Internal troopsYears of service1966-1998RankGen...

The list of Roman hoards in Britain comprises significant archaeological hoards of coins, jewellery, precious and scrap metal objects and other valuable items discovered in Great Britain (England, Scotland and Wales) that are associated with period of Romano-British culture when Southern Britain was under the control of the Roman Empire, from AD 43 until about 410, as well as the subsequent Sub-Roman period up to the establishment of Anglo-Saxon kingdoms. It includes both hoards that were bu...
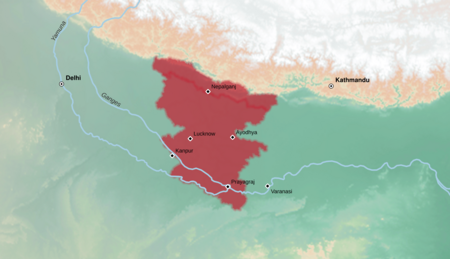
Indo-Aryan language AwadhiAvadhńęŗ§Öŗ§Ķŗ§ßŗ•Ä ¬∑ ūĎāÉūĎāęūĎā°ūĎā≤The word Awadhi written in Devanagari scriptPronunciation[…ô č.dŐ™ Īi]Native toIndia and NepalRegionAwadhEthnicityAwadhisNative speakers38.5 million in India (2011)[1][2][3]500,000 in Nepal (2011)[citation needed]Language familyIndo-European Indo-IranianIndo-AryanCentral Indo-AryanEast CentralAwadhiEarly formsArdhamagadhi Prakrit Ardhamagadhi ApabhraŠĻÉŇõa Dialects Pardesi Gangap...
„ÄĆťļ¶ŚÖčÁĪ≥šľ¶„ÄćťáćŚģöŚźĎŤá≥ś≠§„ÄāŚÖ≥šļéŚÖ∂šĽĖÁĒ®ś≥ēԾƍĮ∑ŤßĀ„ÄĆťļ¶ŚÖčÁĪ≥šľ¶ (ś∂ąś≠ßšĻČ)„Äć„Äā ŚďąÁĹóŚĺ∑¬∑ťļ¶ŚÖčÁĪ≥šľ¶ ťĖ£šłčThe Rt Hon. Harold MacmillanŤĀĒŚźąÁéčŚõĹť¶ĖÁõłšĽĽśúü1957ŚĻī1śúą10śó•‚ÄĒ1963ŚĻī10śúą19śó•ŚźõšłĽšľäšłĹŤééÁôĹšļĆšłĖŚČ暼ĽŚģČśĚĪŚįľ¬∑ŤČĺÁôĽÁĽßšĽĽšļěś≠∑ŚÖč¬∑ťĀľśčČśĖĮ-šľĎŚßÜŤ≤°śĒŅŚ§ßŤá£šĽĽśúü1955ŚĻī12śúą20śó•‚ÄĒ1957ŚĻī1śúą13śó•śÄĽÁźÜŚģČšłúŚįľ¬∑ŤČĺÁôĽŚČ暼ĽśčČŚćö¬∑Ś∑īÁČĻŚčíÁĽßšĽĽŚĹľŚĺó¬∑ťúćŚįľśąąŚ§ęŚ§Ėšļ§Ś§ßŤá£šĽĽśúü1955ŚĻī4śúą7śó•‚ÄĒ1955ŚĻī12śúą20śó•śÄĽÁźÜÔŅĹ...

ŔäŔĀō™ŔāōĪ ŔÖō≠ō™ŔąŔČ ŔáōįŔá ōßŔĄŔÖŔāōßŔĄō© ō•ŔĄŔČ ōßŔĄōßō≥ō™ōīŔáōßōĮ ō®ŔÖōĶōßōĮōĪ. ŔĀō∂ŔĄōßŔčōĆ ō≥ōßŔáŔÖ ŔĀŔä ō™ō∑ŔąŔäōĪ ŔáōįŔá ōßŔĄŔÖŔāōßŔĄō© ŔÖŔÜ ōģŔĄōßŔĄ ō•ō∂ōßŔĀō© ŔÖōĶōßōĮōĪ ŔÖŔąōęŔąŔā ō®Ŕáōß. ō£Ŕä ŔÖōĻŔĄŔąŔÖōßō™ ōļŔäōĪ ŔÖŔąōęŔāō© ŔäŔÖŔÉŔÜ ōßŔĄō™ōīŔÉŔäŔÉ ō®Ŕáōß Ŕąō•ō≤ōßŔĄō™Ŕáōß. (ōĮŔäō≥ŔÖō®ōĪ 2018) ŔĄŔąŔÉŔáŔäōĮ ŔÖōßōĪō™ŔÜ ōĮŔäō≤ōĪō™ ŔáŔąŔÉŔÖōĻŔĄŔąŔÖōßō™ ōĻōßŔÖō©ō®ŔĄōĮ ōßŔĄō£ōĶŔĄ ōßŔĄŔąŔĄōßŔäōßō™ ōßŔĄŔÖō™ō≠ōĮō©ōßŔĄō™ō∑ŔąŔäōĪ ŔąōßŔĄō™ōĶŔÜŔäōĻōßŔĄōĶōßŔÜōĻ ŔĄŔąŔÉŔáŔäōĮō™ōĻōĮŔäŔĄ - ō™ōĻōĮŔäÔŅĹ...

ō≠Ŕźō≥ŔíŔÖŔéŔČ ŔÖŔąŔāōĻ ō™ŔāōĪŔäō®Ŕä ŔĄōĶō≠ōĪōßō° ō≠ō≥ŔÖŔČ ōßŔĄŔÖŔąŔāōĻ ōßŔĄō®ŔĄōĮ ōßŔĄō£ōĪōĮŔÜ ōßŔĄō≥ōĻŔąōĮŔäō© ōßŔĄō•ō≠ōĮōßōęŔäōßō™ 29¬į16‚Ä≤43‚Ä≥N 35¬į28‚Ä≤54‚Ä≥E / 29.278635¬įN 35.481684¬įE / 29.278635; 35.481684 ōßŔĄōßōĪō™ŔĀōßōĻōßō™ ō®ŔäōßŔÜōßō™ ō£ōģōĪŔČ ōßŔĄō£ŔÖō∑ōßōĪ ŔÖōß ō®ŔäŔÜ 50-100 ŔÖŔĄŔÖ. ōßŔĄŔÖŔąōßōĪōĮ ōßŔĄō∑ō®ŔäōĻŔäō© ŔÖŔäōßŔá ō¨ŔąŔĀŔäō© ōßŔĄŔÖōĻōßŔĄŔÖ ŔąōßōĮŔä ōĪŔÖ Ŕąō¨ō®ŔĄ ōßŔĄŔĄŔąō≤ ō™ōĻōĮŔäŔĄ ŔÖōĶōĮōĪŔä - ō™ōĻōĮŔäŔĄ ōĶō≠ōĪōßō° ō≠Ŕźō≥ŔíŔÖŔéŔČ ÔŅĹ...

–í –í–ł–ļ–ł–Ņ–Ķ–ī–ł–ł –Ķ—Ā—ā—Ć —Ā—ā–į—ā—Ć–ł –ĺ –ī—Ä—É–≥–ł—Ö –Ľ—é–ī—Ź—Ö —Ā —ā–į–ļ–ĺ–Ļ —Ą–į–ľ–ł–Ľ–ł–Ķ–Ļ, —Ā–ľ. –ē—Ä–≥–ĺ–ľ—č—ą–Ķ–≤. –ö–ĺ–Ĺ—Ā—ā–į–Ĺ—ā–ł–Ĺ –õ—Ć–≤–ĺ–≤–ł—á –ē—Ä–≥–ĺ–ľ—č—ą–Ķ–≤ –ú–ł—á–ľ–į–Ĺ –ö. –õ. –ē—Ä–≥–ĺ–ľ—č—ą–Ķ–≤ –Ē–į—ā–į —Ä–ĺ–∂–ī–Ķ–Ĺ–ł—Ź 20 –į–Ņ—Ä–Ķ–Ľ—Ź 1856(1856-04-20) –Ē–į—ā–į —Ā–ľ–Ķ—Ä—ā–ł 1916(1916) –†–ĺ–ī –ī–Ķ—Ź—ā–Ķ–Ľ—Ć–Ĺ–ĺ—Ā—ā–ł –ĺ—Ą–ł—Ü–Ķ—Ä –ü—Ä–ł–Ĺ–į–ī–Ľ–Ķ–∂–Ĺ–ĺ—Ā—ā—Ć –†–ĺ—Ā—Ā–ł—Ź –†–ĺ–ī –≤–ĺ–Ļ—Ā–ļ –í–ú–§ –ď–ĺ–ī—č —Ā–Ľ—É–∂–Ī—č 1875-1914 –ó–≤–į–Ĺ–ł–Ķ –ď–Ķ–Ĺ–Ķ—Ä–į–Ľ...

King of Assyria Adad-nńęrńĀrńę IIIKing of AssyriaKing of the UniverseThe Tell al-Rimah Stele was discovered in 1967 and commemorates Adad-nirari III‚Äôs campaigns in the West.[1]King of the Neo-Assyrian EmpireReign811‚Äď783 BCPredecessorShamshi-Adad VSuccessorShalmaneser IVIssueAshur-nirari V Shalmaneser IV Ashur-dan IIITiglath-Pileser III?FatherShamshi-Adad VMotherShammuramat Adad-nńęrńĀrńę III (also Adad-nńĀrńĀrńę, meaning Adad (the storm god) is my help) was a King of Assyria from ...

Aeroporto di Dobbiacoaeroporto Codice IATAnessuno Codice ICAOLIVD DescrizioneTipoMilitare GestoreAeronautica Militare Stato Italia Regione Trentino-Alto Adige PosizioneDobbiaco Costruzione1915 - 1966 Altitudine1 239,9264 m s.l.m. Coordinate46¬į43‚Ä≤34‚Ä≥N 12¬į13‚Ä≤32‚Ä≥E46¬į43‚Ä≤34‚Ä≥N, 12¬į13‚Ä≤32‚Ä≥E Mappa di localizzazioneLIVD PisteOrientamento (QFU)LunghezzaSuperficie10-28980erba Modifica dati su Wikidata ¬∑ Manuale L'aeroporto di Dobbiaco (in tedesco Flu...

SMAN 3 TasikmalayaSekolah Menengah Atas Negeri 3 TasikmalayaInformasiJenisNegeriAkreditasiANomor Pokok Sekolah Nasional20224509Kepala SekolahDra. Elin Yuliani, M.Pd.Jurusan atau peminatanMIPA, IPS dan Bahasa dan BudayaKurikulumKurikulum 2013AlamatLokasiJl. Letkol Basir Surya No. 89, Sukanagara, Kec. Purbaratu, Tasikmalaya, Jawa Barat, IndonesiaTel./Faks.+62 265 334889Koordinat7¬į20‚Ä≤30‚Ä≥S 108¬į15‚Ä≤04‚Ä≥E / 7.341582¬įS 108.251175¬įE / -7.341582; 108.251175Situs&...


![{\displaystyle A=[\mathbf {a} _{1},\cdots ,\mathbf {a} _{n}]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/6824116d015e9599acde43bcfe0bfc286f331c92)








![{\displaystyle Q=\left[\mathbf {e} _{1},\cdots ,\mathbf {e} _{n}\right]\qquad {\text{and}}\qquad R={\begin{pmatrix}\langle \mathbf {e} _{1},\mathbf {a} _{1}\rangle &\langle \mathbf {e} _{1},\mathbf {a} _{2}\rangle &\langle \mathbf {e} _{1},\mathbf {a} _{3}\rangle &\ldots \\0&\langle \mathbf {e} _{2},\mathbf {a} _{2}\rangle &\langle \mathbf {e} _{2},\mathbf {a} _{3}\rangle &\ldots \\0&0&\langle \mathbf {e} _{3},\mathbf {a} _{3}\rangle &\ldots \\\vdots &\vdots &\vdots &\ddots \end{pmatrix}}.}](https://wikimedia.org/api/rest_v1/media/math/render/svg/f6c03b414c06cbc293519a41cfcab0ca4084171c)


















































