Ґратка E8
|
Read other articles:

Hubungan Timor Leste–Spanyol Timor Leste Spanyol Hubungan Timor Leste dengan Spanyol adalah hubungan bilateral dan diplomatik antara kedua negara tersebut. Timor Leste tidak memiliki kedutaan besar di Spanyol tetapi kedutaan besarnya di Lisbon diakreditasi untuk negara Spanyol.[1] Spanyol juga tidak memiliki kedutaan besar di Timor Leste, menjalankan fungsi diplomatiknya dengan Timor Leste melalui kedutaan besarnya di Jakarta, Indonesia.[2] Lihat pula Hubungan luar negeri T...
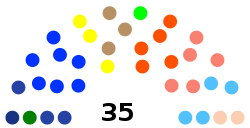
Dewan Perwakilan Rakyat Kabupaten Aceh Besar DPRK Aceh Besar2019-2024JenisJenisUnikameral Jangka waktu5 tahunSejarahSesi baru dimulai20 Agustus 2019PimpinanKetuaIskandar Ali, S.Pd., M.Si. (PAN) sejak 20 September 2019 Wakil Ketua IBakhtiar, S.T., M.Si. (PA) sejak 20 September 2019 Wakil Ketua IIZulfikar Aziz, S.E. (PKS) sejak 20 September 2019 KomposisiAnggota35Partai & kursi NasDem (1) PKB (1) Demokrat (3) PAN (7) Gol...

العلاقات السودانية الكرواتية السودان كرواتيا السودان كرواتيا تعديل مصدري - تعديل العلاقات السودانية الكرواتية هي العلاقات الثنائية التي تجمع بين السودان وكرواتيا.[1][2][3][4][5] مقارنة بين البلدين هذه مقارنة عامة ومرجعية للدولتين: وجه ال...

Gregory PeckPeck pada tahun 1948LahirEldred Gregory Peck(1916-04-05)5 April 1916La Jolla, California, U.S.Meninggal12 Juni 2003(2003-06-12) (umur 87)Los Angeles, California, U.S.AlmamaterUniversity of California, BerkeleyPekerjaanActorTahun aktif1942–2000Suami/istri Greta Kukkonen (m. 1942; c. 1955) Veronique Passani (m. 1955) Anak5, di antaranya Cecilia PeckKeluargaEthan Peck (cucu)PenghargaanAcad...

This article's lead section may be too short to adequately summarize the key points. Please consider expanding the lead to provide an accessible overview of all important aspects of the article. (September 2021) Town in Ontario, CanadaCollingwoodTown (lower-tier)Town of CollingwoodDowntown Collingwood LogoNicknames: C-wood, The WoodCollingwoodShow map of Simcoe CountyCollingwoodShow map of Southern OntarioCoordinates: 44°30′N 80°13′W / 44.500°N 80.217°W / ...

Amuntai SelatanKecamatanKantor kecamatan Amuntai SelatanPeta lokasi Kecamatan Amuntai SelatanNegara IndonesiaProvinsiKalimantan SelatanKabupatenHulu Sungai UtaraPemerintahan • Camat...Populasi • Total... jiwa jiwaKode Kemendagri63.08.04 Kode BPS6308040 Luas... km² Amuntai Selatan adalah sebuah kecamatan di Kabupaten Hulu Sungai Utara, Provinsi Kalimantan Selatan, Indonesia. Galeri Tugu Perjuangan di Telaga Silaba. lbsKecamatan Amuntai Selatan, Kabupaten Hulu Sung...

Die Artikel Geschichte der Juden #Antisemitismus und Geschichte des Antisemitismus bis 1945 überschneiden sich thematisch. Informationen, die du hier suchst, können sich also auch im anderen Artikel befinden.Gerne kannst du dich an der betreffenden Redundanzdiskussion beteiligen oder direkt dabei helfen, die Artikel zusammenzuführen oder besser voneinander abzugrenzen (→ Anleitung). Karikatur auf der Titelseite von Édouard Drumonts antisemitischer Zeitschrift La Libre Parole ...

« Joyau » redirige ici. Pour les autres significations, voir Joyaux. Si ce bandeau n'est plus pertinent, retirez-le. Cliquez ici pour en savoir plus. Cet article ne cite pas suffisamment ses sources (novembre 2009). Si vous disposez d'ouvrages ou d'articles de référence ou si vous connaissez des sites web de qualité traitant du thème abordé ici, merci de compléter l'article en donnant les références utiles à sa vérifiabilité et en les liant à la section « Notes ...

War between United States and the Barbary states, 1801–1805 First Barbary WarPart of the Barbary WarsUSS Enterprise fighting the Tripolitan polacca Tripoli by William Bainbridge Hoff, 1878DateMay 10, 1801 – June 10, 1805(4 years and 1 month)LocationOff the Mediterranean coast of Tripoli; DernaResult Peace treaty The United States paying ransom Tripolitania ships allowed to inspect American ships Freeing prisoners of American shipsBelligerents United States Sweden (18...

この記事は検証可能な参考文献や出典が全く示されていないか、不十分です。出典を追加して記事の信頼性向上にご協力ください。(このテンプレートの使い方)出典検索?: コルク – ニュース · 書籍 · スカラー · CiNii · J-STAGE · NDL · dlib.jp · ジャパンサーチ · TWL(2017年4月) コルクを打ち抜いて作った瓶の栓 コルク(木栓、�...

Juana EnríquezRatu Aragon, Mallorca, Valencia, Navarra dan Sisilia; Comtesse BarcelonaPermaisuri AragonPeriode7 Juni 1458 – 13 Februari 1468Informasi pribadiKelahiran1425TorrelobatónKematian13 Februari 1468 – 1425; umur -44–-43 tahunTarragonaPemakamanBiara PobletWangsaEnríquezAyahFadrique Enríquez de MendozaIbuMariana Fernández de CórdobaPasanganJuan II dari AragónAnakFerrando II d'AragónJuana, Ratu NapoliAgamaKatolik Roma Juana Enriquez de Cordoba, Lady ke-5 Casarr...

这是马来族人名,“阿末”是父名,不是姓氏,提及此人时应以其自身的名“祖基菲里”为主。 尊敬的拿督斯里哈芝祖基菲里·阿末Dzulkefly bin Ahmad国会议员、DGSM博士 马来西亚卫生部部长现任就任日期2023年12月12日君主最高元首苏丹阿都拉最高元首苏丹依布拉欣·依斯迈首相安华·依布拉欣副职卡尼斯曼(英语:Lukanisman Awang Sauni)前任扎丽哈·慕斯达法任期2018年5月21日—2...

此條目可参照英語維基百科相應條目来扩充。 (2021年5月6日)若您熟悉来源语言和主题,请协助参考外语维基百科扩充条目。请勿直接提交机械翻译,也不要翻译不可靠、低品质内容。依版权协议,译文需在编辑摘要注明来源,或于讨论页顶部标记{{Translated page}}标签。 约翰斯顿环礁Kalama Atoll 美國本土外小島嶼 Johnston Atoll 旗幟颂歌:《星條旗》The Star-Spangled Banner約翰斯頓環礁�...

Artikel ini sebatang kara, artinya tidak ada artikel lain yang memiliki pranala balik ke halaman ini.Bantulah menambah pranala ke artikel ini dari artikel yang berhubungan atau coba peralatan pencari pranala.Tag ini diberikan pada Januari 2023. Sekolah Menengah Maotanchang Anhui Lu'An (毛坦厂中学) merupakan sekolah menengah di Kecamatan Maotanchang, Kota Maotanchang, Distrik Jin'an, Lu'an, Anhui, Tiongkok. Sekolah ini dikenal sebagai 'Pabrik Gaokao' terbesar dan terkenal dengan model ind...

Football stadium in Leicester, England King Power StadiumUEFA Full nameKing Power StadiumFormer namesWalkers Stadium (2002–2011)LocationFilbert WayLeicesterLE2 7FLPublic transit LeicesterOwnerKing PowerCapacity32,261 [1]Record attendanceFootball: 32,241 (Leicester City vs Sunderland, 8 August 2015) Rugby: 32,500 (Leicester Tigers vs Bath, 1 April 2006)Field size105 by 68 metres (114.8 yd × 74.4 yd)[1]SurfaceDesso GrassMasterConstructionBroke ground2000Built20...

Oli PettigrewLahir2 April 1981 (umur 43)Hong KongPekerjaanAktor, model, dan pembawa acara televisiTahun aktif1999 - sekarangSitus webhttp://www.olipettigrew.com/ Oliver Pettigrew (lahir 2 April 1981) adalah seorang aktor Inggris kelahiran Hong Kong, model, dan pembawa acara televisi, dan sekarang berbasis di Singapura. Dia dikenal membawakan acara Cybermax dan Technomax di kanal Animax dan Sony Style di AXN.[1] Dia memiliki gelar BA(Hons) dalam Komunikasi Korporasi. Dia men...

Die Estnische Apostolische Orthodoxe Kirche (estnisch Eesti Apostlik-Õigeusu Kirik, kurz: EAÕK/deutsch EAOK) ist eine orthodoxe Kirche in Estland. Sie untersteht dem Ökumenischen Patriarchat von Konstantinopel als autonome Kirche. Sie ist nicht identisch mit der Estnisch-Orthodoxen Kirche des Moskauer Patriarchats (estnisch Moskva Patriarhaadi Eesti Õigeusu Kirik, kurz: MPEÕK). Inhaltsverzeichnis 1 Geschichte 2 Aktuelle Situation 3 Literatur 4 Weblinks 5 Einzelnachweise Geschichte Im sei...

Narrowband radio signal detected in April and May 2019 Parkes Observatory that detected BLC-1 BLC1 (Breakthrough Listen Candidate 1) was a candidate SETI radio signal detected and observed during April and May 2019, and first reported on 18 December 2020, spatially coincident with the direction of the Solar System's closest star, Proxima Centauri.[1][2][3] Signal The apparent shift in its frequency, consistent with the Doppler effect, was suggested to be inconsistent w...

American microbiologist For people with similar names, see Daniel Nathan. Daniel NathansBorn(1928-10-30)October 30, 1928Wilmington, DelawareDiedNovember 16, 1999(1999-11-16) (aged 71)Baltimore, MarylandNationalityAmericanEducationUniversity of Delaware (BS)Washington University in St. Louis (MD)Known forRestriction enzymesSpouseJoanne GombergAwardsNAS Award in Molecular Biology (1976)Nobel Prize in Physiology or Medicine (1978)National Medal of Science (1993)Scientific careerFieldsM...

Pre-Christian mythology of Ireland This article has multiple issues. Please help improve it or discuss these issues on the talk page. (Learn how and when to remove these template messages) This article includes a list of general references, but it lacks sufficient corresponding inline citations. Please help to improve this article by introducing more precise citations. (April 2009) (Learn how and when to remove this message) This article needs additional citations for verification. Please hel...









![{\displaystyle \left[{\begin{smallmatrix}2&-1&0&0&0&0&0&1/2\\0&1&-1&0&0&0&0&1/2\\0&0&1&-1&0&0&0&1/2\\0&0&0&1&-1&0&0&1/2\\0&0&0&0&1&-1&0&1/2\\0&0&0&0&0&1&-1&1/2\\0&0&0&0&0&0&1&1/2\\0&0&0&0&0&0&0&1/2\end{smallmatrix}}\right].}](https://wikimedia.org/api/rest_v1/media/math/render/svg/fcefbdf5aee18d0241cc76e27b03eaba84feecb4)




![{\displaystyle H_{4}={\tfrac {1}{2}}\left[{\begin{smallmatrix}1&1&1&1\\1&-1&1&-1\\1&1&-1&-1\\1&-1&-1&1\\\end{smallmatrix}}\right].}](https://wikimedia.org/api/rest_v1/media/math/render/svg/d82009a306ed4402cbc4d29bb36011d9e86e2212)





















