Шепс

Шепс
Schöps
—  громада  —
Вид Шепс
Вид Шепс
Герб Шепс
Герб
Координати: 50°50′5″ пн. ш. 11°35′52″ сх. д. / 50.83472° пн. ш. 11.59778° сх. д. / 50.83472; 11.59778
Країна Німеччина Німеччина
Земля Тюрингія
Район Заале-Гольцланд
Об'єднання громад Зюдліхес-Заалеталь
Площа
 - Повна 4,35 км²
Висота над р.м. 158 м 
Населення (31 грудня 2021[1])
 - Усього 244
 - Густота 56,1/км²
Часовий пояс CET (UTC+1)
 - Літній час CEST (UTC+2)
Поштовий код 07768
Телефонний код(и) 036424
Ідентифікаційний код 16 0 74 087
Вебсайт: www.vg-suedliches-saaletal.de
Розташування Шепс
Шепс на карті району
Шепс на карті району
Шепс. Карта розташування: Німеччина
Шепс
Шепс
Розташування на карті Німеччини
Мапа

Шепс (нім. Schöps) — громада в Німеччині, розташована в землі Тюрингія. Входить до складу району Заале-Гольцланд. Складова частина об'єднання громад Зюдліхес-Заалеталь.

Площа — 4,35 км2. Населення становить 244 ос. (станом на 31 грудня 2021).

Галерея

Примітки

  1. ↑ Bevölkerung der Gemeinden vom Thüringer Landesamt für Statistik (нім.)

Посилання

Вікісховище має мультимедійні дані за темою: Шепс

Німеччина Це незавершена стаття з географії Німеччини.
Ви можете допомогти проєкту, виправивши або дописавши її.

Read other articles:

Gempa bumi Turki–Suriah 2023

Gempa bumi Turki–Suriah 2023Searah jarum jam dari atas: Bangunan runtuh di Provinsi Hatay, pemandangan reruntuhan dari Aleppo, Suriah, Langit Biru China dan tim SAR Iran di Adıyaman, bantuan USAID di Pangkalan Udara İncirlik dan kota tenda di KahramanmaraşIstanbulAnkaraAleppoM7.8M7.5Tampilkan peta TurkeyAleppoM7.8M7.5Tampilkan peta SyriaWaktu UTC2023-02-06 01:17:35ISC625613033USGS-ANSSComCat ComCatTanggal setempat6 Februari 2023 (2023-02-06)Waktu setempat04:17 TR...

 

Keuskupan Mbulu

Keuskupan MbuluDioecesis MbuluensisLokasiNegaraTanzaniaMetropolitArushaStatistikLuas16.057 km2 (6.200 sq mi)Populasi- Total- Katolik(per 2004)924.462242,698 (26.3%)InformasiRitusRitus LatinKepemimpinan kiniPausFransiskusUskupBeatus Kinyaiya Keuskupan Mbulu (Latin: Dioecesis Mbuluensiscode: la is deprecated ) adalah sebuah keuskupan yang terletak di kota Mbulu, provinsi gerejawi Arusha, Tanzania. Tahta Uskupnya adalah Gereja Katedral Bunda Maria. Riwayat 14 A...

 

Abiy Ahmed

Prime Minister of Ethiopia since 2018 Abiy redirects here. For the town, see Abiy Addi. In this Ethiopian name, the name Ahmed Ali is a patronymic, and the person should be referred by the given name, Abiy. This article may require cleanup to meet Wikipedia's quality standards. The specific problem is: Excessive quotes from sources in citations. Please help improve this article if you can. (March 2024) (Learn how and when to remove this template message) Abiy Ahmedአቢይ አሕመድAbiy i...

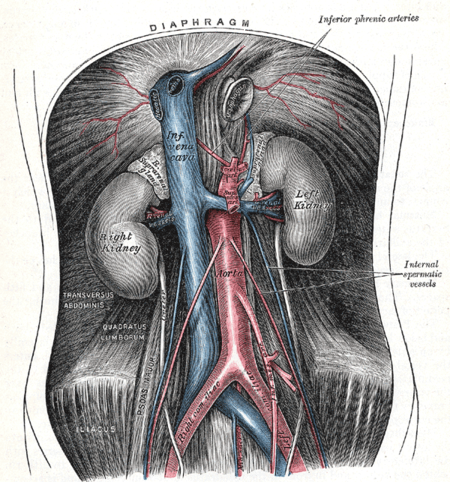
Gonadal artery

This article relies largely or entirely on a single source. Relevant discussion may be found on the talk page. Please help improve this article by introducing citations to additional sources.Find sources: Gonadal artery – news · newspapers · books · scholar · JSTOR (February 2024) Gonadal arteryThe abdominal aorta and its branches.DetailsSourceabdominal aortaVeingonadal veinSuppliesgonadsAnatomical terminology[edit on Wikidata] The term gonadal art...

 

Mingyi Swa

For other people named Mingyi Swa, see Mingyi Swa (disambiguation). Heir Apparent of Burma Mingyi Swa မင်းကြီးစွာHeir Apparent of BurmaReign15 October 1581 – 8 January [O.S. 29 December 1592] 1593PredecessorNandaSuccessorMinye Kyawswa IIBorn27 November 1558 Sunday, 2nd waning of Nadaw 920 MEPegu (Bago), Toungoo EmpireDied8 January [O.S. 29 December 1592] 1593 (aged 34) Friday, 8th waxing of Tabodwe 954 MESuphan Buri, SiamBurialFebrua...

 

Piala Liga Inggris 1993–1994

Piala Liga Inggris 1993–19941993–94 Football League CupNegara Inggris WalesTanggal penyelenggaraan16 Agustus 1993 s.d. 27 Maret 1994Jumlah peserta92Juara bertahanArsenalJuaraAston Villa(gelar ke-4)Tempat keduaManchester UnitedPencetak gol terbanyakDalian AtkinsonIan Wright(6 gol)← 1992–1993 1994–1995 → Piala Liga Inggris 1993–1994 adalah edisi ke-34 penyelenggaraan Piala Liga Inggris, sebuah kompetisi dengan sistem gugur untuk 92 tim terbaik di Inggris. Edisi ini dimen...

Akbarieh Garden

The Akbarieh Garden and Mansion Akbarieh Garden is a UNESCO World Heritage Site in Birjand, South Khorasan Province, Iran (WHS 1372–009).[1] It was inscribed on the UNESCO World Heritage List in 2011. It annually receives thousands of domestic and foreign tourists. It is concomitantly used as a museum and tourist space.[2] History The Akbarieh Garden was built in the Qajar era by Heshmat ol-Molk I, the governor of Qohestan and Sistan in 1880. As with most gardens in history,...

 

Gopalkrishna Gandhi

Gopalkrishna Gandhi Gubernur Bengal Barat ke-23Masa jabatan14 Desember 2004 – 14 Desember 2009PendahuluViren J. ShahPenggantiDevanand KonwarGubernur Bihar ke-21Masa jabatan31 Januari 2006 – 21 Juni 2006PendahuluButa SinghPenggantiR. S. Gavai Informasi pribadiLahirGopalkrishna Devdas Gandhi22 April 1945 (umur 79)Delhi, India BritaniaPartai politikIndependenAfiliasi politiklainnyaAliansi Progresif BersatuSuami/istriTara GandhiAnak2 putriOrang tuaDevdas GandhiLakshmi G...

 

Dark current (physics)

This article relies largely or entirely on a single source. Relevant discussion may be found on the talk page. Please help improve this article by introducing citations to additional sources.Find sources: Dark current physics – news · newspapers · books · scholar · JSTOR (January 2024) Weak electric current generated by photosensitive devices in pure darknessIn physics and in electronic engineering, dark current is the relatively small electric cu...

Albertus Magnus

German Dominican friar and saint (c. 1200–1280) Albertus redirects here. For other uses, see Albertus (disambiguation). Albert the Great redirects here. For the American Thoroughbred racehorse, see Albert the Great (horse). For the asteroid, see 20006 Albertus Magnus. SaintAlbertus MagnusOPThe Apparition of the Virgin to Saint Albert the Great by Vicente Salvador GomezBishop of RegensburgDoctor of the ChurchBornc. 1200[1]Lauingen, Duchy of BavariaDied15 November 1280Cologne, H...

 

若望保祿二世

本條目存在以下問題，請協助改善本條目或在討論頁針對議題發表看法。 此條目需要补充更多来源。 (2017年12月19日)请协助補充多方面可靠来源以改善这篇条目，无法查证的内容可能會因為异议提出而被移除。致使用者：请搜索一下条目的标题（来源搜索：若望保祿二世 — 网页、新闻、书籍、学术、图像），以检查网络上是否存在该主题的更多可靠来源（判定指引）。 �...

 

Razia Sultan (seri televisi)

Razia SultanKartu LogoGenreDrama sejarahPembuatSiddarth Kumar TewaryDitulis olehAnshuman SinhaSurabhi SaralSaba MumtazSutradaraMukesh kumar singh Arif Ali Ansari Hasnain Haiderabadwala Manish Singh Kamal Monga Pengarah kreatifPrakriti MukherjeeAmol SoorveyPresenterSwastik PicturesPemeranPankhuri Awasthy RodeNegara asalIndiaBahasa asliHindiJmlh. musim1Jmlh. episode170ProduksiProduserSiddarth Kumar Tewary Gayatri Gill Tewary Rahul Kumar TewaryLokasi produksiIndiaPenyuntingParesh Shah Ayan B Ha...

國民陣線

国民阵线Barisan NasionalNational Frontباريسن ناسيونلபாரிசான் நேசனல்国民阵线标志简称国阵，BN主席阿末扎希总秘书赞比里署理主席莫哈末哈山总财政希山慕丁副主席魏家祥维纳斯瓦兰佐瑟古律创始人阿都拉萨成立1973年1月1日 (1973-01-01)[1]设立1974年7月1日 (1974-07-01)前身 联盟总部 马来西亚  吉隆坡 50480 秋傑区敦依斯迈路太子世贸中心（英�...

 

Філософія

Частина серії проФілософіяLeft to right: Plato, Kant, Nietzsche, Buddha, Confucius, AverroesПлатонКантНіцшеБуддаКонфуційАверроес Філософи Епістемологи Естетики Етики Логіки Метафізики Соціально-політичні філософи Традиції Аналітична Арістотелівська Африканська Близькосхідна іранська Буддій�...

 

ديه كلارك

هذه المقالة يتيمة إذ تصل إليها مقالات أخرى قليلة جدًا. فضلًا، ساعد بإضافة وصلة إليها في مقالات متعلقة بها. (يوليو 2019) ديه كلارك معلومات شخصية الميلاد 13 يناير 1981 (43 سنة)  غلاسكو  مواطنة المملكة المتحدة  الحياة العملية المدرسة الأم ثانوية هوليرود  [لغات أخرى]‏ ...

أبارتايد

أبارتيدمعلومات عامةصنف فرعي من عزل عنصريفرق تسد البداية 1948 الاختصاص جنوب غرب إفريقياجنوب إفريقيا النص التأسيسي Prohibition of Mixed Marriages Act, 1949 (en) Immorality Act (en) قانون تسجيل السكان لعام 1950 اشتق من سيادة البيضعنصريةسيادة البيض أحداث مهمة Coloured vote constitutional crisis (en) تسبب في Legacies of apartheid (en) ال�...

 

Isocyanate

Chemical group (–N=C=O) Not to be confused with Isocyanide. The isocyanate functional group In organic chemistry, isocyanate is the functional group with the formula R−N=C=O. Organic compounds that contain an isocyanate group are referred to as isocyanates. An organic compound with two isocyanate groups is known as a diisocyanate. Diisocyanates are manufactured for the production of polyurethanes, a class of polymers.[1][2][3] Isocyanates should not be confused wit...

 

James I. Mestrovitch

James I. MestrovitchMedal of Honor recipientBirth nameJoko MeštrovićNickname(s)JackBorn(1894-05-22)May 22, 1894Đuraševići, Austria-Hungary (modern-day Montenegro)DiedNovember 4, 1918(1918-11-04) (aged 24)Fismes, FrancePlace of burialSaint Jovan Serbian Orthodox Church, ĐuraševićiAllegianceUnited States of AmericaService/branchUnited States ArmyYears of service1916–1918RankSergeantService number1243675UnitCompany C, 111th Infantry, 28th DivisionBattles/wars Pancho Villa Exp...

2022 Vermont Senate election

Not to be confused with 2022 United States Senate election in Vermont. 2022 Vermont Senate election ← 2020 November 8, 2022 2024 → All 30 seats in the Vermont Senate16 seats needed for a majority   Majority party Minority party Third party   Leader Becca Balint (retired) Randy Brock Anthony Pollina (retired) Party Democratic Republican Progressive Leader since January 6, 2021 January 6, 2021 2013 Leader's seat Windham Franklin Washington Last el...

 

Bertrand's postulate

Joseph Louis François Bertrand Existence of a prime number between any number and its double In number theory, Bertrand's postulate is the theorem that for any integer n > 3 {\displaystyle n>3} , there exists at least one prime number p {\displaystyle p} with n < p < 2 n − 2. {\displaystyle n<p<2n-2.} A less restrictive formulation is: for every n > 1 {\displaystyle n>1} , there is always at least one prime p {\displaystyle p} such that n < p < 2 n . {\di...