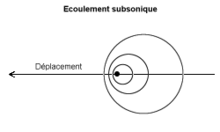
Число Маха
|
Read other articles:

Templat:Korean membutuhkan parameter |hangul=.Lee Soo-man이수만李秀滿Lahir18 Juni 1952 (umur 71)Kebangsaan Korea SelatanPendidikanM.A. in Computer EngineeringAlmamaterCalifornia State University,Seoul National UniversityPekerjaanSinger, Chairman, entrepreneurPenghargaan2008 M.net Golden Disk Award for Record Producer of the Year1997 SBS Seoul Music Award for Record Producer 2011 Seoul Cultural Arts Awards for Pop Music Producer’s Award SM Entertainment 2012 1st Gao...

Austrian Airlines AG IATA ICAO Kode panggil OS AUA AUSTRIAN Didirikan30 September 1957Mulai beroperasi31 Maret 1958PenghubungBandara WinaProgram penumpang setiaMiles & MoreLounge bandaraAustrian Senator Lounge, Austrian Business Lounge & HON CircleAliansiStar AllianceArmada61Tujuan130SloganThe charming way to flyPerusahaan indukLufthansa GroupKantor pusatSchwechat, AustriaTokoh utamaAlexis von Hoensbroech (CEO)Situs webwww.austrian.com Austrian Airlines AG atau sering disebut Austrian...

Loan provided by a group of lenders This article has multiple issues. Please help improve it or discuss these issues on the talk page. (Learn how and when to remove these template messages) This article needs additional citations for verification. Please help improve this article by adding citations to reliable sources. Unsourced material may be challenged and removed.Find sources: Syndicated loan – news · newspapers · books · scholar · JSTOR (February...

College basketball team UTSA Roadrunners 2023–24 UTSA Roadrunners men's basketball team UniversityUniversity of Texas at San AntonioFirst season1981All-time record444–411 (.519)Head coachAustin Claunch (1st season)ConferenceThe AmericanLocationSan Antonio, TexasArenaConvocation Center (Capacity: 2,650)NicknameRoadrunnersColorsNavy blue, orange, and white[1] Uniforms Home Away NCAA tournament appearances1988, 1999, 2004, 2011Conference to...

ليمان سبيتزر معلومات شخصية اسم الولادة (بالإنجليزية: Lyman Strong Spitzer II) الميلاد 26 يونيو 1914 [1] توليدو الوفاة 31 مارس 1997 (82 سنة) [1][2] برينستون مواطنة الولايات المتحدة عضو في الأكاديمية الأمريكية للفنون والعلوم، وفاي بيتا كابا، والجمعية ا...
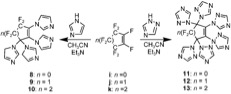
Class of chemical compounds This article relies excessively on references to primary sources. Please improve this article by adding secondary or tertiary sources. Find sources: Perfluorocycloalkene – news · newspapers · books · scholar · JSTOR (January 2024) (Learn how and when to remove this template message) A perfluorocycloalkene (PFCA) fluorocarbon structure with a cycloalkene core. PFCAs have shown reactivity with a wide variety of nucleophiles in...

Kisah Para Rasul 2Kisah Para Rasul 2:11-22 dalam bahasa Yunani pada Uncial 076, yang ditulis sekitar abad ke-5/ke-6.KitabKisah Para RasulKategoriSejarah gerejaBagian Alkitab KristenPerjanjian BaruUrutan dalamKitab Kristen5← pasal 1 pasal 3 → Kisah Para Rasul 2 (disingkat Kis 2) adalah pasal kedua Kitab Kisah Para Rasul dalam Perjanjian Baru di Alkitab Kristen. Ditulis oleh Lukas, seorang Kristen yang merupakan teman seperjalanan Rasul Paulus.[1][2] Teks Naskah asli...

Coppa Libertadores 1998Copa Libertadores de América 1998 Competizione Coppa Libertadores Sport Calcio Edizione 39ª Organizzatore CONMEBOL Date 4 febbraio 1998 - 26 agosto 1998 Partecipanti 23 Risultati Vincitore Vasco da Gama(1º titolo) Secondo Barcelona Statistiche Miglior marcatore Sérgio João (10) Incontri disputati 99 Gol segnati 244 (2,46 per incontro) Cronologia della competizione 1997 1999 Manuale XXXIX Copa Libertadores 1998 Indice 1 Turno preliminare Messico Venezuela...

Charles Taze Russel Bagian dari seriSaksi-Saksi Yehuwa Ikhtisar Struktur organisasi Badan Pimpinan Watch Tower Bibleand Tract Society Badan usaha Sejarah Gerakan Siswa Alkitab Sengketa kepemimpinan Kelompok-kelompok pecahan Perkembangan doktrin Prediksi-prediksi keliru Demografi Menurut negara-negara KepercayaanRitual KeselamatanEskatologi 144.000 Hamba yang setia dan bijaksana HymneNama Tuhan DarahDisiplin Literatur Menara PengawalSadarlah! Kitab Suci Terjemahan Dunia Baru Daftar publikasi D...

Queensland Open 1982 Sport Tennis Data 21 novembre – 28 novembre Edizione 87ª Superficie Erba Campioni Singolare maschile Charles Fancutt Singolare femminile Wendy Turnbull Doppio maschile Dale Collings / Wayne Hampton Doppio femminile Billie Jean King / Anne Smith 1981 1983 Il Queensland Open 1982 è stato un torneo di tennis giocato sull'erba che fa parte del WTA Tour 1982. Il torneo si è giocato a Brisbane in Australia dal 21 al 28 novembre 1982. Indice 1 Campioni 1.1 Singolare maschi...

American college baseball team Monmouth Hawks 2024 Monmouth Hawks baseball teamUniversityMonmouth UniversityHead coachDean Ehehalt (31st season)ConferenceColonial Athletic AssociationLocationWest Long Branch, New JerseyHome stadiumMonmouth Baseball FieldNicknameHawksColorsMidnight blue and white[1] NCAA Tournament appearances1998, 1999, 2007, 2009Conference tournament championsNEC: 1998, 1999, 2007, 2009Regular season conference championsNEC: 1989, 1991, 199...

Cultural region traditionally inhabited by the Sami people Sámi homeland redirects here. For the part of the Lappi administrative region in Finland, see Sámi homeland (Finland). 68°N 20°E / 68°N 20°E / 68; 20 This article needs additional citations for verification. Please help improve this article by adding citations to reliable sources. Unsourced material may be challenged and removed.Find sources: Sápmi – news · newspapers · books...

爱德华·谢瓦尔德纳泽ედუარდ შევარდნაძე第2任格鲁吉亚總統任期1995年11月26日—2003年11月23日前任茲維亞德·加姆薩胡爾季阿继任米哈伊尔·萨卡什维利苏联外交部部长任期1985年7月2日—1990年12月20日总书记米哈伊尔·戈尔巴乔夫前任安德烈·葛罗米柯继任亚历山大·别斯梅尔特内赫 个人资料出生(1928-01-25)1928年1月25日苏联外高加索苏维埃联邦社会主义共和国古...

此条目序言章节没有充分总结全文内容要点。 (2019年3月21日)请考虑扩充序言,清晰概述条目所有重點。请在条目的讨论页讨论此问题。 哈萨克斯坦總統哈薩克總統旗現任Қасым-Жомарт Кемелұлы Тоқаев卡瑟姆若马尔特·托卡耶夫自2019年3月20日在任任期7年首任努尔苏丹·纳扎尔巴耶夫设立1990年4月24日(哈薩克蘇維埃社會主義共和國總統) 哈萨克斯坦 哈萨克斯坦政府...

Artikel ini perlu diwikifikasi agar memenuhi standar kualitas Wikipedia. Anda dapat memberikan bantuan berupa penambahan pranala dalam, atau dengan merapikan tata letak dari artikel ini. Untuk keterangan lebih lanjut, klik [tampil] di bagian kanan. Mengganti markah HTML dengan markah wiki bila dimungkinkan. Tambahkan pranala wiki. Bila dirasa perlu, buatlah pautan ke artikel wiki lainnya dengan cara menambahkan [[ dan ]] pada kata yang bersangkutan (lihat WP:LINK untuk keterangan lebih lanjut...

هذه المقالة عن قناة الجزيرة. لمعانٍ أخرى، طالع جزيرة (توضيح). الجزيرة معلومات عامة المالك شبكة الجزيرة الإعلامية المؤسس حمد بن خليفة آل ثاني تاريخ التأسيس 1 نوفمبر 1996 تاريخ أول بث 1996 صيغة الصورة تلفاز عالي الدقة وتلفاز قياسي الدقة البلد قطر اللغة العربية القنوا...

نظرية الحوسبةصنف فرعي من نظرية جزء من علم المعلومات — علم الحاسوب[1] فروع علم الخوارزميات المواضيع خوارزمية — التعقيد الحسابي — worst-case complexity (en) — average-case complexity (en) تعديل - تعديل مصدري - تعديل ويكي بيانات نظرية الحوسبة أو النظرية الحسابية أو النظرية الاحتسابية (بالإنجليز�...

American college football season Program for the season opener against the Oregon State Beavers, held in Corvallis at Bell Field. 1940 Idaho Vandals footballConferencePacific Coast ConferenceRecord1–7–1 (0–4 PCC)Head coachTed Bank (6th season)Home stadiumNeale StadiumSeasons← 19391941 → 1940 Pacific Coast Conference football standings vte Conf Overall Team W L T W L T No. 2 Stanford $ 7 – 0 – 0 10 – 0 – ...

Seaman Recruit Michael Schultz interacts with a resident at the Singapore Cheshire Home Day Care Centre as part of a community service project in Singapore An adult daycare center is typically a non-residential facility that supports the health, nutritional, social, and daily living needs of adults in a professionally staffed, group setting. These facilities provide adults with transitional care and short-term rehabilitation following hospital discharge.[1][2] The majority of ...

British politician Crispin BluntOfficial portrait, 2020Chair of the Foreign Affairs Select CommitteeIn office18 June 2015 – 12 July 2017Preceded byRichard OttawaySucceeded byTom TugendhatParliamentary Under-Secretary of State for Prisons and Youth JusticeIn office6 May 2010 – 4 September 2012Prime MinisterDavid CameronPreceded byMaria EagleSucceeded byJeremy WrightMember of Parliament for ReigateIn office1 May 1997 – 30 May 2024Preceded bySir George GardinerSu...