Умовне математичне сподівання
|
Read other articles:

Plakat email Bizantium Cloisonné, Kekaisaran Bizantium, ca. 1100 Email, juga disebut email porselen, adalah sebuah yang terbuat dari kaca bubuk yang dipadukan pada sebuah wadah dengan cara pemanasan, biasanya bersuhu antara 750 dan[convert: unit tak dikenal]. Bubuk tersebut mencair, mengalir dan kemudian mengeras menjadi bahan lembut. Referensi Campbell, Marian. An Introduction to Medieval Enamels, 1983, HMSO for V&A Museum, ISBN 0-11-290385-1 Bacaan tambahan Collection Highlights: Art i...

Artikel ini perlu dikembangkan agar dapat memenuhi kriteria sebagai entri Wikipedia.Bantulah untuk mengembangkan artikel ini. Jika tidak dikembangkan, artikel ini akan dihapus. Artikel ini membutuhkan rujukan tambahan agar kualitasnya dapat dipastikan. Mohon bantu kami mengembangkan artikel ini dengan cara menambahkan rujukan ke sumber tepercaya. Pernyataan tak bersumber bisa saja dipertentangkan dan dihapus.Cari sumber: Cevdet Sunay – berita · surat kabar · buku&...

PaléoneurologieMoulage endocrânien naturel d'un Tyrannosaurus, avec un bulbe olfactif étendu (à gauche).modifier - modifier le code - modifier Wikidata La paléoneurologie, paléoneurobiologie ou neuropaléontologie, est l'étude de l'évolution du cerveau fondée sur l'analyse des moulages endocrâniens des vertébrés fossiles. Elle est considérée comme une sous-discipline de la paléontologie[1] et des neurosciences. Comme les autres branches de la paléontologie, elle donne un aper�...

French opera singer Jean-François Delmas circa 1908 Jean-François Delmas (14 April 1861 – 29 September 1933), or Francisque Delmas was a French bass-baritone who created roles in many French operas including Athanaël in Thaïs. Delmas was born in Lyon and studied at the Paris Conservatoire winning first prizes for operatic singing.[1] He made his debut in 1886 as Saint-Bris in Les Huguenots at the Paris Opéra.[2] He remained with that company until 1927 and rarely sang o...

Bob PaisleyOBE Bob Paisley mentre festeggia la Coppa dei Campioni 1976-1977 allo Stadio Olimpico di Roma Nazionalità Inghilterra Calcio Ruolo Allenatore (ex difensore) Termine carriera 1954 - giocatore1983 - allenatore Carriera Giovanili Bishop Auckland Squadre di club1 1939-1954 Liverpool252 (10) Carriera da allenatore 1954-1959 LiverpoolRiserve1959-1974 LiverpoolVice1974-1983 Liverpool 1 I due numeri indicano le presenze e le reti segnate, per le sole parti...

1877 1885 Élections législatives de 1881 en Ille-et-Vilaine 8 sièges le 21 aout 1881 et 4 septembre 1881 Type d’élection Élections législatives Corps électoral et résultats Population 615 480 Députés Sortant Élu Félix Martin-Feuillée Auguste Hovius Pierre Waldeck-Rousseau Eugène Durand René Brice Augustin Riban Eugène Pinault Olivier Le Gonidec de Traissan Félix Martin-Feuillée Auguste Hovius Pierre Waldeck-Rousseau Eugène Durand René Brice Eugène Pinault Pie...

Republican 2016 presidential primary in the U.S. state of Louisiana 2016 Louisiana Republican presidential primary ← 2012 March 5, 2016 (2016-03-05) 2020 → ← KYPR → Candidate Donald Trump Ted Cruz Home state New York Texas Delegate count 25 18 Popular vote 124,854 113,968 Percentage 41.45% 37.83% Candidate Marco Rubio John Kasich Home state Florida Ohio Delegate count 0 0 Popular vote 33,813...

Questa voce sull'argomento stagioni delle società calcistiche italiane è solo un abbozzo. Contribuisci a migliorarla secondo le convenzioni di Wikipedia. Segui i suggerimenti del progetto di riferimento. Voce principale: Foot Ball Club di Roma. Foot Ball Club di RomaStagione 1926-1927Sport calcio Squadra Roman Prima Divisione9º posto nel girone D 1925-1926 Si invita a seguire il modello di voce Questa pagina raccoglie le informazioni riguardanti il Foot Ball Club di Roma nelle c...

Indian lyricist (born 1980) This article may have been created or edited in return for undisclosed payments, a violation of Wikipedia's terms of use. It may require cleanup to comply with Wikipedia's content policies, particularly neutral point of view. (June 2019) This article includes a list of general references, but it lacks sufficient corresponding inline citations. Please help to improve this article by introducing more precise citations. (May 2020) (Learn how and when to remove this te...

American politician (1822–1900) This article includes a list of references, related reading, or external links, but its sources remain unclear because it lacks inline citations. Please help improve this article by introducing more precise citations. (March 2013) (Learn how and when to remove this message) Asa HodgesAsa HodgesMember of the U.S. House of Representativesfrom Arkansas's 1st districtIn officeMarch 4, 1873 – March 3, 1875Preceded byJames M. HanksSucceeded b...

Microsporidia Sporoblast ofFibrillanosema crangonycis Klasifikasi ilmiah Domain: Eukaryota (tanpa takson): Opisthokonta Kerajaan: Fungi Divisi: MicrosporidiaBalbiani, 1882[1] Classes and orders Lihat teks. Sinonim Microsporidiida Labbé, 1899 Microsporea Delphy, 1936 [1963], Levine et al., 1980[2][3] Microsporidea Corliss & Levine, 1963[4] Microspora Sprague, 1969, 1977[5] Microsporida Tuzet at al. 1971 Microsporidia merupakan kelompok parasit pemb...

This article needs additional citations for verification. Please help improve this article by adding citations to reliable sources. Unsourced material may be challenged and removed.Find sources: Tanghe County – news · newspapers · books · scholar · JSTOR (January 2021) (Learn how and when to remove this message) County in Henan, People's Republic of ChinaTanghe County 唐河县TanghoCountyFrom top to bottom, left to right: Wenfeng Pagoda (文峰塔), N...
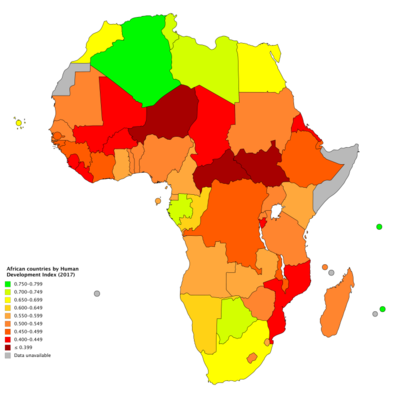
هذه المقالة يتيمة إذ تصل إليها مقالات أخرى قليلة جدًا. فضلًا، ساعد بإضافة وصلة إليها في مقالات متعلقة بها. (ديسمبر 2018) مؤشر التنمية البشرية المعروفة اختصاراً ب HDI هو مقياس مقارن لمتوسط العمر المتوقع، ومحو الأمية والتعليم ومستويات المعيشة بالنسبة للبلدان في جميع أنحاء ال�...

Transportation hub located in Bellingham, Washington Bellingham Cruise Terminal Interior of the terminal, set up for an event Vehicles waiting to drive onto a ferry docked at the terminal The Bellingham Cruise Terminal is a ferry terminal and transportation hub located in Bellingham, Washington, United States. It is near the Fairhaven neighborhood and was completed in 1989[1] and provides easy interchange between various modes of transportation. Operated by the Port of Bellingham[...

Борис Миколайович Лятошинський Борис Миколайович ЛятошинськийІм'я при народженні Борис Миколайович ЛятошинськийНародився 22 листопада (4 грудня) 1894[4][5]Житомир, Російська імперія[1]Помер 15 квітня 1968(1968-04-15)[1][2][…] (73 роки)Київ, Українська РСР, СРСР[1]...

東日本旅客鉄道が運行する快速列車については「八幡平 (列車)」をご覧ください。 八幡平 畚岳から北北東に八幡平の平坦面を見る標高 1,613.50[1] m所在地 日本岩手県八幡平市秋田県仙北市・鹿角市位置 北緯39度57分28秒 東経140度51分15秒 / 北緯39.95778度 東経140.85417度 / 39.95778; 140.85417座標: 北緯39度57分28秒 東経140度51分15秒 / 北緯39.95778度 ...

A.S.D. Basket CarugatePallacanestro Segni distintiviUniformi di gara Casa Trasferta Colori socialiBlu di Francia, Celeste, Nero, Bianco Dati societariCittàCarugate Nazione Italia ConfederazioneFIBA Europe FederazioneFIP CampionatoSerie A2 Fondazione1968 DenominazioneBasket Carugate (1968-presente) PresidenteLuciano Bellasi General managerPaolo Gavazzi AllenatoreAlberto Colombo ImpiantoPala...

2016年熊本県知事選挙 2012年 ← 2016年3月27日 (2016-03-27) → 2020年 投票率 51.01%(12.57%) 候補者 蒲島郁夫 幸山政史 寺内大介 政党 無所属 無所属 無所属 得票数 504,931 201,951 33,955 得票率 68.16% 27.26% 4.58% 選挙前知事 蒲島郁夫 無所属 選出知事 蒲島郁夫 無所属 2016年熊本県知事選挙(2016ねんくまもとけんちじせんきょ)は、2016年(平成28年)3月27日に投開票が行�...

Pour les articles homonymes, voir Oberthür. François-Charles OberthürBiographieNaissance 1er décembre 1818StrasbourgDécès 6 février 1893 (à 74 ans)6e arrondissement de ParisNationalité françaiseActivités Lépidoptériste, imprimeur, homme d'affairesPère François-Jacques Oberthür (d)Conjoint Marie Hamelin (d)Enfants Charles OberthürRené OberthürAutres informationsDistinctions Chevalier de la Légion d'honneur (1875)Chevalier de l'ordre de Saint-Grégoire-le-Grand (188...

1989 studio album by Pat Metheny GroupLetter from HomeStudio album by Pat Metheny GroupReleasedJune 29, 1989 (1989-06-29)RecordedSpring 1989StudioPower Station, New York CityGenreJazz fusion, Latin jazz, Crossover jazz, Smooth jazzLength61:39LabelGeffenProducerPat MethenyPat Metheny chronology Still Life (Talking)(1987) Letter from Home(1989) Question and Answer(1990) Professional ratingsReview scoresSourceRatingAllMusic[1] Letter from Home is the sixth studio a...








![{\displaystyle \forall A\in {\mathcal {G}},\quad \mathbb {E} \left[{\hat {X}}\mathbf {1} _{a}\right]=\mathbb {E} [X\mathbf {1} _{a}]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/5a5b80591100d66dcd80bd31132180f5c5f0db01)


![{\displaystyle \mathbb {E} [X\mid {\mathcal {G}}]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/ed9fc94f28b43063ca944aaee62a486ae9d2397f)



=\left\{{\begin{matrix}{\frac {5}{2}},&\omega =1,2\\[5pt]{\frac {25}{2}},&\omega =3,4.\end{matrix}}\right.}](https://wikimedia.org/api/rest_v1/media/math/render/svg/45d6f525aaf5073595e3273f11bdb09ae71439cd)


![{\displaystyle \mathbb {E} [X\mid {\mathcal {C}}]\equiv \mathbb {E} [X\mid \sigma ({\mathcal {C}})]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/857fd05586fd5ba1969fe326d6637c55e63d29a3)



=\left\{{\begin{matrix}{\frac {14}{3}},&\omega =1,2,3\\[5pt]16&\omega =4.\end{matrix}}\right.}](https://wikimedia.org/api/rest_v1/media/math/render/svg/6b7744f40feff93c273e092fd02638478fbf5f13)


![{\displaystyle \mathbb {E} [X\mid Y]\equiv \mathbb {E} [X\mid \sigma (Y)]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/d60061548096092acbce28b2f70c8f775b80aede)




![{\displaystyle \mathbb {E} \left[{\frac {X}{Y}}\mid Y\right]=\mathbb {E} \left[{\frac {X}{y}}\right]\mid _{y=Y}={\frac {1}{y}}\mathbb {E} [X]\mid _{y=Y}={\frac {a}{y}}\mid _{y=Y}={\frac {a}{Y}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/af0e0d7899a493a8fb20ac3d65b7f51c42695446)



![{\displaystyle \mathbb {P} (B\mid {\mathcal {G}})\equiv \mathbb {E} [\mathbf {1} _{b}\mid {\mathcal {G}}]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/ac9cd0a2284d9f5fec3f3573ecba78326db8a049)
![{\displaystyle {\hat {X}}_{1}=\mathbb {E} [X\mid {\mathcal {G}}]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/54ebd1487da17e94b8ed6d14318562e361e63dad)


![{\displaystyle {\hat {X}}_{2}=\mathbb {E} [X\mid {\mathcal {G}}]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/59cf6b49ea8c3f168cc5d485cd9bc7fd900222a3)

![{\displaystyle \mathbb {E} [X]=\mathbb {E} [\mathbb {E} [X\mid {\mathcal {G}}]]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/57a87f11a516a43087b032414d9b5454c0c9a22b)
![{\displaystyle \mathbb {P} (B)=\mathbb {E} [\mathbb {P} (B\mid {\mathcal {G}})]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/5f3b68e8f3f0afabb44efaf62f8dc8e37f89c5c2)


![{\displaystyle \mathbb {E} [X\mid {\mathcal {G}}]=\sum _{i=1}^{\infty }\mathbb {E} [X\mid C_{i}]\mathbf {1} _{C_{i}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/445d35d477f911c37b83e924cd35db163dfc6875)


![{\displaystyle {\hat {X}}=\mathbb {E} [X\mid Y]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/1374eea658b79e4b79e2a77fac442404efce5c21)



![{\displaystyle \mathbb {E} [X\mid Y=y]\equiv h(y)}](https://wikimedia.org/api/rest_v1/media/math/render/svg/e678a761ea1a8650a91dba05b00d231ca7951c44)

![{\displaystyle \mathbb {E} [X\mid {\mathcal {G}}]\geq 0}](https://wikimedia.org/api/rest_v1/media/math/render/svg/8b4ad271acd370d75dbba7074d73c8143ff1f7a5)
![{\displaystyle \mathbb {E} [X\mid {\mathcal {G}}]=\mathbb {E} [X]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/b6ce4613fc99f9f9c45c4e6987b84e3a12b89191)

![{\displaystyle \mathbb {E} [X\mid Y]=\mathbb {E} [X]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/92dc5d6a5a3e83a0f320845add16cd5fdb007446)


![{\displaystyle \mathbb {E} [\mathbb {E} [X\mid {\mathcal {G}}_{2}]\mid {\mathcal {G}}_{1}]=\mathbb {E} [X\mid {\mathcal {G}}_{1}]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/8f2c02a0cb8713f48cdcd63e9722b561957a893b)

![{\displaystyle \mathbb {E} [XY\mid {\mathcal {G}}]=X\,\mathbb {E} [Y\mid {\mathcal {G}}]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/b2cbb0898866f2d5a12486a027771a0654394f16)
![{\displaystyle \mathbb {E} [\mathbb {E} (X\mid Y)]=\mathbb {E} (X)}](https://wikimedia.org/api/rest_v1/media/math/render/svg/5effaee5360c904f3fc722d5d7878bb4ed6abd8f)



![{\displaystyle \mathbb {E} [X\mid Y]=\sum \limits _{j=1}^{\infty }\mathbb {E} [X\mid Y=y_{j}]\mathbf {1} _{\{Y=y_{j}\}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/646e4b20778f8f2e9b30599d6a66c0406dfbc4f0)
![{\displaystyle \mathbb {E} [X\mid Y=y_{j}]=\mathbb {E} _{j}[X]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/5d1ee21dd5319cf1cc42c7ff347d79baa3682a33)


![{\displaystyle \mathbb {E} [X\mid Y=y_{j}]=\sum \limits _{i=1}^{\infty }x_{i}\ \mathbb {P} (X=x_{i}\mid Y=y_{j})=\sum \limits _{i=1}^{\infty }x_{i}\ p_{X\mid Y}(x_{i}\mid y_{j})}](https://wikimedia.org/api/rest_v1/media/math/render/svg/db3f8352ac346661ddaf05e8edf1cd4d56eb0424)






![{\displaystyle \mathbb {E} [X\mid Y]=h(Y)}](https://wikimedia.org/api/rest_v1/media/math/render/svg/e71370e8081c2a93c477e1848cc4ab1398294aae)


![{\displaystyle \mathbb {E} [X\mid Y=y_{j}]=\int \limits _{-\infty }^{\infty }x\,f_{X\mid Y}(x\mid y_{j})\,dx}](https://wikimedia.org/api/rest_v1/media/math/render/svg/0802ad1de9322d6fab452c1b6fbb3fbf4a7f3835)

![{\displaystyle \langle X,Y\rangle \equiv \mathbb {E} [XY],\;\forall X,y\in L^{2}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/f7e5033959216d05661463710370b4438dba844f)
![{\displaystyle \|X\|={\sqrt {\mathbb {E} \left[X^{2}\right]}},\;\forall X\in L^{2}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/20d42cfe974e7b1474b921f9e24c83819782fdf1)


![{\displaystyle \Pi _{L_{\mathcal {G}}^{2}}(X)=\mathbb {E} [X\mid {\mathcal {G}}]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/1fe350c398706acd87323a4d9d8956249e232b0c)
![{\displaystyle \|X-\mathbb {E} [X\mid {\mathcal {G}}]\|=\inf \limits _{Z\in L_{\mathcal {G}}^{2}}\|X-Z\|}](https://wikimedia.org/api/rest_v1/media/math/render/svg/1575510844d711229f176603d493445a23571feb)
![{\displaystyle \langle X,Z\rangle =\langle \mathbb {E} [X\mid {\mathcal {G}}],Z\rangle ,\;\forall Z\in L_{\mathcal {G}}^{2}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/74ec6c4576d9733990d055a63278d87215eb4693)
