Темна рідина

Серія статей:
Фізична космологія
Full-sky image derived from nine years' WMAP data
Ранній всесвіт
Передумови
Розширення · Майбутнє
Компоненти · Структура
Компоненти
Структура
Експерименти[en]
Науковці
Фізична космологія

В астрономії і космології поняття темна рідина є альтернативою теорії як темної матерії, так і темної енергії й намагається пояснити обидва явища в єдиній структурі[1][2].

Гіпотеза про темну рідину передбачає, що темна матерія і темна енергія не є окремими фізичними явищами, як вважалося раніше, і не мають окремого походження, але вони тісно пов'язані одна з одною і можуть розглядатися як дві грані однієї рідини. В галактичних масштабах темна рідина поводиться як темна матерія, а в більших масштабах її поведінка стає схожим на темну енергію. Наші спостереження в масштабах Землі і Сонячної системи в даний час є недостатніми для пояснення гравітаційних ефектів, які спостерігаються в таких великих масштабах. Було показано, що простій темній рідині з негативною масою притаманні властивості, необхідні для пояснення як темної матерії, так і темної енергії[3][4].

Огляд

Останнім часом в астрофізиці і космології виникли дві головні загадки, пов'язані з законами гравітації. Першим було усвідомлення того, що всередині галактик недостатньо видимих зірок або газу, щоб пояснити їх високу швидкість обертання. Теорія темної матерії була створена, щоб пояснити це явище. Вона передбачає, що галактики обертаються так швидко, тому що в галактиках (включаючи наш власний Чумацький Шлях) більше речовини, ніж можна побачити, якщо тільки підрахувати масу зірок і газу, і що ця (темна) матерія невидима, тому що вона не взаємодіє з електромагнітними силами, з якої виходять всі форми світла.

Друга загадка виникла зі спостережень дуже специфічного виду наднових, відомих як наднові типу Ia, що використовуються як «стандартні свічки»: коли вони порівнювалися у віддалених і прилеглих галактиках, було виявлено, що віддалена наднова слабкіше, і, як виявилося, далі, ніж очікувалося. Це означало, що Всесвіт не тільки розширювався, але і прискорював своє розширення. Теорія темної енергії була створена, щоб пояснити це явище.

Традиційний підхід до моделювання ефектів гравітації передбачає, що загальна відносність так само вірна в космологічних масштабах, як і в Сонячній системі, де її передбачення були перевірені більш точно. Однак не зміна правил гравітації має на увазі присутність темної матерії та темної енергії в частинах Всесвіту, де кривина просторово-часового різноманіття набагато менше, ніж в Сонячній системі. Феноменологічно можливо змінити рівняння гравітації в областях малої кривини простору-часу так, що динаміка простору-часу викликає те, що ми приписуємо присутності темної матерії та темної енергії[5]. Теорія темної рідини передбачає, що темна рідина являє собою особливий вид рідини, притягувальна і відштовхувальна поведінка якої залежить від локальної щільності енергії. У цій теорії темна рідина поводиться як темна матерія в областях простору, де щільність баріонів висока. Ідея полягає в тому, що, коли темна рідина знаходиться в присутності речовини, вона сповільнюється і коагулює навколо неї; тоді це привертає більше темної рідини, щоб згортатися навколо неї, таким чином посилюючи силу гравітації біля неї. Ефект завжди присутній, але стає помітним тільки в присутності дуже великої маси, такої як галактика. Це опис аналогічно теоріям темної матерії, і окремий випадок рівнянь темної рідини відтворює темну матерію.

З іншого боку, в місцях, де відносно мало матерії, як, наприклад, в пустотах між надскупченнями галактик, ця теорія передбачає, що темна рідина послаблюється і набуває негативний тиск. Таким чином, темна рідина стає силою відштовхування, з ефектом, подібним з ефектом темної енергії.

Темна рідина виходить за межі темної матерії та темної енергії в тому сенсі, що вона пророкує безперервний діапазон притягувальних і відштовхувальних якостей при різних випадках щільності речовини. Дійсно, окремі випадки різних інших теорій гравітації відтворюються темною рідиною, наприклад, інфляція, квінтесенція, k-сутність, f(R), узагальнений айнштайнівський ефір f(K)[en], MOND, TeVeS, BSTV і т. д. Теорія темної рідини також пропонує нові моделі, такі як певна модель f (K + R), яка пропонує цікаві[уточнити] поправки до MOND, які залежать від червоного зсуву і щільності.

Спрощувальні припущення

Теорія темної рідини не розглядається як стандартна модель механіки рідини, тому що багато рівнянь механіки рідини занадто важко вирішити повністю. Формалізований гідродинамічний підхід, такий як узагальнена модель газу Чаплигіна, був би ідеальним методом для моделювання цієї теорії, але в даний час він вимагає занадто великої кількості точок даних спостережень, щоб бути здійсненним в обчислювальному відношенні, також ще недостатньо таких точок даних для космологів. Замість цього було розпочато крок спрощення, шляхом моделювання теорії за допомогою моделей скалярного поля, як це робиться в інших альтернативних підходах до темної енергії і темної матерії[2][6].

Див. також

Джерела

  1. ↑ Arbey, Alexandre (2005). Is it possible to consider Dark Energy and Dark Matter as a same and unique Dark Fluid?. doi:10.48550/ARXIV.ASTRO-PH/0506732. Процитовано 20 вересня 2024.
  2. ↑ а б Arbey, Alexandre (2006). Dark Fluid: a complex scalar field to unify dark energy and dark matter. doi:10.48550/ARXIV.ASTRO-PH/0601274. Процитовано 20 вересня 2024.
  3. ↑ Farnes, J. S. (2018-12). A unifying theory of dark energy and dark matter: Negative masses and matter creation within a modified ΛCDM framework. Astronomy & Astrophysics. 620: A92. doi:10.1051/0004-6361/201832898. ISSN 0004-6361. Процитовано 20 вересня 2024.
  4. ↑ Farnes, Jamie (5 грудня 2018). Bizarre ‘dark fluid’ with negative mass could dominate the universe – what my research suggests. The Conversation (амер.). Процитовано 20 вересня 2024.
  5. ↑ Exirifard, Qasem (2008). Phenomenological covariant approach to gravity. arXiv (англ.). doi:10.48550/ARXIV.0808.1962. Процитовано 20 вересня 2024.
  6. ↑ Arbey, Alexandre; Mahmoudi, Farvah (2007). One-loop quantum corrections to cosmological scalar field potentials. doi:10.48550/ARXIV.HEP-TH/0703053. Процитовано 20 вересня 2024.

Посилання

Read other articles:

Western European Summer Time

Fusi orari dell'Europa: Azzurro Western European Time (UTC+0) Blu Western European Time (UTC+0)Western European Summer Time (UTC+1) Rosso Central European Time (UTC+1)Central European Summer Time (UTC+2) Giallo Ora di Kaliningrad (UTC+2). Ocra Eastern European Time (UTC+2)Eastern European Summer Time (UTC+3) Verde Ora di Mosca (UTC+3) I colori più chiari indicano i paesi che non osservano l'ora legale Il Western European Summer Time, abbreviato come WEST, è il fuso orario artificiale adotta...

 

Natrium hipoklorit

Natrium hipoklorit Kation natriumKation natrium Model ruang terisi anion hipokloritAnion hipoklorit Nama Nama IUPAC Natrium hipoklorit Nama lain AntiforminPemutihKlorida dari sodaDalam larutan encer:Larutan Carrel-DakinLarutan Dakin modifikasiLarutan soda klorinasi untuk bedah Penanda Nomor CAS 7681-52-9 (anhidrat)[1]7681-52-8 (pentahidrat)[1] Model 3D (JSmol) Gambar interaktif 3DMet {{{3DMet}}} ChEBI CHEBI:32146 Y ChemSpider 22756 Y Nomor EC KEGG D01711&#...

 

Jean-Pierre Fourcade

Pour les articles homonymes, voir Fourcade. Jean-Pierre Fourcade Jean-Pierre Fourcade en 2009. Fonctions Maire de Boulogne-Billancourt 25 juin 1995 – 17 mars 2007(11 ans, 8 mois et 20 jours) Élection 18 juin 1995 Réélection 18 mars 2001 Prédécesseur Paul Graziani Successeur Pierre-Mathieu Duhamel Président de la commission desAffaires sociales du Sénat 25 septembre 1983 – 27 septembre 1998(15 ans et 2 jours) Élection 25 septembre 1983 Prédécesseur Rober...

The Magic Goes Away

1978 novella by Larry Niven The Magic Goes AwayShort story by Larry NivenCover for the illustrated edition, art by Boris Vallejo.CountryUnited StatesLanguageEnglishGenre(s)FantasyPublicationPublication date1976 The Magic Goes Away is a fantasy short story written by Larry Niven in 1976, and later expanded to a novella of the same name which was published in 1978. While these works were not the first in the Magic Universe or Warlock series, they marked a turning point after the 1973 oil crisis...

 

1982 AIAW National Division I Basketball Championship

1982 AIAW National Division I Basketball ChampionshipTournament informationDatesMarch 21, 1982–March 28, 1982AdministratorAssociation for Intercollegiate Athletics for WomenVenue(s)Philadelphia, PennsylvaniaParticipants16Final positionsChampionsRutgersRunner-upTexasTournament statisticsMatches played15← 19811983 (NCAA Division I)1983 (NCAA Division II)1983 (NCAA Division III)1983 (NAIA) → The 1982 AIAW National Division I Basketball Championship was held on March...

 

وارين هاستينغز

هذه المقالة تحتاج للمزيد من الوصلات للمقالات الأخرى للمساعدة في ترابط مقالات الموسوعة. فضلًا ساعد في تحسين هذه المقالة بإضافة وصلات إلى المقالات المتعلقة بها الموجودة في النص الحالي. (مارس 2018) وارين هاستينغز (بالإنجليزية: Warren Hastings)‏    معلومات شخصية الميلاد 6 ديسمبر 1732...

Public Prosecution Service of Canada

Government agency Public Prosecution Service of CanadaService des poursuites pénales du CanadaAgency overviewFormed2006 (2006)PrecedingFederal Prosecution ServiceJurisdictionCanadaHeadquarters160 Elgin Street – 12th Floor, Ottawa, Ontario, K1A 0H8Employees1040170 private-sector law firms432 individually appointed lawyersAnnual budget$201,300,000 (2018–19)[1]Minister responsibleHon. Arif Virani, Attorney General of CanadaAgency executiveKathleen Roussel, Director of Public Pr...

 

大字 (数字)

この項目には、一部のコンピュータや閲覧ソフトで表示できない文字が含まれています（詳細）。 数字の大字（だいじ）は、漢数字の一種。通常用いる単純な字形の漢数字（小字）の代わりに同じ音の別の漢字を用いるものである。 概要 壱万円日本銀行券（「壱」が大字） 弐千円日本銀行券（「弐」が大字） 漢数字には「一」「二」「三」と続く小字と、「壱」「�...

 

Gereja negara Kekaisaran Romawi

Kaisar Theodosius I, yang menjadikan Kekristenan Nicea sebagai gereja negara Kekaisaran Romawi. Kekristenan Nicea menjadi gereja negara Kekaisaran Romawi dengan dikeluarkannya Maklumat Tesalonika pada tahun 380 M, ketika Kaisar Theodosius I menjadikannya agama resmi Kekaisaran Romawi.[1][2] Gereja Ortodoks Timur, Gereja Ortodoks Oriental, dan Gereja Katolik, masing-masing mengklaim sebagai kelanjutan historis dari gereja ini dalam bentuk aslinya, tetapi tidak mengidentifikasik...

Gürcü Mehmed Pascià II

Disambiguazione – Gürcü Mehmed Pascià II rimanda qui. Se stai cercando il Gran Visir che governò dal 21 settembre 1622 al 5 febbraio 1623, vedi Gürcü Mehmed Pascià. Gürcü Mehmed Pascià Gran visir dell'Impero ottomanoDurata mandato27 settembre 1651 –20 giugno 1652 MonarcaMehmed IV PredecessoreAbaza Siyavush Pascià I (I mandato) SuccessoreTarhuncu Ahmed Pascià Gürcü Mehmed Pascià (il Georgiano; ... – Buda, 1665) è stato un politico ottomano. Fu schia...

 

Jodie Taylor

For the English fantasy author, see Jodi Taylor. English footballer Jodie Taylor Taylor with England.Personal informationFull name Jodie Lee Taylor[1]Date of birth (1986-05-17) 17 May 1986 (age 37)[1]Place of birth Birkenhead, Merseyside, EnglandHeight 5 ft 6 in (1.68 m)[1]Position(s) Striker[1]Youth career Tranmere RoversCollege careerYears Team Apps (Gls)2004–2007 Oregon State Beavers (47)Senior career*Years Team Apps (Gls)2002–2004 Tr...

 

Armand Cure

Questa voce sugli argomenti giocatori di football americano statunitensi e cestisti statunitensi è solo un abbozzo. Contribuisci a migliorarla secondo le convenzioni di Wikipedia. Segui i suggerimenti del progetto di riferimento. Armand Cure Nazionalità  Stati Uniti Altezza 183 cm Peso 90 kg Pallacanestro Ruolo Ala Termine carriera 1947 CarrieraGiovanili New Bedford High School1940-1943 R. Island RamsSquadre di club 1946-1947 Prov. Steamrollers12 Il simbolo → indica u...

Grateful Dead discography

Cataloging of published recordings by the Grateful Dead Grateful Dead discographyThe Steal Your Face image is one of the Grateful Dead's official logos.Studio albums13Live albums10Compilation albums10Video albums10Singles27Box sets8Retrospective live albums83Dick's Picks36Digital Download series15Road Trips17Dave's Picks50 The discography of the rock band the Grateful Dead includes more than 200 albums, the majority of them recorded live in concert. The band has also released more than two do...

 

世界政區索引

此條目可能包含不适用或被曲解的引用资料，部分内容的准确性无法被证實。 (2023年1月5日)请协助校核其中的错误以改善这篇条目。详情请参见条目的讨论页。 各国相关 主題列表 索引 国内生产总值 石油储量 国防预算 武装部队（军事） 官方语言 人口統計 人口密度 生育率 出生率 死亡率 自杀率 谋杀率 失业率 储蓄率 识字率 出口额 进口额 煤产量 发电量 监禁率 死刑 国债 ...

 

Ad Caeli Reginam

Botticelli, pemahkotaan Sang Perawan Suci Maria di surga Ad caeli reginam adalah sebuah ensiklik dari Paus Pius XII, diberikan di Roma, dari Basilika Santo Petrus, pada hari perayaan Kebundaan Perawan Suci Maria, pada hari kesebelas bulan Oktober 1954, pada tahun ke-16 masa kepausannya. Ensiklik ini merupakan suatu unsur penting dari Mariologi Paus Pius XII. Dokumen ini membentuk hari perayaan Keratuan Maria. Sumber Paus Pius XII, ensiklik dan bulla Mariologi: Encyclical Fulgens Corona on the...

French Argentines

Argentines of French birth or descent Ethnic group French ArgentinesFranco-ArgentinFranco-argentino Total population6 000 000 ' 17% of Argentina's population[1][better source needed]Regions with significant populationsThroughout Argentina, specially in Central Argentina.LanguagesRioplatense Spanish. Minorities speak French, Occitan and Basque.ReligionPredominantly Roman CatholicismRelated ethnic groupsArgentines of European descent · French people ...

 

Preston Brooks

American politician (1819–1857) Not to be confused with Preston Brook. Preston BrooksMember of the U.S. House of Representativesfrom South Carolina's 4th districtIn officeAugust 1, 1856 – January 27, 1857Preceded byHimselfSucceeded byMilledge BonhamIn officeMarch 4, 1853 – July 15, 1856Preceded byJohn McQueenSucceeded byHimselfMember of the South Carolina House of Representativesfrom the Edgefield County districtIn officeNovember 25, 1844 �...

 

François-Henri Pinault

François-Henri PinaultFrançois-Henri PinaultLahir28 Mei 1962 (umur 62)Rennes, Republik Keempat PrancisTempat tinggalParis, PrancisKebangsaanPrancisAlmamaterHEC ParisPekerjaanPebisnisGelarChairman dan CEO, KeringSuami/istriSalma Hayek François-Henri Pinault (bahasa Prancis: [pino]; lahir 28 Mei 1962 [butuh rujukan]) adalah seorang pengusaha Prancis, dan presiden konglomerat merek mewah, serta putra dan pewaris François Pinault. Dia dianggap sebagai salah satu orang terka...

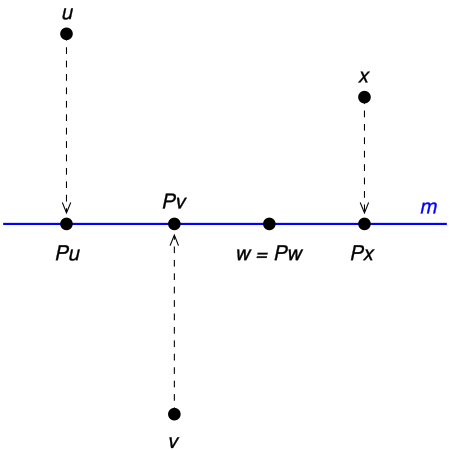
Proiezione (geometria)

Disambiguazione – Se stai cercando il metodo di rappresentazione grafica, vedi Proiezioni ortogonali. La proiezione ortogonale di un cubo su un piano verticale. In algebra lineare e analisi funzionale, una proiezione è una trasformazione lineare P {\displaystyle P} definita da uno spazio vettoriale in sé stesso (endomorfismo) che è idempotente, cioè tale per cui P 2 = P {\displaystyle P^{2}=P} : applicare due volte la trasformazione fornisce lo stesso risultato che applicandola una vol...

 

Calcasieu Parish, Louisiana

Parish in Louisiana, United States This article needs additional citations for verification. Please help improve this article by adding citations to reliable sources. Unsourced material may be challenged and removed.Find sources: Calcasieu Parish, Louisiana – news · newspapers · books · scholar · JSTOR (November 2021) (Learn how and when to remove this message) Parish in Louisiana, United StatesCalcasieu Parish, LouisianaParishParish of CalcasieuCalcas...