Регулярна міра
|
Read other articles:

Jesenwang Lambang kebesaranLetak Jesenwang di Fürstenfeldbruck NegaraJermanNegara bagianBayernWilayahOberbayernKreisFürstenfeldbruckMunicipal assoc.Mammendorf Pemerintahan • MayorJohann Wieser (Wählergruppe Einigkeit)Luas • Total15,30 km2 (590 sq mi)Ketinggian558 m (1,831 ft)Populasi (2013-12-31)[1] • Total1.490 • Kepadatan0,97/km2 (2,5/sq mi)Zona waktuWET/WMPET (UTC+1/+2)Kode pos82287Kode area telep...

Bell Eagle Eye, Model 918, adalah kendaraan udara tak berawak tiltrotor Amerika Serikat yang ditawarkan sebagai salah satu pesaing di program VT-UAV (Vertical Takeoff - Unmanned Aerial Vehicle) Angkatan Laut AS. Program Eagle Eye dimulai pada tahun 1993 dengan skala prototipe 7/8 TR911X. Referensi This article contains material that originally came from the web article Unmanned Aerial Vehicles by Greg Goebel, which exists in the Public Domain. Pranala luar Wikimedia Commons memiliki media men...

DarsojoPengabdianIndonesiaDinas/cabang TNI Angkatan DaratPangkat Mayor Jenderal TNINRP21803KesatuanZeni (CZI)Mayor Jenderal TNI (Purn.) Darsojo merupakan seorang perwira tinggi angkatan darat dari Indonesia.[1] Pendidikan Koninklijke Militaire Academie (KMA) Breda[1] Kursus Reguler Sekolah Staf dan Komando Angkatan Darat (1968)[1] Karier militer Komandan Batalyon Zeni Tempur 7 Komando Cadangan Strategis Angkatan Darat (1968?)[1] Wakil Asisten Perencanaan dan An...

Bộ trưởng Bộ Xây dựngViệt NamQuốc huy Việt NamQuốc kỳ Việt NamĐương nhiệmNguyễn Thanh Nghịtừ 08 tháng 04 năm 2021Bộ Xây dựngChức vụBộ trưởng(thông dụng)Đồng chí Bộ trưởngThành viên củaBan Chấp hành Trung ương ĐảngChính phủ Việt NamBáo cáo tớiThủ tướngTrụ sở37 Lê Đại Hành, Hà NộiBổ nhiệm bởiChủ tịch nướctheo sự đề cử của Thủ tướng Chính phủNhiệm kỳKhông nhi...

معتمدية الشابة الإحداثيات 35°14′20″N 11°03′20″E / 35.23895°N 11.05567°E / 35.23895; 11.05567 تقسيم إداري البلد تونس[1] التقسيم الأعلى ولاية المهدية معلومات أخرى منطقة زمنية ت ع م+01:00 رمز جيونيمز 7870311 تعديل مصدري - تعديل معتمدية الشابة إحدى معتمديات الجمهور...

العلاقات السنغافورية اللوكسمبورغية سنغافورة لوكسمبورغ سنغافورة لوكسمبورغ تعديل مصدري - تعديل العلاقات السنغافورية اللوكسمبورغية هي العلاقات الثنائية التي تجمع بين سنغافورة ولوكسمبورغ.[1][2][3][4][5] مقارنة بين البلدين هذه مقارنة عامة و...

The Planetary Society's contribution to the failed Fobos-Grunt mission (2011) Living Interplanetary Flight Experiment'LIFE' Bio-ModuleMission typeAstrobiological experiment on board the Fobos-Grunt spacecraft.OperatorThe Planetary SocietyWebsitewww.planetary.orgMission duration3 years (planned) Spacecraft propertiesManufacturerNPO LavochkinLaunch mass<100 g (3.5 oz) Start of missionLaunch dateNovember 8, 2011,[1]RocketZenit-2SBLaunch siteBaikonur 45/1ContractorRoscosmosDe...

2001 2008 Élections cantonales de 2004 dans l'Aisne 21 des 42 cantons de l'Aisne 21 et 28 mars 2004 Type d’élection Élections cantonales Corps électoral et résultats Inscrits 177 528 Votants au 1er tour 115 782 Votes exprimés au 1er tour 111 330 Votants au 2d tour 80 919 Votes exprimés au 2d tour 76 824 PS – Yves Daudigny Majorité départementale PSDVGPCF Voix au 1er tour 31 897 47,45 % Voix au 2e tour 38 847 50,56 %...

Altar khusus untuk Niu Tou Ma Mian dalam Festival Perjamuan Arwah di Kong Fuk Miau, Pulau Bangka. Niu Tou dan Ma Mian dilukiskan pada Gulungan Akhirat di Museum Nasional Nara Gû-thâu dan Bé-bīn adalah sepasang penjaga menakutkan dari Di Yu (akhirat) dalam Mitologi Tiongkok, tempat roh yang sudah meninggal akan menerima pengadilan atas perbuatan mereka sebelum bereinkarnasi. Sebagaimana arti nama mereka, Gû-thâu memiliki kepala kerbau dan Bé-bīn berkepala kuda. Mereka disebut Ngau Tau ...

Brunei Darussalam Artikel ini adalah bagian dari seri Politik dan KetatanegaraanBrunei Darussalam Sultan Hassanal Bolkiah Konstitusi Dewan Penasihat Perdana Menteri Hassanal Bolkiah Kabinet Dewan Suksesi Dewan Agama Islam Dewan Legislatif Yudikatif Pengadilan Sipil Pengadilan Syariah Pembagian administratif DistrikMukimDesaKota Hubungan luar negeri Menteri Luar Negeri Melayu Islam Beraja (Kerajaan Melayu Islam)(filsafat nasional) Negara lainnya Atlas lbs Wazir merupakan salah satu golongan pe...

Pertempuran KöniggrätzBagian dari Perang Austria-PrusiaPertempuran Königgrätz, 3 Juli 1866 buatan Christian Sell. Litografi, 1866.Tanggal3 Juli 1866LokasiSadová, Bohemia, Republik Ceko pada masa sekarang50°13′N 15°50′E / 50.21°N 15.83°E / 50.21; 15.83Koordinat: 50°13′N 15°50′E / 50.21°N 15.83°E / 50.21; 15.83Hasil Kemenangan PrusiaPihak terlibat Prusia Austria SaxonyTokoh dan pemimpin Helmuth von Moltke Pangeran Friedrich Ka...

Katedral MiamiKatedral Santa Mariabahasa Inggris: The Cathedral of Saint Marybahasa Spanyol: Catedral de Santa Maríabahasa Kreol Haiti: Katedral Sen MariKatedral Miami25°50′38″N 80°12′01″W / 25.843963°N 80.200219°W / 25.843963; -80.200219Koordinat: 25°50′38″N 80°12′01″W / 25.843963°N 80.200219°W / 25.843963; -80.200219Lokasi7525 NW 2nd Ave.Miami, FloridaNegaraAmerika SerikatDenominasiGereja Katolik RomaSitus ...

烏克蘭總理Прем'єр-міністр України烏克蘭國徽現任杰尼斯·什米加尔自2020年3月4日任命者烏克蘭總統任期總統任命首任維托爾德·福金设立1991年11月后继职位無网站www.kmu.gov.ua/control/en/(英文) 乌克兰 乌克兰政府与政治系列条目 宪法 政府 总统 弗拉基米尔·泽连斯基 總統辦公室 国家安全与国防事务委员会 总统代表(英语:Representatives of the President of Ukraine) 总...

محافظة بنه دنه الاسم الرسمي (بالفيتنامية: Bình Định) الإحداثيات 14°10′00″N 109°00′00″E / 14.166666666667°N 109°E / 14.166666666667; 109 [1] تقسيم إداري البلد فيتنام[2][3] التقسيم الأعلى فيتنام العاصمة كوي نهون [لغات أخرى] التقسيمات الإدار�...

Ottoman, Safavid and Mughal empires from the 16th to 18th centuries This article is about the Ottoman, Safavid and Mughal empires. For the novel, see Gunpowder Empire. Map of Gunpowder empires Mughal Army artillerymen during the reign of Akbar. A mufti sprinkling cannon with rose water The gunpowder empires, or Islamic gunpowder empires, is a collective term coined by Marshall G. S. Hodgson and William H. McNeill at the University of Chicago, referring to three early modern Muslim empires: th...

British phonetician (1881–1967) This article includes a list of general references, but it lacks sufficient corresponding inline citations. Please help to improve this article by introducing more precise citations. (June 2021) (Learn how and when to remove this message) Daniel JonesDaniel Jones, age 40Born(1881-09-12)12 September 1881London, EnglandDied4 December 1967(1967-12-04) (aged 86)Gerrards Cross, Buckinghamshire, EnglandNationalityBritishEducationUniversity of CambridgeOccupati...

Francis W. Pickens 69º Governatore della Carolina del SudDurata mandato14 dicembre 1860 –17 dicembre 1862 PredecessoreWilliam H. Gist SuccessoreMilledge L. Bonham Ambasciatore degli Stati Uniti d'America nell'Impero russoDurata mandato11 giugno 1858 –9 settembre 1860 PresidenteJames Buchanan PredecessoreThomas H. Seymour SuccessoreJohn Appleton Membro della Camera dei rappresentanti - Carolina del SudDurata mandato8 dicembre 1834 –3 marzo 1843 ...

English Tudor poet and antiquary John LelandLine engraving by Charles Grignion the Elder (1772), purportedly taken from a bust of John Leland at All Souls College, Oxford.[1] Sculptor Louis François Roubiliac (d. 1762) probably created the original bust.[2]Born13 September c. 1503LondonDied18 April 1552Resting placeparish church of St Michael-le-Querne, London[2]51°30′46″N 0°05′51″W / 51.512778°N 0.0975°W / 51.512778; -0.0975M...
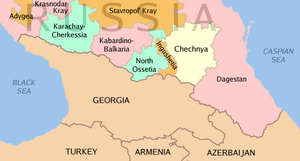
Militant attack during the Second Chechen War in Russia 2005 raid on NalchikPart of the Second Chechen WarAftermath of the raid, a garage in which terrorists held outDate8:20 AM, October 13, - 2:00 PM, October 14, 2005 (27:40 hours)LocationNalchik, Kabardino-Balkaria, RussiaResult Russian victoryBelligerents Russia Kabardino-Balkaria Yarmuk Jamaat Caucasian Front (militant group)Commanders and leaders Saidli Shibzukhov Overall:Commander Shamil BasayevMusa Artur MukozhevOperational...

Untuk kegunaan lain, lihat Siantar (disambiguasi). Siantar BaratKecamatanKantor Kecamatan Siantar BaratPeta lokasi Kecamatan Siantar BaratNegara IndonesiaProvinsiSumatera UtaraKotaPematangsiantarPemerintahan • CamatPardomuan Nasution, SS, MSPPopulasi • Total45,291 jiwa jiwaKode Kemendagri12.72.02 Kode BPS1273030 Luas3,21 km²Desa/kelurahan8 Siantar Barat adalah sebuah kecamatan di Kota Pematangsiantar, Sumatera Utara, Indonesia. Pembentukan Kecamatan Siantar Barat...

























![{\displaystyle A_{n}=[-n,\ n]\cap A.}](https://wikimedia.org/api/rest_v1/media/math/render/svg/61ebfe97eec799e3ee56772a5913a0f3d4d665b2)














