Проліферація

Клітинний цикл і зростання
Схема поділу, росту та проліферації клітин.

Проліфера́ція[1] (лат. proliferatio, від proles — «потомство» і ferre — «нести») — процес розростання тканини тварини через поділ та ріст клітин організму. Проліферація клітин відбувається шляхом поєднання росту клітин із регулярними клітинними циклами «G1-S-M-G2» для виробництва багатьох диплоїдних клітин. Вона вимагає, щоб ріст і поділ клітин відбувалися одночасно, таким чином, середній розмір клітин залишається незмінним у популяції. Поділ клітин може відбуватися без росту клітини, поступово утворюючи багато менших клітин (як при розщепленні зиготи), в той час, як ріст клітини може відбуватися без поділу клітини з утворенням однієї більшої клітини (як при зростанні нейронів).

Збільшення клітин в організмі збалансовано їхньою загибеллю, диференціацією та переходом у стадію G0 клітинного циклу — такі клітини не здатні до поділу, тому не призводять до розростання тканин[2]. Загальна кількість клітин у популяції визначається швидкістю проліферації клітин мінус швидкість загибелі клітини.

В одноклітинних організмах проліферація клітин значною мірою реагує на доступність поживних речовин у навколишньому середовищі (або в лабораторному).

У багатоклітинних організмах процес проліферації клітин контролюється генними регуляторними мережами, закодованими в геномі і виконується в основному за допомогою факторів транскрипції, зокрема тими, що регулюються шляхами передачі сигналу, викликаними факторами росту під час міжклітинної комунікації в процесі розвитку[3].

Клітинна проліферація збільшується під час малігнізації тканин і переході їх на пухлини. Неконтрольована проліферація клітин, що призводить до збільшення її швидкості, або нездатність клітин зупинити своє розмноження в нормальний час, є причиною раку.

В рослин теж саме, що проліфікація.

Див. також

Примітки

  1. ↑ Проліферація : Алфавітний покажчик. Словник іншомовних слів (англ.). Процитовано 17 грудня 2021.
  2. ↑ Cell proliferation, definition. Nature.
  3. ↑ Томпсон, Баррі Джеймс (2010). Developmental control of cell growth and division in Drosophila. Current Opinion in Cell Biology. 22 (6): 788—794. doi:10.1016/j.ceb.2010.08.018. PMID 20833011.

Посилання

Вікісховище має мультимедійні дані за темою: Проліферація


Тигр Це незавершена стаття із зоології.
Ви можете допомогти проєкту, виправивши або дописавши її.

Read other articles:

Ekkathat

EkkathatเอกทัศRaja AyutthayaPenggambaran Raja Ekkathat atau Raja Uthumphon versi lukisan Burma (kemungkinan), British Library, LondonRaja AyutthayaBerkuasa1758–1759/17601762-7 April 1767PendahuluUthumphonPenerusTaksin (setelah Ayutthaya jatuh, sebagai Raja Kerajaan Thonburi)Informasi pribadiKelahiran1718Kerajaan AyutthayaKematian17 April 1767Hutan Ban Chik, AyutthayaWangsaDinasti Ban Phlu LuangAyahBorommakotIbuPhiphitmontriPasanganMaengmao, Putri Wimonphat Borommaracha Kasat Bow...

 

 

Brigata aerea

La brigata aerea è una grande unità militare, articolazione operativa tipica di alcune aeronautiche militari. Dal punto di vista dell'organica, la brigata aerea viene equiparata alla brigata per le forze di terra. Grado per paramano di generale di brigata aerea. Il concetto di brigata prevede l'interazione e il controllo di due o più stormi, che ne dipendono gerarchicamente, e risponde al comando di un generale di brigata aerea pilota, o da un ufficiale di grado equivalente. Indice 1 Itali...

 

 

Suaka Margasatwa Selous

Suaka Margasatwa SelousIUCN Kategori IV (Kawasan Pengelolaan Habitat/Spesies)Para gajah di Suaka Margasatwa SelousLetakTanzaniaLuas54,600 km2 (21,081 sq mi)Didirikan1922 Situs Warisan Dunia UNESCO Suaka Margasatwa Selous adalah salah satu suaka margasatwa terbesar di dunia yang terletak di selatan Tanzania. Tempat tersebut mengambil nama dari tokoh Inggris, Sir Frederick Selous, seorang pemburu suaka margasatwa terkenal dan konservasionis awal, yang tewas di Beho Beho di kawasa...

Alfons Taryadi

Artikel ini sebatang kara, artinya tidak ada artikel lain yang memiliki pranala balik ke halaman ini.Bantulah menambah pranala ke artikel ini dari artikel yang berhubungan atau coba peralatan pencari pranala.Tag ini diberikan pada Agustus 2017. Alfons TaryadiLahir(1936-05-11)11 Mei 1936 Klaten, Jawa Tengah,IndonesiaMeninggal18 Mei 2013(2013-05-18) (umur 77) Jakarta, IndonesiaPekerjaansastrawaneditorKebangsaan Indonesia Alfons Taryadi (11 Mei 1936 – 18 Mei 2013) adalah sas...

 

 

Annapolis Basin

Shallow inlet on the east coast of Nova Scotia, Canada View of Annapolis Basin from Fort Anne, at Annapolis Royal 5km3miles A n n a p o l i sV a l l e y N o r t h M o u n t a i n R a n g e D i g b yN e c k Annapolis Basin Bay of Fundy Digby Gut Bear River    Annapolis Basin is a substantial basin south of the North Mountain Range of Nova Scotia. The inlet of Digby Gut breaks through the higher ground and connects it to the Bay of Fundy. The Annapolis Basin is a sub-basin of the Bay of Fun...

 

 

Issam Hamel

Algerian rugby union player An editor has performed a search and found that sufficient sources exist to establish the subject's notability. Please help improve this article by adding citations to reliable sources. Unsourced material may be challenged and removed.Find sources: Issam Hamel – news · newspapers · books · scholar · JSTOR (February 2024) (Learn how and when to remove this template message) Rugby playerIssam HamelDate of birth (1997-06-16) 16...

Jurriën Timber

Dutch footballer (born 2001) Jurriën Timber Timber playing for Ajax in 2023Personal informationFull name Jurriën David Norman Timber[1]Date of birth (2001-06-17) 17 June 2001 (age 22)[2]Place of birth Utrecht, NetherlandsHeight 1.79 m (5 ft 10 in)[3]Position(s) DefenderTeam informationCurrent team ArsenalNumber 12Youth career DVSU2008–2014 Feyenoord2014–2018 AjaxSenior career*Years Team Apps (Gls)2018–2021 Jong Ajax 39 (0)2019–2023 Ajax 85...

 

 

Asaïb Ahl al-Haq

Pour les articles homonymes, voir AAH. Asaïb Ahl al-Haq Idéologie Islamisme chiiteVelayat-e faqih[1]Khomeinisme[2]Antioccidentalisme[3]AntiaméricanismeAnti-LGBTAntisionisme[4] Objectifs Instauration en Irak d'un gouvernement islamique chiite fondé sur le Velayat-e faqih Statut Actif Site web ahlualhaq.com Fondation Date de formation Juillet 2006 Pays d'origine Irak Actions Zone d'opération Irak, Syrie, Liban et Iran Organisation Chefs principaux Qais al-Khazali Akram al-Kaabi Membres 10...

 

 

بشيت

بشيت مقام الشيخ شيت بشيت قضاء الرملة إحداثيات 31°49′27″N 34°44′48″E / 31.82417°N 34.74667°E / 31.82417; 34.74667 السكان 1879 (1948) المساحة 18553 دونم تاريخ التهجير 13 مايو 1948 سبب التهجير هجوم عسكري من قبل قوات اليشوب بشيت، كانت قرية فلسطينية تقع في قضاء الرملة وتبعد من مركز المحافظة 16 كم ...

Bradley Zimmer

American baseball player (born 1992) Baseball player Bradley ZimmerZimmer with the Cleveland Indians in 2020Free agent Center fielderBorn: (1992-11-27) November 27, 1992 (age 31)San Diego, California, U.S.Bats: LeftThrows: RightMLB debutMay 16, 2017, for the Cleveland IndiansMLB statistics (through 2022 season)Batting average.213Home runs21Runs batted in91 Teams Cleveland Indians (2017–2021) Toronto Blue Jays (2022) Philadelphia Phillies (2022) Toronto Blue Jays (2022) B...

 

 

العلاقات الغانية الكينية

العلاقات الغانية الكينية غانا كينيا   غانا   كينيا تعديل مصدري - تعديل   العلاقات الغانية الكينية هي العلاقات الثنائية التي تجمع بين غانا وكينيا.[1][2][3][4][5] مقارنة بين البلدين هذه مقارنة عامة ومرجعية للدولتين: وجه المقارنة غانا كينيا المساح�...

 

 

The Assassin (film 2015)

The AssassinNama lainTionghoa刺客聶隱娘MandarinNièyǐnniáng SutradaraHou Hsiao-HsienDitulis oleh Hou Hsiao-Hsien Chu Tien-wen Hsieh Hai-Meng Zhong Acheng Pemeran Shu Qi Chang Chen Zhou Yun Satoshi Tsumabuki Penata musikLim GiongSinematograferMark Lee Ping BinPenyuntingHuang Chih-ChiaDistributorWell Go USA (Amerika Utara)StudioCanal (Britania Raya)[1]Tanggal rilis 21 Mei 2015 (2015-05-21) (Cannes) 27 Agustus 2015 (2015-08-27) (China, Hong Kong) 28 A...

Caning in Malaysia

Corporal punishmentPart of a series onCorporal punishment By place Domestic Judicial School By implementation Amputation Belting Birching Branding Caning Cat o' nine tails Flagellation Foot whipping Knout Paddle Scourge Sjambok Slippering Spanking Strapping Switch Tawse Riding crop Whip By country Afghanistan Brunei Iran Malaysia Qatar Singapore Taiwan United Arab Emirates United States Court cases CFCYL v. Canada Ingraham v. Wright S v Williams Tyrer v. the United Kingdom Politics Campaigns ...

 

 

أكرولين

[2] أكرولين أكرولين أكرولين أكرولين الاسم النظامي (IUPAC) Prop-2-enal أسماء أخرى Acraldehyde[1]Acrylic aldehyde[1]Allyl Aldehyde[1]Ethylene Aldehyde Acrylaldehyde[1] المعرفات رقم CAS 107-02-8 Y بوب كيم (PubChem) 7847 مواصفات الإدخال النصي المبسط للجزيئات O=CC=C C=CC=O المعرف الكيميائي الدولي 1S/C3H4O/c1-2-3-4/h2-3H,1H2 YKey:...

 

 

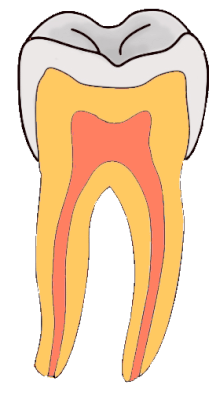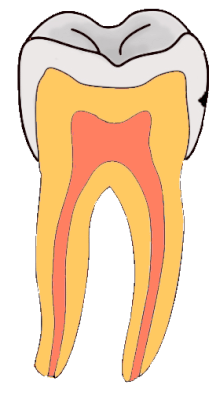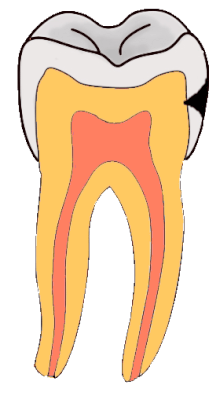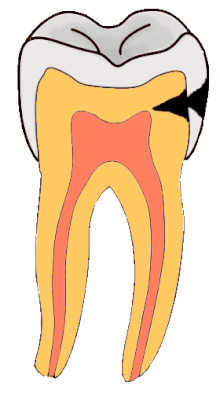
Geriatric dentistry

Geriatric DentistryAn elderly woman in a residential care home receiving dental treatmentSignificant diseasesDementia, arthritis, palliative care, osteoporosis, osteoarthritis, rheumatoid arthritis, Parkinson's disease, atherosclerosis, heart disease, high blood pressure, high cholesterolSpecialistDentist Geriatric dentistry is the delivery of dental care to older adults involving diagnosis, prevention, management and treatment of problems associated with age related diseases.[1] The ...

Battle of Toulon (1944)

Battle fought during WWII This article is about the Battle of Toulon in World War II. For other uses, see Battle of Toulon (disambiguation). Not to be confused with the Scuttling of the French fleet in Toulon in 1942. You can help expand this article with text translated from the corresponding article in French. (July 2015) Click [show] for important translation instructions. View a machine-translated version of the French article. Machine translation, like DeepL or Google Translate, is ...

 

 

ويسلي كلارك

يفتقر محتوى هذه المقالة إلى الاستشهاد بمصادر. فضلاً، ساهم في تطوير هذه المقالة من خلال إضافة مصادر موثوق بها. أي معلومات غير موثقة يمكن التشكيك بها وإزالتها. (نوفمبر 2023) تحتاج هذه المقالة إلى الاستشهاد بمصادر إضافية لتحسين وثوقيتها. فضلاً ساهم في تطوير هذه المقالة بإضافة اس...

 

 

Faltings's theorem

Curves of genus > 1 over the rationals have only finitely many rational points Faltings's theoremGerd FaltingsFieldArithmetic geometryConjectured byLouis MordellConjectured in1922First proof byGerd FaltingsFirst proof in1983GeneralizationsBombieri–Lang conjectureMordell–Lang conjectureConsequencesSiegel's theorem on integral points Faltings's theorem is a result in arithmetic geometry, according to which a curve of genus greater than 1 over the field Q {\displaystyle \mathbb {Q} } of r...

MAN SE

MAN Truck & Bus Deutschland GmbH Tipo PúblicaISIN DE0005937007 y DE0005937031Industria AutomovilísticaForma legal Societas EuropaeaFundación 1758 (266 años)Disolución 31 de agosto de 2021Sede central Múnich, AlemaniaÁrea de operación MundialProductos CamionesAutobusesMotoresCajas de cambiosTurbomaquinariaIngresos 15.772 millones de € (2012)[1]​Beneficio económico 964 millones de € (2012)Beneficio neto 189 millones de € (2012)Activos 19.918 millones de € (2012)P...

 

 

The Order Made

この記事には複数の問題があります。改善やノートページでの議論にご協力ください。 出典がまったく示されていないか不十分です。内容に関する文献や情報源が必要です。（2015年9月） 音楽の特筆性の基準を満たしていないおそれがあります。（2015年9月）出典検索?: The Order Made – ニュース · 書籍 · スカラー · CiNii · J-STAGE · NDL · d...