Математика в Стародавньому Єгипті
|
Read other articles:

Sebuah masjid Chin Haw di Doi Mae Salong, Chiang Rai Chin Haw, Chin Ho (Hanzi: 秦霍; Pinyin: Qín huò; bahasa Thai: จีนฮ่อ, RTGS: Chin Ho) atau Yunnan di Thailand (bahasa Thai: จีนยูนนาน) adalah orang Tionghoa yang bermigrasi ke Thailand melalui Myanmar atau Laos. Kebanyakan dari mereka berasal dari Yunnan, provinsi selatan Tiongkok.[1][2] Referensi ^ https://web.archive.org/web/20120220130034/http://khondoi.com/thai/index.php?o...

Artikel ini sebatang kara, artinya tidak ada artikel lain yang memiliki pranala balik ke halaman ini.Bantulah menambah pranala ke artikel ini dari artikel yang berhubungan atau coba peralatan pencari pranala.Tag ini diberikan pada Januari 2023. Bapalas Benua Bekasik adalah salah satu upacara adat yang yang dilaksanakan oleh masyarakat Dayak di Kalimantan. Upacara ini biasa dilakukan setelah masa panen selesai sebagai ungkapan rasa syukur karena Sang Pencipta telah memberikan rezeki dan anuger...

Musée du LouvreIstana LouvreLocation within Paris, PrancisDidirikan1793LokasiPalais Royal, Musée du Louvre,75001 Paris, PrancisJenisMuseum seni, museum desain/tekstil, situs bersejarahWisatawan8.3 juta (2007)[1]8.5 juta (2008)[2]8.5 juta (2009)[3]8.8 juta (2011)[4] Peringkat pertama nasional Peringkat pertama global DirekturHenri LoyretteKuratorMarie-Laure de RochebruneAkses transportasi umum Palais Royal – Musée du Louvre Louvre-Rivoli...

King of Babylon Marduk-šāpik-zēriKing of BabylonCylinder of Marduk-šāpik-zēri commemorating reconstruction of the Imgur-Enlil wall of Babylon.[i 1]Reignc. 1077–1065 BC[a]PredecessorMarduk-nadin-aḫḫēSuccessorAdad-apla-iddinaHouse2nd Dynasty of Isin Marduk-šāpik-zēri, inscribed in cuneiform dAMAR.UTU-DUB-NUMUN or phonetically -ša-pi-ik-ze-ri, and meaning “Marduk (is) the outpourer of seed”, reigned c. 1077–1065 BC, was the 7th king of the 2nd dynasty of Is...

Dalam nama Tionghoa ini, nama keluarganya adalah Chen. Chen Zaidao Chen Zaidao (Hanzi sederhana: 陈再道; Hanzi tradisional: 陳再道; Pinyin: Chén Zàidào, 1909–1993) adalah seorang jenderal Tiongkok dalam Tentara Pembebasan Rakyat, yang mengkomandani Kawasan Militer Wuhan dari 1954 sampai 1967. Ia dikenal karena menangkap tokoh pro-Mao Xie Fuzhi dan Wang Li dalam Insiden Wuhan pada Juli 1967.[1] Ia dipecat setelah insiden tersebut, tetapi direhabilitasi pada 1972 ...

Association football competition This article is about the all-Ireland association football competition. For other uses of the term, see Champions Cup. Football tournamentChampions CupOrganising bodyIrish Football AssociationFootball Association of IrelandFounded2019Region Northern Ireland Republic of IrelandNumber of teams2Current champions DundalkMost successful club(s) Dundalk (1 title)[1] The Champions Cup (known as the Unite the Union Champions Cup for sponsorship purposes) was a...

Mbark Boussoufa Pertandingan Iran-Maroko, Piala Dunia FIFA 2018Informasi pribadiNama lengkap Mbark BoussoufaTanggal lahir 15 Agustus 1984 (umur 39)Tempat lahir Amsterdam, BelandaTinggi 167 cm (5 ft 6 in)Posisi bermain GelandangInformasi klubKlub saat ini Al JaziraNomor 10Karier senior*Tahun Tim Tampil (Gol)2016 – Al Jazira 37 (7)Tim nasional2006 – Maroko 61 (7) * Penampilan dan gol di klub senior hanya dihitung dari liga domestik Mbark Boussoufa (lahir 15 Agustus 1984...

Cet article est une ébauche concernant une localité italienne et la Vénétie. Vous pouvez partager vos connaissances en l’améliorant (comment ?) selon les recommandations des projets correspondants. Consultez la liste des tâches à accomplir en page de discussion. Belluno Armoiries Drapeau Noms Nom français Bellune Administration Pays Italie Région Vénétie Province Belluno Maire Mandat Oscar De Pellegrin 2022-2027 Code postal 32100 Code ISTAT 025006 Code cadastral...

提示:此条目页的主题不是中華人民共和國最高領導人。 中华人民共和国 中华人民共和国政府与政治系列条目 执政党 中国共产党 党章、党旗党徽 主要负责人、领导核心 领导集体、民主集中制 意识形态、组织 以习近平同志为核心的党中央 两个维护、两个确立 全国代表大会 (二十大) 中央委员会 (二十届) 总书记:习近平 中央政治局 常务委员会 中央书记处 �...

本條目存在以下問題,請協助改善本條目或在討論頁針對議題發表看法。 此條目可参照英語維基百科相應條目来扩充。 (2022年12月23日)若您熟悉来源语言和主题,请协助参考外语维基百科扩充条目。请勿直接提交机械翻译,也不要翻译不可靠、低品质内容。依版权协议,译文需在编辑摘要注明来源,或于讨论页顶部标记{{Translated page}}标签。 此條目需要补充更多来源。 (2022年...
2020年夏季奥林匹克运动会波兰代表團波兰国旗IOC編碼POLNOC波蘭奧林匹克委員會網站olimpijski.pl(英文)(波兰文)2020年夏季奥林匹克运动会(東京)2021年7月23日至8月8日(受2019冠状病毒病疫情影响推迟,但仍保留原定名称)運動員206參賽項目24个大项旗手开幕式:帕维尔·科热尼奥夫斯基(游泳)和马娅·沃什乔夫斯卡(自行车)[1]闭幕式:卡罗利娜·纳亚(皮划艇)&#...

Dewan Perwakilan Rakyat Daerah Kabupaten LuwuDewan Perwakilan RakyatKabupaten Luwu2019–2024JenisJenisUnikameral Jangka waktu5 tahunSejarahSesi baru dimulai2 September 2019PimpinanKetuaRusli Sunali, S.Pd. (PPP) sejak 9 Oktober 2019 Wakil Ketua IMappatunru (Perindo) sejak 9 Oktober 2019 Wakil Ketua IIZulkifli, S.T., M.Si. (Golkar) sejak 12 Desember 2019 KomposisiAnggota35Partai & kursi PDI-P (3) NasDem (3) PKB (2) Hanura (1) ...

Product of rock weathering in wet tropical climates rich in iron and aluminium Traditional laterite temple in Kerala Monument of laterite brickstones at Angadipuram, Kerala, India, which commemorates where laterite was first described and discussed by Buchanan-Hamilton in 1807 Laterite is a soil type rich in iron and aluminium and is commonly considered to have formed in hot and wet tropical areas. Nearly all laterites are of rusty-red coloration, because of high iron oxide content. They deve...

British colonial official (1781–1826) This article needs additional citations for verification. Please help improve this article by adding citations to reliable sources. Unsourced material may be challenged and removed.Find sources: Stamford Raffles – news · newspapers · books · scholar · JSTOR (September 2023) (Learn how and when to remove this message) The Honourable SirStamford RafflesFRSPortrait by George Francis Joseph, c. 1817Lieutenant-Governo...

Rural municipality in Manitoba, Canada This article is about the rural municipality. For the city, see Thompson, Manitoba. Rural municipality in Manitoba, CanadaRural Municipality of ThompsonRural municipalityMiami Railway StationLocation of the RM of Thompson in ManitobaCoordinates: 49°22′37″N 98°14′21″W / 49.37694°N 98.23917°W / 49.37694; -98.23917CountryCanadaProvinceManitobaArea • Land531.24 km2 (205.11 sq mi)Population (...

Disambiguazione – MES e Mes rimandano qui. Se stai cercando altri significati, vedi Mes (disambigua). Meccanismo europeo di stabilità(DE) Europäischer Stabilitätsmechanismus(EN) European Stability Mechanism(ES) Mecanismo Europeo de Estabilidad(FR) Mécanisme européen de stabilité In blu, i Paesi membri del MES Fondazione25 marzo 2011 Sede centrale Lussemburgo (città) PresidentePierre Gramegna Sito web Modifica dati su Wikidata · Manuale Il Meccanismo europeo di stabilit...

War between the Byzantine Empire and the First Bulgarian Empire Byzantine–Bulgarian war of 913–927Part of the Byzantine–Bulgarian warsBulgarian–Serbian warsDate913–927LocationBalkan PeninsulaResult Bulgarian victory Byzantium recognizes the imperial title of the Bulgarian monarchs and the Bulgarian PatriarchateTerritorialchanges Serbia annexed by BulgariaBelligerents Bulgarian Empire Byzantine Empire Principality of Serbia Commanders and leaders Simeon I the Great Peter I George Sur...
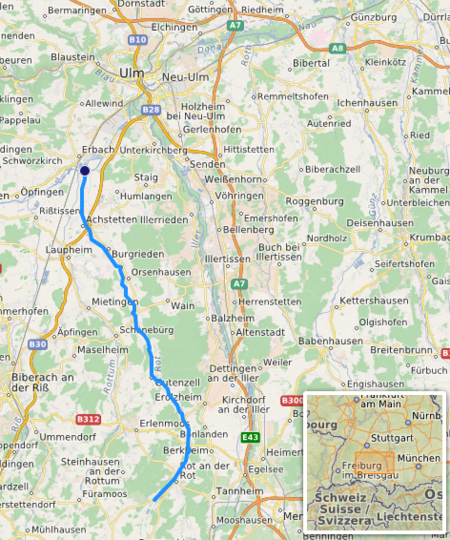
River in Germany RotLocationCountryGermanyStateBaden-WürttembergPhysical characteristicsSource • locationnear Rot an der Rot Mouth • locationDanube • coordinates48°18′47″N 9°54′0″E / 48.31306°N 9.90000°E / 48.31306; 9.90000Length55.8 km (34.7 mi) [1]Basin size297 km2 (115 sq mi) [1]Discharge • average10 m3/s (350 cu ...

Questa voce o sezione sull'argomento drammi non cita le fonti necessarie o quelle presenti sono insufficienti. Puoi migliorare questa voce aggiungendo citazioni da fonti attendibili secondo le linee guida sull'uso delle fonti. Così è (se vi pare)Opera teatrale in 3 atti Luigi Pirandello nel 1932 AutoreLuigi Pirandello Lingua originaleItaliano Generedramma Composto nel1917 Prima assoluta18 giugno 1917Teatro Olimpia, Milano Personaggi Lamberto Laudisi La Signora Frola Il Signor Ponza, s...

春日 由三(かすが よしかず、1911年(明治44年)11月10日[1] - 1995年(平成7年)10月22日[2])は、日本の政治家。新潟県十日町市長(2期)。日本民謡協会理事長[2]。NHK専務理事。 経歴 現在の新潟県十日町市出身。大島三五郎の三男に生まれ、春日家の養子となる[1]。1935年に東京帝国大学法学部法律学科を卒業[1][2]。同年、NHKに入局[1&...

















