Комбінаторика многогранників
|
Read other articles:

Artikel ini sebatang kara, artinya tidak ada artikel lain yang memiliki pranala balik ke halaman ini.Bantulah menambah pranala ke artikel ini dari artikel yang berhubungan atau coba peralatan pencari pranala.Tag ini diberikan pada Februari 2023. Drypetes Drypetes deplanchei (en) TaksonomiDivisiTracheophytaSubdivisiSpermatophytesKladAngiospermaeKladmesangiospermsKladeudicotsKladcore eudicotsKladSuperrosidaeKladrosidsKladfabidsOrdoMalpighialesFamiliPutranjivaceaeGenusDrypetes Vahl, 1807 Tata na...

Galeazzo Ciano Menteri Urusan Luar Negeri ItaliaMasa jabatan9 Juni 1936 – 6 Februari 1943Penguasa monarkiVictor Emmanuel IIIRaja ItaliaPerdana MenteriBenito Mussolini PendahuluBenito MussoliniPenggantiBenito Mussolini Informasi pribadiLahirGian Galeazzo Ciano(1903-03-18)18 Maret 1903Livorno, Toskana, ItaliaMeninggal11 Januari 1944(1944-01-11) (umur 40)Verona, Republik Sosial ItaliaPartai politikPartai Fasis Nasional (PFN)Suami/istriEdda Mussolini Ciano (1910-1944)AnakFabrizio ...

Spanish footballer Not to be confused with Tomas Piñas. In this Spanish name, the first or paternal surname is Pina and the second or maternal family name is Isla. Tomás Pina Pina in action for Mallorca in 2012Personal informationFull name Tomás Pina Isla[1]Date of birth (1987-10-14) 14 October 1987 (age 36)[1]Place of birth Villarta de San Juan, SpainHeight 1.84 m (6 ft 0 in)[1]Position(s) MidfielderTeam informationCurrent team MurciaNum...
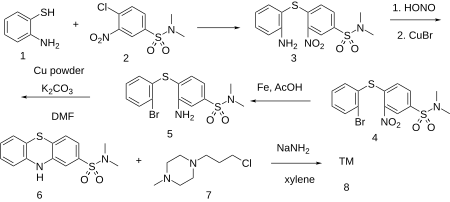
Typical antipsychotic medication ThioproperazineClinical dataTrade namesMajeptilATC codeN05AB08 (WHO) Legal statusLegal status BR: Class C1 (Other controlled substances)[1] Identifiers IUPAC name N,N-dimethyl-10-[3-(4-methylpiperazin-1-yl)propyl]-10H-phenothiazine-2-carboxamide CAS Number316-81-4PubChem CID9429DrugBankDB01622ChemSpider9058UNIIYJ050AQ56XKEGGD08585ChEBICHEBI:59120ChEMBLChEMBL609109CompTox Dashboard (EPA)DTXSID1023655 ECHA InfoCard100.005.695 Chemical and ...

Badan Geologi Kementerian Energi dan Sumber Daya MineralRepublik IndonesiaLogo Kementerian ESDMGambaran umumDibentuk1850Nomenklatur sebelumnyaDienst van het MijnwezenPusat Penelitian dan Pengembangan GeologiBidang tugasGeologiSloganGeologi untuk Perlindungan dan Kesejahteraan MasyarakatSusunan organisasiKepala BadanEko Budi LelonoSekretaris BadanEdiar Usman Kepala PusatSumber Daya Mineral, Batubara, dan Panas BumiIman Kristian SinulinggaVulkanologi dan Mitigasi Bencana GeologiAndianiAir Tanah...

Three Ravinia Drive in 2017 Three Ravinia Drive is a skyscraper located in the city of Dunwoody, in metropolitan Atlanta. Standing 31 stories and 444 feet (135 meters) tall, it is the tallest building in Dunwoody. Ravinia was developed by Gerald Hines Interests of Houston, Texas, in 1991. It is part of a large business complex that includes the twin 17-story towers of One and Two Ravinia Drive, a 15-story Crowne Plaza Hotel and a park.[1] The tower is used mostly for commercial office...

Bandar Udara Internasional Phuketท่าอากาศยานภูเก็ตIATA: HKTICAO: VTSPInformasiJenisPublikPemilik/PengelolaAirports of Thailand PCL (AOT)MelayaniPhuketLokasi222 Mai Khao, Thalang, Phuket, ThailandMaskapai utamaNok AirThai Airways InternationalKetinggian dpl mdplKoordinat08°06′47″N 098°19′00″E / 8.11306°N 98.31667°E / 8.11306; 98.31667Koordinat: 08°06′47″N 098°19′00″E / 8.11306°N 98.31667�...

Peta yang menunjukkan letak Buruanga. Buruanga adalah munisipalitas di provinsi Aklan, Filipina. Pada tahun 2011, wilayah ini memiliki penduduk sebanyak 15.767 jiwa atau 3.204 rumah tangga.[1] Pembagian wilayah Secara administratif Buruanga terbagi atas 15 barangay, yaitu: Alegria Bagongbayan Balusbos Bel-is Cabugan El Progreso Habana Katipunan Mayapay Nazareth Panilongan Poblacion Santander Tag-osip Tigum Referensi ^ Local Governance Performance Management System[pranala nonaktif...

† Человек прямоходящий Научная классификация Домен:ЭукариотыЦарство:ЖивотныеПодцарство:ЭуметазоиБез ранга:Двусторонне-симметричныеБез ранга:ВторичноротыеТип:ХордовыеПодтип:ПозвоночныеИнфратип:ЧелюстноротыеНадкласс:ЧетвероногиеКлада:АмниотыКлада:Синапсиды�...

The Element of Freedom Album de Alicia Keys Sortie 15 décembre 2009 11 décembre 2009 Enregistré Mai - Septembre 2009The Oven StudiosLong Island, New York Durée 52:24 Genre Neo soul, R'n'B, pop, soft rock Auteur Alicia Keys, Patrick « Plan Pat » Reynolds, Drake Compositeur Jeff BhaskerKasseem DeanNoah « 40 » ShebibAl Shux Producteur Alicia KeysKerry « Krucial » BrothersPeter Edge Label J Records / MBK Critique AllMusic [1]Independent [2]Rolling Sto...

Las EstrellasJenisJaringan televisi terestrialSloganCon las estrellas.(Dengan bintang-bintang)Negara MeksikoKetersediaanMeksikoEropa: Canal de las Estrellas EuropaAmerika Latin: Canal de las Estrellas LatinoamericaTanggal peluncuran1951PemilikTelevisaSitus webLas Estrellas Las Estrellas (Bintang-bintang) adalah salah satu jaringan televisi utama dari Televisa yang memiliki stasiun-stasiun afiliasi di seluruh Meksiko, dengan stasiun televisi utamanya, XEW-TV di Mexico City. Sebagian dari ...

此條目可参照英語維基百科相應條目来扩充。 (2021年5月6日)若您熟悉来源语言和主题,请协助参考外语维基百科扩充条目。请勿直接提交机械翻译,也不要翻译不可靠、低品质内容。依版权协议,译文需在编辑摘要注明来源,或于讨论页顶部标记{{Translated page}}标签。 约翰斯顿环礁Kalama Atoll 美國本土外小島嶼 Johnston Atoll 旗幟颂歌:《星條旗》The Star-Spangled Banner約翰斯頓環礁�...

Village in Republika Srpska, Bosnia and HerzegovinaJošavka GornjaVillageJošavka GornjaShow map of Republika SrpskaJošavka GornjaShow map of Bosnia and HerzegovinaCoordinates: 44°43′N 17°28′E / 44.717°N 17.467°E / 44.717; 17.467CountryBosnia and HerzegovinaEntityRepublika SrpskaMunicipalityČelinacTime zoneUTC+1 (CET) • Summer (DST)UTC+2 (CEST) Jošavka Gornja (Cyrillic: Јошавка Горња) is a village in the municipality of Čelinac, Repu...

American film production studio, financer and international distributor QED InternationalLogo used since the 2002Company typePrivateIndustry Motion pictures Business media Publishing Founded2002; 22 years ago (2002)FounderBill BlockHeadquartersLos Angeles, California, United StatesArea servedWorldwideKey peopleSasha Shapiro (CEO)Anton LessineProducts Filmmaking Film Production ServicesFinancingParentMedia Content Capital (2012 - present)Websiteqedinternational.com QED Intern...

Lake in Wuhan, China This article needs additional citations for verification. Please help improve this article by adding citations to reliable sources. Unsourced material may be challenged and removed.Find sources: East Lake Wuhan – news · newspapers · books · scholar · JSTOR (April 2010) (Learn how and when to remove this message) East LakeDong Hu东湖 (Chinese)East LakeShow map of ChinaEast LakeShow map of HubeiLocationWuchang District an...

Lee Metcalf WildernessIUCN category Ib (wilderness area)Show map of the United StatesShow map of MontanaLocationMadison / Gallatin counties, Montana, USANearest cityBozeman, MTCoordinates45°08′N 111°27′W / 45.133°N 111.450°W / 45.133; -111.450Area254,288 acres (1,029.07 km2)Established1983Governing bodyU.S. Forest ServiceU.S. Bureau of Land Management The Lee Metcalf Wilderness is located in the northern Rocky Mountains in the U.S. state of Monta...

American ice hockey forward (born 1989) Ice hockey player Jocelyne Lamoureux Jocelyne Lamoureux playing for Team USA against the ECAC All-Stars in 2010Born (1989-07-03) July 3, 1989 (age 34)Grand Forks, North Dakota, U.S.Height 5 ft 6 in (168 cm)Weight 154 lb (70 kg; 11 st 0 lb)Position ForwardShot RightPlayed for University of MinnesotaUniversity of North DakotaNational team United StatesPlaying career 2008–2021 Medal record Olympic Games 2...

Ruined city located in Düzce Province, Turkey Prusias ad HypiumKonuralpStone fragments at Prusias ad Hypium ruins.Shown within TurkeyLocationTurkeyRegionDüzce ProvinceCoordinates40°54′22″N 31°08′53″E / 40.90611°N 31.14806°E / 40.90611; 31.14806TypeSettlementHistoryPeriodsHellenistic, Roman, Byzantine, OttomanSite notesPublic accessLimited Wikimedia Commons has media related to Prusias ad Hypium. Prusias ad Hypium (Ancient Greek: Προῦσα πρὸ...

American manufacturing company For the Australian entertainment company, see Crown Resorts. For the American cable network operator, see Crown Media. Crown Holdings, Inc.Brand-Building PackagingCompany typePublic companyTraded asNYSE: CCKS&P 400 componentIndustryPackagingFounded1892; 132 years ago (1892)FounderWilliam PainterHeadquartersYardley, Pennsylvania, U.S.Key peopleTimothy J. Donahue(CEO, President, and Chairman of the Board)Kevin C. Clothier(CFO and SVP)Pro...

American politician (1833–1910) For the United States federal judge, see Thomas Collier Platt Jr. For his political organization, see Platt machine. Thomas C. PlattPlatt in 1903United States Senatorfrom New YorkIn officeMarch 4, 1897 – March 3, 1909Preceded byDavid B. HillSucceeded byElihu RootIn officeMarch 4, 1881 – May 16, 1881Preceded byFrancis KernanSucceeded byWarner MillerMember of theU.S. House of Representativesfrom New YorkIn officeMarch 4, 1873 – ...


