Векторне розшарування
|
Read other articles:

Artikel ini membutuhkan rujukan tambahan agar kualitasnya dapat dipastikan. Mohon bantu kami mengembangkan artikel ini dengan cara menambahkan rujukan ke sumber tepercaya. Pernyataan tak bersumber bisa saja dipertentangkan dan dihapus.Cari sumber: Prasasti Anjuk Ladang – berita · surat kabar · buku · cendekiawan · JSTOR Prasasti Anjuk Ladang di Museum Nasional Jakarta. Prasasti Anjuk Ladang adalah piagam batu berangka tahun 859 Saka (versi L.-C. Damais...

US online nonprofit news outlet For other uses, see Intercept (disambiguation). The InterceptScreenshot Type of siteNews websiteAvailable inEnglishPortugueseURLtheintercept.com CommercialNoLaunchedFebruary 2014 Photograph by Trevor Paglen of the National Security Agency headquarters in Fort Meade first published in The Intercept The Intercept is an online American nonprofit news organization that publishes articles and podcasts. The Intercept has published in English since its founding i...

1969 documentary film about life in Nazi-occupied France This article has multiple issues. Please help improve it or discuss these issues on the talk page. (Learn how and when to remove these template messages) You can help expand this article with text translated from the corresponding article in French. (November 2018) Click [show] for important translation instructions. View a machine-translated version of the French article. Machine translation, like DeepL or Google Translate, is a u...

Vysšaja Liga 1975высшая лига 1975 Competizione Vysšaja Liga Sport Calcio Edizione 38ª Organizzatore FFSSSR Date dal 12 aprile 1975al 16 novembre 1975 Luogo Unione Sovietica Partecipanti 16 Formula Girone all'italiana Risultati Vincitore Dinamo Kiev(7º titolo) Retrocessioni PaxtakorSKA Rostov Statistiche Miglior marcatore Blochin (18) Incontri disputati 240 Gol segnati 544 (2,27 per incontro) Cronologia della competizione 1974 primavera 1976 Manuale L'edi...

This article includes a list of references, related reading, or external links, but its sources remain unclear because it lacks inline citations. Please help improve this article by introducing more precise citations. (June 2013) (Learn how and when to remove this message) 1968 Dodge K, originally sold as the 500 The Dodge 500 was a heavy duty truck introduced in 1964 and built in the United Kingdom by Dodge. It replaced Dodge UK's earlier 300 series cab over trucks. History and development ...

Daniel Nicholas DiNardoKardinal, Uskup Agung Galveston-HoustonKeuskupan agungGalveston-HoustonPenunjukan16 Januari 2004 (Uskup Koadjutor)29 Desember 2004 (Coadjutor Archbishop)Awal masa jabatan26 Maret 2004 (Uskup Koadjutor)28 Februari 2006 (Uskup Agung)PendahuluJoseph FiorenzaJabatan lainKardinal-Imam S. EusebioAnggota Sekretariat bagi EkonomiPresiden Konferensi Waligereja Amerika SerikatImamatTahbisan imam16 Juli 1977oleh Vincent Martin LeonardTahbisan uskup7 Oktober 1997oleh Lawr...

Chronologies Données clés 1576 1577 1578 1579 1580 1581 1582Décennies :1540 1550 1560 1570 1580 1590 1600Siècles :XIVe XVe XVIe XVIIe XVIIIeMillénaires :-Ier Ier IIe IIIe Chronologies thématiques Art Architecture, Arts plastiques (Dessin, Gravure, Peinture et Sculpture), (), Littérature () et Musique (Classique) Ingénierie (), Architecture et () Politique Droit Religion (,) Science () et Santé...

Pattern in a crop field Crop circles redirects here. For other uses, see Crop circles (disambiguation). For the irrigation method that produces circular fields of crops, see center pivot irrigation. Aerial view of crop circles in Switzerland A crop circle, crop formation, or corn circle is a pattern created by flattening a crop,[1] usually a cereal. The term was first coined in the early 1980s by Colin Andrews.[2] Crop circles have been described as all falling within the rang...

この項目には、一部のコンピュータや閲覧ソフトで表示できない文字が含まれています(詳細)。 数字の大字(だいじ)は、漢数字の一種。通常用いる単純な字形の漢数字(小字)の代わりに同じ音の別の漢字を用いるものである。 概要 壱万円日本銀行券(「壱」が大字) 弐千円日本銀行券(「弐」が大字) 漢数字には「一」「二」「三」と続く小字と、「壱」「�...

この項目には、一部のコンピュータや閲覧ソフトで表示できない文字が含まれています(詳細)。 数字の大字(だいじ)は、漢数字の一種。通常用いる単純な字形の漢数字(小字)の代わりに同じ音の別の漢字を用いるものである。 概要 壱万円日本銀行券(「壱」が大字) 弐千円日本銀行券(「弐」が大字) 漢数字には「一」「二」「三」と続く小字と、「壱」「�...

هذه المقالة يتيمة إذ تصل إليها مقالات أخرى قليلة جدًا. فضلًا، ساعد بإضافة وصلة إليها في مقالات متعلقة بها. (مارس 2023) تحتاج هذه المقالة إلى الاستشهاد بمصادر إضافية لتحسين وثوقيتها. فضلاً ساهم في تطوير هذه المقالة بإضافة استشهادات من مصادر موثوق بها. من الممكن التشكيك بالمعلو...

American judge (born 1977) Dale HoJudge of the United States District Court for the Southern District of New YorkIncumbentAssumed office August 18, 2023Appointed byJoe BidenPreceded byKatherine B. Forrest Personal detailsBornDale Edwin Ho[1]1977 (age 46–47)San Jose, California, U.S.EducationPrinceton University (BA)Yale University (JD) Dale Ho's voice Dale Ho's opening statements to the Supreme Court in Department of Commerce v. New YorkRecorded April 23, 2019 Dale Edw...

本表是動態列表,或許永遠不會完結。歡迎您參考可靠來源來查漏補缺。 潛伏於中華民國國軍中的中共間諜列表收錄根據公開資料來源,曾潛伏於中華民國國軍、被中國共產黨聲稱或承認,或者遭中華民國政府調查審判,為中華人民共和國和中國人民解放軍進行間諜行為的人物。以下列表以現今可查知時間為準,正確的間諜活動或洩漏機密時間可能早於或晚於以下所歸�...

American football player (born 1984) American football player Alan BranchBranch with the New England Patriots in 2015No. 78, 99, 97, 90Position:Defensive tacklePersonal informationBorn: (1984-12-29) December 29, 1984 (age 39)Rio Rancho, New Mexico, U.S.Height:6 ft 6 in (1.98 m)Weight:350 lb (159 kg)Career informationHigh school:Cibola(Albuquerque, New Mexico)College:Michigan (2004–2006)NFL draft:2007 / Round: 2 / Pick: 33Career history Arizo...

Questa voce sull'argomento cestisti spagnoli è solo un abbozzo. Contribuisci a migliorarla secondo le convenzioni di Wikipedia. Segui i suggerimenti del progetto di riferimento. Blanca AresNazionalità Spagna Altezza180 cm Pallacanestro RuoloAla CarrieraSquadre di club P.B. Godella Nazionale 1989 Spagna U-191988-1994 Spagna124 (1.754) Palmarès Europei OroItalia 1993 Giochi del Mediterraneo OroAtene 1991 BronzoLinguadoca-Rossiglione 1993 Universiadi Argento...

Volcanic region hotter than the surrounding mantle Diagram showing a cross section through Earth at the Hawaii hotspot. Magma originating in the mantle rises into the asthenosphere and lithosphere. A chain of volcanoes is created as the lithosphere moves over the source of magma. In geology, hotspots (or hot spots) are volcanic locales thought to be fed by underlying mantle that is anomalously hot compared with the surrounding mantle.[1] Examples include the Hawaii, Iceland, and Yello...

Cyrillic letter Cyrillic letterChe with diaeresisPhonetic usage:/tʃ/The Cyrillic scriptSlavic lettersАА̀А̂А̄ӒБВГҐДЂЃЕЀЕ̄Е̂ЁЄЖЗЗ́ЅИІЇꙆЍИ̂ӢЙЈКЛЉМНЊОО̀О̂ŌӦПРСС́ТЋЌУУ̀У̂ӮЎӰФХЦЧЏШЩꙎЪЪ̀ЫЬѢЭЮЮ̀ЯЯ̀Non-Slavic lettersӐА̊А̃Ӓ̄ӔӘӘ́Ә̃ӚВ̌ԜГ̑Г̇Г̣Г̌Г̂Г̆Г̈г̊ҔҒӺҒ̌ғ̊ӶД́Д̌Д̈Д̣Д̆ӖЕ̃Ё̄Є̈ԐԐ̈ҖӜӁЖ̣ҘӞЗ̌З̣З̆ӠИ̃ӤҊҚӃҠҞҜК̣к̊қ̊ԚᴫЛ́ӅԮԒЛ̈...
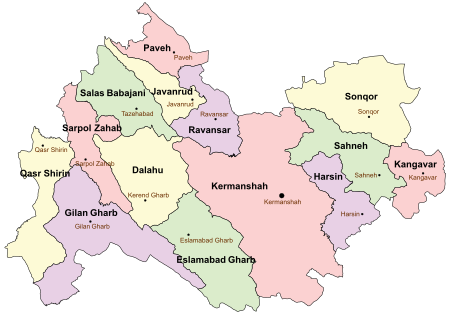
Province of Iran Not to be confused with Kermanshah County.For the city, see Kermanshah. Province in 4th Region, IranKermanshah Province Persian: استان کرمانشاهProvinceLocation of Kermanshah Province within IranCoordinates: 34°33′N 46°43′E / 34.550°N 46.717°E / 34.550; 46.717[1]CountryIranRegion4th RegionCapitalKermanshahCounties14Government • Governor-generalMohammad-Tayyeb Sahraee • MPs of Assembly of ExpertsAman N...

Questa voce sull'argomento calciatori cileni è solo un abbozzo. Contribuisci a migliorarla secondo le convenzioni di Wikipedia. Segui i suggerimenti del progetto di riferimento. Alejandro CarrascoNazionalità Cile Altezza174 cm Peso70 kg Calcio RuoloCentrocampista Termine carriera2016 CarrieraGiovanili 1994-1995 Audax Italiano Squadre di club1 1996-2003 Audax Italiano? (?)2003 Skoda Xanthī? (?)2004 Audax Italiano? (?)2005 Colo-Colo? (?)2005 Dep. Meli...

2006 film My Little Pony Crystal Princess: The Runaway RainbowDVD Cover for My Little Pony Crystal Princess: The Runaway RainbowDirected byJohn GrusdWritten byJeanne RomanoBased onMy Little Pony by Bonnie ZacherleProduced byJonathan DernStarringCathy WeseluckJanyse JaudVenus TerzoTabitha St. GermainAndrea LibmanChantal StrandBritt McKillipBrian DrummondKathleen BarrKelly SheridanAdrienne CarterTracey MooreMaryke HendrikseBrittney WilsonMusic byMark WattersTerry Sampson (songs)Productioncompan...



































