Бінгамівський пластик
|
Read other articles:

Goslar Lambang kebesaranLetak Goslar di Goslar NegaraJermanNegara bagianNiedersachsenKreisGoslarSubdivisions18 distrikPemerintahan • Lord MayorDr Oliver Junk[1][2] (CDU)Luas • Total163,71 km2 (6,321 sq mi)Ketinggian255 m (837 ft)Populasi (2013-12-31)[3] • Total50.681 • Kepadatan3,1/km2 (8,0/sq mi)Zona waktuWET/WMPET (UTC+1/+2)Kode pos38640, 38642, 38644Kode area telepon05321, 05325Pelat ...

Indonesianis merujuk kepada tokoh-tokoh yang umumnya berkewarganegaraan asing, tetapi memiliki ketertarikan secara umum terhadap Indonesia atau melakukan kegiatan penelitian mengenai kebudayaan, politik dan kehidupan sosial di Indonesia. Beberapa Indonesianis antara lain: Nama Kewarganegaraan Anthony Reid Benedict Anderson Berthold Damshäuser Daniel S. Lev Dave McRae[1] Gerrit Jan Held George McTurnan Kahin Greg Acciaioli[2] Harold Crouch Henk Schulte Nordholt[3] Herb...

Persembahan seorang janda miskin (Inggris: The Widow's Mitecode: en is deprecated [1]) adalah suatu pelajaran yang dicatat dalam Injil Sinoptik (Markus 12:41–44, Lukas 21:1–4), pada waktu Yesus mengajar di Bait Allah di Yerusalem. Injil Markus menunjukkan bahwa dua peser (bahasa Yunani: lepton; bentuk jamak: lepta) bersama-sama bernilai satu duit (bahasa Yunani: quadrans), koin Romawi terkecil. Sebuah lepton adalah koin yang terkecil dan paling tidak berharga di antara koin yang b...

Stand Up Comedy Indonesia Kompas TVStand Up Comedy IndonesiaPembuatIndra Yudhistira Pandji Pragiwaksono Raditya Dika Indro WarkopPresenterPandji Pragiwaksono (2011-2015) Raditya Dika (2011) Ryan Adriandhy (2012) Ge Pamungkas (2013) Ernest Prakasa (2014) Babe Cabiita (2014-2016) Uus (2014-2016, 2021) David Nurbianto (2015-2016) Hifdzi Khoir (2015-2018, 2022-sekarang) Rigen (2016, 2021-sekarang) Gita Bhebhita (2017) Bianca Liza (2018) Yuki Kato (2021) Ananta Rispo (2022-sekarang)JuriIndro Wark...

Pour les articles homonymes, voir Johnny et Logan. Johnny Logan Johnny Logan en 2009.Informations générales Surnom Mister Eurovision Nom de naissance Seán Patrick Michael Sherrard Naissance 13 mai 1954 (69 ans)Frankston, Victoria, Australie Nationalité Irlandais Activité principale Chanteur, auteur-compositeur-interprète Genre musical Pop Instruments Chant Années actives 1978- Labels My Way MusicSony Music Entertainment GmbH Site officiel www.johnnylogan.com modifier Seán Sherra...

Cet article est une ébauche concernant le Bas-Rhin et le climat. Vous pouvez partager vos connaissances en l’améliorant (comment ?) selon les recommandations des projets correspondants. Chasse-neige à Strasbourg, en hiver. Le climat du Bas-Rhin est de type océanique à semi-continental, marqué par des hivers froids et secs et des étés chauds et orageux, du fait de la protection occidentale qu'offrent les Vosges. La température moyenne annuelle est de 10,4 °C en plaine (E...

Dalam nama Tionghoa ini, nama keluarganya adalah Chen. Chen Zaidao Chen Zaidao (Hanzi sederhana: 陈再道; Hanzi tradisional: 陳再道; Pinyin: Chén Zàidào, 1909–1993) adalah seorang jenderal Tiongkok dalam Tentara Pembebasan Rakyat, yang mengkomandani Kawasan Militer Wuhan dari 1954 sampai 1967. Ia dikenal karena menangkap tokoh pro-Mao Xie Fuzhi dan Wang Li dalam Insiden Wuhan pada Juli 1967.[1] Ia dipecat setelah insiden tersebut, tetapi direhabilitasi pada 1972 ...

Confederate Army general (1814–1875) For the American sugar industry executive, see Henry Arthur Benning. Henry L. BenningPortrait of Gen. Henry Lewis Benning by Bjorn EgeliBirth nameHenry Lewis BenningNickname(s)Old RockBorn(1814-04-02)April 2, 1814Columbia County, Georgia, U.S.DiedJuly 10, 1875(1875-07-10) (aged 61)Columbus, Georgia, U.S.BuriedLinwood CemeteryColumbus, Georgia, U.S.AllegianceConfederate States of AmericaService/branchConfederate States ArmyYears of service1861�...

Fluroxypyr Names Preferred IUPAC name [(4-Amino-3,5-dichloro-6-fluoropyridin-2-yl)oxy]acetic acid Identifiers CAS Number 69377-81-7 Y81406-37-3 (1-Methylheptyl ester) Y 3D model (JSmol) Interactive image ChEBI CHEBI:82017 Y ChemSpider 45757 ECHA InfoCard 100.126.253 PubChem CID 50465 UNII 8O40SHO197 Y9W47M4YJ3Q (1-Methylheptyl ester) Y CompTox Dashboard (EPA) DTXSID2034627 InChI InChI=1S/C7H5Cl2FN2O3/c8-3-5(11)4(9)7(12-6(3)10)15-1-2(13)14/h1H2,(H2,11,12)(H,...

Fictional character from The Godfather series For the Italian conductor, see Carlo Rizzi (conductor). Fictional character Carlo RizziGianni Russo as Carlo RizziFirst appearanceThe GodfatherLast appearanceThe Godfather Part II (flashback cameo)Created byMario PuzoPortrayed byGianni RussoIn-universe informationGenderMaleFamilyCorleone familySpouseConnie Corleone (1945–1955)ChildrenVictorMichael Francis Carlo Rizzi is a fictional character in Mario Puzo's 1969 novel The Godfather. In the 1972 ...

2020 studio album by Got7 Breath of Love: Last PieceDigital coverStudio album by Got7ReleasedNovember 30, 2020Recorded2020StudioJYPE StudiosVibe Music Studio 606GenreK-pop[1]Hip hop[1]R&B[1]Dance[1]Length32:39LanguageKoreanLabelJYPProducerJackson WangJoo Chan-yangLavinNathanZaysonRoseInPeaceEarattackGong-doBoytoyLudwig LindellPsycho TensionRalzLaconicArcadesGot7 chronology Dye(2020) Breath of Love: Last Piece(2020) Got7(2022) Singles from Breath of Love...
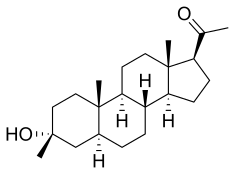
Chemical compound This scientific article needs additional citations to secondary or tertiary sources. Help add sources such as review articles, monographs, or textbooks. Please also establish the relevance for any primary research articles cited. Unsourced or poorly sourced material may be challenged and removed. (May 2017) (Learn how and when to remove this message) GanaxoloneClinical dataTrade namesZtalmyOther namesGNX; CCD-1042; 3β-Methyl-5α-pregnan-3α-ol-20-one; 3α-Hydroxy-3β-methyl...

Frederick Funston HenryLahir(1919-09-23)23 September 1919Vian, OklahomaMeninggal1 September 1950(1950-09-01) (umur 30)Naktong Bulge, dekat Andong, KoreaTempat pemakamanNational Memorial Cemetery of the PacificPengabdianAmerika SerikatDinas/cabangAngkatan Darat Amerika SerikatLama dinas1940 - 1950PangkatLetnan SatuKesatuanResimen Infanteri ke-38, Divisi Infanteri ke-2Perang/pertempuranPerang Dunia II Perang Korea Pertempuran Perimeter Pusan Pertempuran Naktong Bulge Kedua † Pe...

Radio station in Sioux Falls, South Dakota This article needs additional citations for verification. Please help improve this article by adding citations to reliable sources. Unsourced material may be challenged and removed.Find sources: KSOO AM – news · newspapers · books · scholar · JSTOR (July 2017) (Learn how and when to remove this message) KSOOSioux Falls, South DakotaFrequency1000 kHzBrandingESPN Sioux FallsProgrammingFormatSportsAffiliatio...

Bad Guys 2Poster promosiJudul asli나쁜 녀석들: 악의 도시 GenreProsedur kepolisianKriminalThrillerLagaPembuatStudio DragonDitulis olehHan Jung-hoonSutradaraHan Dong-hwaPemeranPark Joong-hoonJoo Jin-moYang Ik-juneKim Mu-yeolJi SooNegara asalKorea SelatanBahasa asliKoreaJmlh. episode16ProduksiProduser eksekutifHeo GunPengaturan kameraSingle cameraDurasi60Rumah produksiUrban Works MediaRilis asliFormat gambar1080i (HDTV)Format audioDolby DigitalRilis16 Desember 2017 (2017-12-16)Aca...

1948 murder in New Delhi, India Assassination of Gandhi redirects here. For other uses, see Assassination of Indira Gandhi and Assassination of Rajiv Gandhi. Assassination of Mahatma GandhiA memorial marks the spot in Birla House (now Gandhi Smriti), New Delhi, where Mahatma Gandhi was assassinated at 5:17 PM on 30 January 1948.LocationNew Delhi, IndiaDate30 January 1948 17:17 (IST)TargetMahatma GandhiAttack typeAssassination, murder by shootingWeaponsBeretta M 1934 semi-automatic pistolDeath...

Pour les articles homonymes, voir JTF (homonymie). Les navires du groupe de travail 100.1 participent à l'exercice OTAN BALTOPS en octobre 1985. En tête se trouvent les frégates ouest-allemandes Rheinland-Pfalz (F 209), à gauche, et Augsbourg (F 222), à droite, suivies du destroyer ouest-allemand Mölders (D 186), le destroyer britannique HMS Liverpool (D 92), le cuirassé de la marine américaine USS Iowa (BB-61) et le croiseur lance-missiles USS Ticonderoga (CG-47). Une force opérati...

Objects from antiquity, especially the civilizations of the Mediterranean For other uses, see Antiquities (disambiguation). A centaur struggling with a Lapith on a metope from the Parthenon, in the British Museum (London), part of the Elgin Marbles An Assyrian lamassu in the Louvre Chinese ritual wine server (guang), circa 1100 BC Antiquities are objects from antiquity, especially the civilizations of the Mediterranean: the Classical antiquity of Greece and Rome, Ancient Persia (Iran), Ancien...

Questa voce sull'argomento atleti giamaicani è solo un abbozzo. Contribuisci a migliorarla secondo le convenzioni di Wikipedia. Segui i suggerimenti del progetto di riferimento. Schillonie CalvertNazionalità Giamaica Altezza166 cm Peso57 kg Atletica leggera SpecialitàVelocità Società Racers Track Club Record 100 m 1105 (2011-2012) 200 m 2255 (2011) CarrieraNazionale 2012- Giamaica Palmarès Competizione Ori Argenti Bronzi Giochi olimpici 0 1 0 Mondiali 1 0 0 World Relays 1 1 0...

Online entertainment media company Tubefilter, Inc.Company typePrivateIndustryInternet, Media, EntertainmentFounded2008; 16 years ago (2008)[1]FounderDrew BaldwinBrady Brim-DeForestMarc Hustvedt[2]HeadquartersLos Angeles, California, United StatesKey peopleBrady Brim-DeForest (CEO)Websitewww.tubefilterinc.com Tubefilter, Inc. is a privately held company based in Los Angeles, California that operates media businesses focusing on the online entertainment indus...














![{\displaystyle \lambda _{\text{L}}={64 \over \operatorname {Re} }\left[1+{\operatorname {He} \over 6\operatorname {Re} }-{64 \over 3}\left({\operatorname {He} ^{4} \over \lambda _{\text{L}}^{3}\operatorname {Re} ^{7}}\right)\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/e8962b95c19253e478cd79cf2d2f7f5757df776e)










![{\displaystyle a=-1.47\left[1+0.146e^{-2.9\times {10^{-5}}\operatorname {He} }\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/dc7062b64baa347d8b2dbb4f949bec3947dface0)




![{\displaystyle f=\left[{f_{\text{L}}}^{m}+{f_{\text{T}}}^{m}\right]^{\frac {1}{m}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/c84af4c66e7a89fc1708426ea5b6b17bc23f31a3)
