Stokastik süreç
|
Read other articles:
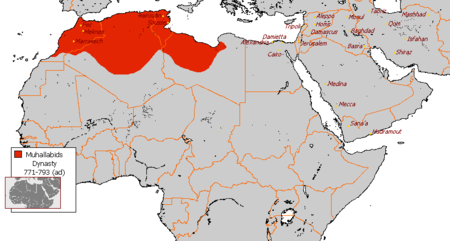
Artikel ini sebatang kara, artinya tidak ada artikel lain yang memiliki pranala balik ke halaman ini.Bantulah menambah pranala ke artikel ini dari artikel yang berhubungan atau coba peralatan pencari pranala.Tag ini diberikan pada Februari 2023. Dinasti MuhallabiyahالمهلبيونWilayah kekuasaan Dinasti Muhallabiyah pada tahun 771-793 MKeluarga indukAzd[1]NegaraKekhalifahan Umayyah dan Kekhalifahan Abbasiyah Ifriqiya Basra Ahwaz Khurasan Tempat asalDibba, Semenanjung Arab[2&#...

Ini adalah nama India; nama Patel merupakan patronimik, bukan nama keluarga, dan tokoh ini dipanggil menggunakan nama depannya, Karan. Karan PatelKaran Patel di Karpet Merah ITA Awards 2015Lahir23 November 1983 (umur 40)[1]Calcutta, West Bengal, IndiaPekerjaanAktorTahun aktif2005–sekarangSuami/istriAnkita Bhargava (2015–sekarang) Karan Patel (lahir 23 November 1983)[1] adalah seorang aktor berkebangsaan India. Berada di puncak popularitas berkat perannya sebagai ...

This article provides insufficient context for those unfamiliar with the subject. Please help improve the article by providing more context for the reader. (April 2013) (Learn how and when to remove this template message) BlackhawksThe New 52 Blackhawks, art by Ken Lashley.Publication informationPublisherDC ComicsFirst appearanceBlackhawks #1 (September 2011) Blackhawks was a monthly series launched by DC Comics in September 2011. The series had no direct ties to previous incarnations of DC's...

Universitas TwenteMotoHigh Tech, Human TouchJenisPublikDidirikan1961Dana abadi€304.5M[1]RektorTom VeldkampStaf administrasi2.602 (2016)Jumlah mahasiswa9.645 (2016)LokasiEnschede, BelandaSitus webwww.utwente.nl/en Menara Drienerlo di kampus. Universitas Twente (Bahasa Belanda: Universiteit Twente), sering disingkat sebagai UT, adalah sebuah universitas yang terletak di Enschede, Belanda. Universitas ini menawarkan program penelitian dan studi dalam bidang ilmu-ilmu sosial dan perilak...

Diego Castro Informasi pribadiNama lengkap Diego Castro GiménezTanggal lahir 2 Juli 1982 (umur 41)Tempat lahir Pontevedra, SpanyolTinggi 1,74 m (5 ft 9 in)Posisi bermain SayapInformasi klubKlub saat ini GetafeNomor 17Karier junior AJ LérezKarier senior*Tahun Tim Tampil (Gol)2001–2003 Pontevedra 63 (14)2003–2006 Málaga B 90 (2)2005–2006 Málaga 2 (0)2006–2011 Sporting Gijón 170 (39)2011– Getafe 31 (7) * Penampilan dan gol di klub senior hanya dihitung dari li...

Piala EFL 2017–20182017–18 EFL CupNegara Inggris WalesTanggal penyelenggaraan8 Agustus 2017 s.d. 25 Februari 2018Jumlah peserta92Juara bertahanManchester UnitedJuaraManchester City(gelar ke-5)Tempat keduaArsenalJumlah pertandingan87Jumlah gol258 (2.97 per pertandingan)Jumlah penonton1.454.812 (16.722 per pertandingan)Pencetak gol terbanyakJosh MurphySamuel SáizIslam Slimani(4 gol)← 2016–2017 2018–2019 → Piala EFL 2017–2018 adalah edisi ke-58 penyelenggaraan Piala...

Одногорбый верблюд Одногорбый верблюд в караване для транспортировки соли в Эфиопии Научная классификация Домен:ЭукариотыЦарство:ЖивотныеПодцарство:ЭуметазоиБез ранга:Двусторонне-симметричныеБез ранга:ВторичноротыеТип:ХордовыеПодтип:ПозвоночныеИнфратип:Челюстн...

Peta wilayah Kekaisaran Romawi c. 400 M. Praeses ( Latin pl. praesides ) dalam bahasa Latin berarti diletakkan sebelumnya atau di kepala. [1] Pada zaman Romawi Kuno di bawah dominasi Romawi, istilah ini digunakan untuk menyebutkan posisi gubernur Romawi; kata ini tetap digunakan untuk beberapa jabatan modern. Gubernur Romawi Praeses mulai digunakan untuk mendeskripsikan jabatan gubernur dalam sebuah provinsi Romawi —sering kali digunakan sebagai parafrase, seperti qui prae...

God Defend New ZealandB. Indonesia: Tuhan Lindungilah Selandia BaruTeks lagu God Defend New ZealandLagu kebangsaan Selandia BaruAliasAotearoa (versi bahasa Māori)Penulis lirikThomas Bracken, 1870-anKomponisJohn Joseph Woods, 1876Penggunaan1940 (sebagai himne nasional)1977 (sebagai lagu kebangsaan)Sampel audioInstrumen God Defend New Zealandberkasbantuan Sampel audioGod Defend New Zealandberkasbantuan God Defend New Zealand (bahasa Māori: Aotearoa, Indonesia: Tuhan Lindungilah Selan...

Method for determining winner of races For other uses, see Photo finish (disambiguation). A photo finish record of the first triple dead heat in harness racing: Patchover, Payne Hall and Penny Maid at Freehold Raceway (US), October 1953 A photo finish occurs in a sporting race when multiple competitors cross the finishing line at nearly the same time. As the naked eye may not be able to determine which of the competitors crossed the line first, a photo or video taken at the finish line may be...

Railway in England Coventry to Leamington LineA CrossCountry Voyager service on the line at Milverton.OverviewStatusOperationalOwnerNetwork RailLocaleWest Midlands (region)TerminiCoventryLeamington SpaServiceSystemNational RailOperator(s)CrossCountryWest Midlands TrainsRolling stockClass 220Class 221Class 172HistoryOpened1851TechnicalNumber of tracks1–2Track gauge4 ft 8+1⁄2 in (1,435 mm) standard gauge Route map (Click to expand) vteCoventry–Leamington line Legen...

Les Deux Magots The Deux Magots inside the café Les Deux Magots (pengucapan bahasa Prancis: [le dø maɡo]) merupakan café yang sangat terkenal[1] di area Saint-Germain-des-Prés di Paris, Prancis. Dulunya memiliki reputasi sebagai tempat pertemuan elit sastra dan intelektual kota. Sekarang menjadi tujuan wisata yang populer. Reputasi historisnya berasal dari perlindungan seniman Surrealis, intelektual seperti Simone de Beauvoir dan Jean-Paul Sartre, dan penulis muda, seperti E...

Disambiguazione – Se stai cercando il campionato europeo di calcio Europa 2020, vedi Campionato europeo di calcio 2020. Questa voce sull'argomento Unione europea è solo un abbozzo. Contribuisci a migliorarla secondo le convenzioni di Wikipedia. Segui i suggerimenti del progetto di riferimento. Bandiera dell'Unione europea Europa 2020 (Europe 2020) è una strategia decennale proposta dalla Commissione europea il 3 marzo 2010 per promuovere una crescita intelligente, sostenibile e incl...

Ця стаття потребує додаткових посилань на джерела для поліпшення її перевірності. Будь ласка, допоможіть удосконалити цю статтю, додавши посилання на надійні (авторитетні) джерела. Зверніться на сторінку обговорення за поясненнями та допоможіть виправити недоліки. Мат...

John GrassBiographieNaissance 1836Décès 10 mai 1918Fort YatesSépulture Saint Peters Catholic Church Cemetery (d)Nom de naissance Matȟó WatȟákpeFormation École industrielle indienne de CarlisleEnfant John Grass, Jr. (d)modifier - modifier le code - modifier Wikidata John Grass ou Charging Bear (en lakota : Matȟó Watȟákpe), né en 1836 et mort le 10 mai 1918, est un chef de la tribu des Sihasapas du peuple Lakota entre les années 1870 et 1890[1]. Il combat à la bataille de Li...

「アプリケーション」はこの項目へ転送されています。英語の意味については「wikt:応用」、「wikt:application」をご覧ください。 この記事には複数の問題があります。改善やノートページでの議論にご協力ください。 出典がまったく示されていないか不十分です。内容に関する文献や情報源が必要です。(2018年4月) 古い情報を更新する必要があります。(2021年3月)出...

محكمة التحكيم الرياضيةمعلومات عامةالبداية 1984 الاسم الأصل Court of Arbitration for Sport (بالإنجليزية) الاسم المختصر TAS (بالفرنسية) CAS (بالإنجليزية) المؤسس اللجنة الأولمبية الدولية البلد سويسرا الشكل القانوني جمعية تطوعية المقر الرئيسي لوزان على الخريطة المشغل International Council of Arbitration for Sport...

1982 studio album by AerosmithRock in a Hard PlaceStudio album by AerosmithReleasedAugust 27, 1982[1]Recorded1981–1982Studio Power Station, New York City Criteria, Miami GenreHard rockLength40:16LabelColumbiaProducer Jack Douglas Steven Tyler Tony Bongiovi Aerosmith chronology Night in the Ruts(1979) Rock in a Hard Place(1982) Done with Mirrors(1985) Rock in a Hard Place is the seventh studio album by American hard rock band Aerosmith, released on August 27, 1982, by Columb...

Pour les articles homonymes, voir Prudence. Cet article est une ébauche concernant la philosophie. Vous pouvez partager vos connaissances en l’améliorant (comment ?) selon les recommandations des projets correspondants. La Prudence, représentation du gisant de François II de Bretagne La Prudence. Statue de Frison pour l'Opéra de Paris (1875).Photo Durandelle La prudence (en grec φρόνησις [phronêsis] ; en latin prudentia[n 1]) est un concept de la philosophie grecque...

Diplomasi bilateral (antar dua negara) yang diwakili oleh Menlu RI Retno Marsudi dengan Sekretaris Luar Negeri Britania Raya Dominic Raab pada tahun 2021 di Gedung Pancasila Praktik diplomasi secara bilateral antara PM Kanada Justin Trudeau (kanan) dengan Ketua Kepala Staf Gabungan Amerika Serikat Joseph Dunford (kiri) pada tahun 2018 Dua diplomat sedang bernegosiasi Diplomasi (serapan dari Belanda: diplomatiecode: nl is deprecated ) adalah praktik mempengaruhi keputusan dan perilaku pemerint...














![{\displaystyle [f(x_{1}),\dots ,f(x_{n})]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/0039fe22d49daee6eb148604a65805718f5bfef3)










