Holografi ilkesi
|
Read other articles:

Questa voce o sezione sull'argomento fonetica non cita le fonti necessarie o quelle presenti sono insufficienti. Puoi migliorare questa voce aggiungendo citazioni da fonti attendibili secondo le linee guida sull'uso delle fonti. Fricativa labiodentale sonoraIPA - numero129 IPA - testov IPA - immagine UnicodeU+0076 Entityv SAMPAv X-SAMPAv Kirshenbaumv Ascoltonoicon La fricativa labiodentale sonora è una consonante molto frequente in numerose lingue, che in base all'alfabeto fon...

BlackbirdsPoster filmSutradaraJ. P. McGowanProduserJesse LaskyMorris GestDitulis olehHarry James Smith (sandiwara: Blackbirds)Margaret Turnbull (skenario)SinematograferCharles RosherDistributorParamount PicturesTanggal rilis 14 Oktober 1915 (1915-10-14) Durasi5 rolNegaraAmerika SerikatBahasaBisu (intertitel Inggris) Blackbirds adalah sebuah film drama bisu Amerika Serikat tahun 1915 yang diproduseri oleh Jesse Lasky dan didistribusikan melalui Paramount Pictures. Film tersebut menandai p...

Barony in the Peerage of the United Kingdom This article relies largely or entirely on a single source. Relevant discussion may be found on the talk page. Please help improve this article by introducing citations to additional sources.Find sources: Baron Brabazon of Tara – news · newspapers · books · scholar · JSTOR (April 2020) Baron Brabazon of Tara, of Sandwich in the County of Kent, is a title in the Peerage of the United Kingdom. It was created on...

ساينت كليرسفيل الإحداثيات 40°04′46″N 80°54′05″W / 40.0794°N 80.9014°W / 40.0794; -80.9014 [1] تاريخ التأسيس 1801 تقسيم إداري البلد الولايات المتحدة[2][3] التقسيم الأعلى مقاطعة بلمونت عاصمة لـ مقاطعة بلمونت خصائص جغرافية المساحة 6.310693 كيلومتر مرب�...

Football match1993 Football League Cup finalEvent1992–93 Football League Cup Arsenal Sheffield Wednesday 2 1 Date18 April 1993VenueWembley Stadium, LondonMan of the MatchPaul Merson (Arsenal)RefereeAllan GunnAttendance74,007← 1992 1994 → The 1993 Football League Cup final took place on 18 April 1993 at Wembley Stadium, and was played between Arsenal and Sheffield Wednesday. Arsenal won 2–1 in normal time, in what was the first of three Wembley finals between the two sides tha...

Cuyo Rugby UnionUnión de Rugby de CuyoSportRugby unionJurisdictionMendoza ProvinceAbbreviationURCFoundedSeptember 22, 1945; 78 years ago (1945-09-22)AffiliationUARHeadquartersGodoy Cruz, MendozaPresidentJavier Pellegrina (2023)[1]Vice president(s)Federico CoriaSecretaryMartín FlamariqueOfficial websitewww.unionderugbydecuyo.com.ar The Cuyo Rugby Union (Spanish: Unión de Rugby de Cuyo) (also known for its initials URC) is the organisational body that rules the game...

State of being responsible for a crime per the state's rules Guilty party redirects here. For other uses, see Guilty Party (disambiguation). This article needs additional citations for verification. Please help improve this article by adding citations to reliable sources. Unsourced material may be challenged and removed.Find sources: Guilt law – news · newspapers · books · scholar · JSTOR (June 2007) (Learn how and when to remove this message) Cri...

AinuRumah Ainu Karafuto, 1912Jumlah populasi300 (Sensus Rusia 2021)[1] 1.000 hingga +100.000[butuh rujukan] (tidak diakui di tingkat federal)Daerah dengan populasi signifikanOblast Sakhalin, Krai Khabarovsk dan Krai KamchatkaBahasaRusia, sebelumnya bahasa-bahasa Ainu (Kuril†, Sakhalin†)AgamaOrtodoks Rusia dan Syamanisme (lihat mitologi Ainu)Kelompok etnik terkaitAinu Hokkaido, Kamchadal, Ryukyu,[2] Jōmon Suku Ainu Kuril di dalam tempat tinggal tradisional mereka, ...

Schematic of the active CUSP system for 70-Tfps imaging Femto-photography is a technique for recording the propagation of ultrashort pulses of light through a scene at a very high speed (up to 1013 frames per second). A femto-photograph is equivalent to an optical impulse response of a scene and has also been denoted by terms such as a light-in-flight recording[1] or transient image.[2][3] Femto-photography of macroscopic objects was first demonstrated using a holograp...

Questa voce sull'argomento centri abitati del Michigan è solo un abbozzo. Contribuisci a migliorarla secondo le convenzioni di Wikipedia. Segui i suggerimenti del progetto di riferimento. East LansingcityEast Lansing – Veduta LocalizzazioneStato Stati Uniti Stato federato Michigan ConteaInghamClinton AmministrazioneSindacoVictor W. Loomis, Jr. TerritorioCoordinate42°44′05.28″N 84°28′50.88″W / 42.7348°N 84.4808°W42.7348; -84.4808 (East Lansing)C...

烏克蘭總理Прем'єр-міністр України烏克蘭國徽現任杰尼斯·什米加尔自2020年3月4日任命者烏克蘭總統任期總統任命首任維托爾德·福金设立1991年11月后继职位無网站www.kmu.gov.ua/control/en/(英文) 乌克兰 乌克兰政府与政治系列条目 宪法 政府 总统 弗拉基米尔·泽连斯基 總統辦公室 国家安全与国防事务委员会 总统代表(英语:Representatives of the President of Ukraine) 总...

烏克蘭總理Прем'єр-міністр України烏克蘭國徽現任杰尼斯·什米加尔自2020年3月4日任命者烏克蘭總統任期總統任命首任維托爾德·福金设立1991年11月后继职位無网站www.kmu.gov.ua/control/en/(英文) 乌克兰 乌克兰政府与政治系列条目 宪法 政府 总统 弗拉基米尔·泽连斯基 總統辦公室 国家安全与国防事务委员会 总统代表(英语:Representatives of the President of Ukraine) 总...

City gate in Marrakesh, Morocco Bab Aghmatباب أغماتBab Aghmat in the early 20th centuryGeneral informationTypecity gateArchitectural styleAlmoravid, Moorish, MoroccanLocationMarrakesh, MoroccoCoordinates31°37′25.2″N 7°58′29.4″W / 31.623667°N 7.974833°W / 31.623667; -7.974833Completedcirca 1126 Bab Aghmat (Arabic: باب أغمات, lit. 'gate of Aghmat') is the main southeastern gate of the medina (historic walled city) of Marrakesh, M...

Shinano Railway Kita-Shinano LineA Shinano Railway SR1 series EMU, between Furuma and KurohimeOverviewNative nameしなの鉄道北しなの線OwnerShinano RailwayLocaleNagano PrefectureTerminiNaganoMyōkō-KōgenStations8ServiceTypeCommuter railRolling stock115 series EMUsHistoryOpened1 May 188814 March 2015 (2015-03-14) (As the private railway line)TechnicalLine length37.3 km (23.2 mi)Track gauge1,067 mm (3 ft 6 in)Electrification1,500 V DC Rout...
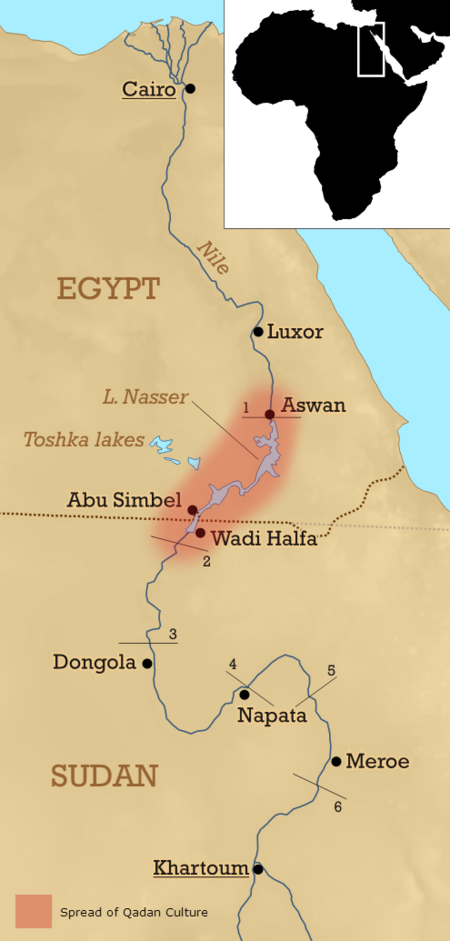
ثقافة قادانمصر العليا - يظهر انتشار ثقافة قادان على طول نهر النيل (منذ حوالي 15000 سنة)المعطياتالنطاق الجغرافيمصر العلياالفترةالعصر الحجري المتوسطتواريخ15,000 BP — 11,000 BPأهم المواقعالمقبرة 117يسبقهاسيبيليةيليهاهريفيان كانت ثقافة قادان (13000-9000 قبل الميلاد) عبارة عن ثقافة قديمة ت�...

مانويل الثاني باليولوج إمبراطور الامبراطورية البيزنطية الإمبراطور مانويل الثاني فترة الحكم 1391 – 1425 يوحنا الخامس باليولوج يوحنا الثامن باليولوج معلومات شخصية الميلاد 27 يوليو 1350القسطنطينية الوفاة 21 يوليو 1425 (75 سنة) القسطنطينية مواطنة الإمبراطورية البيزنطية ...

This article needs additional citations for verification. Please help improve this article by adding citations to reliable sources. Unsourced material may be challenged and removed.Find sources: Tofutti – news · newspapers · books · scholar · JSTOR (July 2017) (Learn how and when to remove this message) Tofutti Brands, Inc.Company typePublicTraded asOTCQX: TOFBIndustrySoy products manufacturerFounded1981FounderDavid MintzHeadquartersCranford, New ...

12th-century conflict Battle of HabPart of the CrusadesMap of the battle of Hab in 1119 (from 1898)DateAugust 14, 1119LocationBurj Hab, near Ariha, (modern Syria)Result Crusader victory[1]Belligerents Kingdom of JerusalemCounty of TripoliPrincipality of Antioch Artuqids of AleppoCommanders and leaders Baldwin II of JerusalemPons of TripoliRobert Fulcoy. (esir edilip öldürüldü) Ilghazi of MardinStrength 700 cavalry with several thousand infantry[2] UnknownCasualties a...

Bagian dari seriGereja Katolik menurut negara Afrika Afrika Selatan Afrika Tengah Aljazair Angola Benin Botswana Burkina Faso Burundi Chad Eritrea Eswatini Etiopia Gabon Gambia Ghana Guinea Guinea-Bissau Guinea Khatulistiwa Jibuti Kamerun Kenya Komoro Lesotho Liberia Libya Madagaskar Malawi Mali Maroko Mauritania Mauritius Mesir Mozambik Namibia Niger Nigeria Pantai Gading Republik Demokratik Kongo Republik Kongo Rwanda Sao Tome dan Principe Senegal Seychelles Sierra Leone Somalia Somaliland ...

Argentine folk music genre This article has multiple issues. Please help improve it or discuss these issues on the talk page. (Learn how and when to remove these template messages) You can help expand this article with text translated from the corresponding article in Spanish. (October 2021) Click [show] for important translation instructions. View a machine-translated version of the Spanish article. Machine translation, like DeepL or Google Translate, is a useful starting point for tran...
