Lipschitzkontinuitet
|
Read other articles:

مرحبا بكم في رايليزWelcome to the Rileys (بالإنجليزية) معلومات عامةالصنف الفني فيلم دراما[1][2][3] المواضيع دعارة — عائلة مختلة تاريخ الصدور 2010 7 أبريل 2011[4] (ألمانيا) مدة العرض 110 دقيقة اللغة الأصلية الإنجليزية البلد الولايات المتحدة المملكة المتحدة موقع التصوير ...
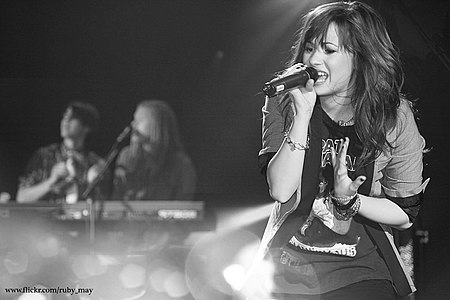
Penampilan Demi Lovato pada saat konser tahun 2008 Penyanyi asal Amerika Serikat, Demi Lovato telah merekam enam album studio. Sebelum memulai karier musiknya, Lovato membintangi film televisi musikal Disney Channel, Camp Rock.[1] Duet Lovato dengan Joe Jonas, This Is Me, dirilis sebagai single dari soundtrack film, memuncak di nomor sembilan di Billboard Hot 100 dan berada di posisi dua puluh teratas di beberapa tangga lagu internasional. Setelah menandatangani kontrak dengan Hollywo...

Public sculpture by George Grey Barnard Statue of Abraham LincolnStatue of Lincoln at Lytle Park. The Taft Museum of Art stands in the background.Statue of Abraham LincolnArtistGeorge Grey BarnardYear1917 (1917)MediumBronzeSubjectAbraham LincolnDimensions3.4 m (11 ft)LocationLytle Park, CincinnatiCoordinates39°06′04″N 84°30′15″W / 39.101168°N 84.504299°W / 39.101168; -84.504299 An 11-foot (3.4 m) bronze statue of Abraham Lincoln is i...

Jungwoo Kim Jungwoo (김정우, lahir 19 Februari 1998) adalah seorang penyanyi Korea Selatan di bawah kontrak SM Entertainment. Ia adalah anggota grup vokal laki-laki NCT dan sub-unit NCT U dan NCT 127.[1] Referensi ^ New NCT unit to debut this July! | allkpop.com. allkpop. Diakses tanggal 2017-07-17.

This article needs additional citations for verification. Please help improve this article by adding citations to reliable sources. Unsourced material may be challenged and removed.Find sources: PowerBook 500 series – news · newspapers · books · scholar · JSTOR (April 2023) (Learn how and when to remove this template message) Range of Apple Macintosh PowerBook portable computers PowerBook 500 seriesThe PowerBook 540cDeveloperApple ComputerManufacturerA...

Justice LeaguePoster rilis teatrikalSutradaraZack SnyderProduserCharles Roven, Deborah Snyder, Jon Berg, Geoff JohnsSkenarioChris Terrio, Joss WhedonCerita Chris Terrio Zack Snyder BerdasarkanJustice Leagueoleh Gardner FoxPemeran Ben Affleck Henry Cavill Gal Gadot Ezra Miller Jason Momoa Ray Fisher Amy Adams Jeremy Irons Diane Lane Connie Nielsen J. K. Simmons Ciarán Hinds Penata musikDanny ElfmanSinematograferFabian WagnerPenyunting David Brenner Richard Pearson Martin Walsh Perusahaa...

Rutpela Rutpela maculata Klasifikasi ilmiah Kerajaan: Animalia Filum: Arthropoda Kelas: Insecta Ordo: Coleoptera Famili: Cerambycidae Subfamili: Lepturinae Tribus: Lepturini Genus: Rutpela Rutpela adalah genus kumbang tanduk panjang yang tergolong famili Cerambycidae. Genus ini juga merupakan bagian dari ordo Coleoptera, kelas Insecta, filum Arthropoda, dan kingdom Animalia. Larva kumbang dalam genus ini biasanya mengebor ke dalam kayu dan dapat menyebabkan kerusakan pada batang kayu hidup a...

Mathematical model of interest rates A trajectory of the short rate and the corresponding yield curves at T=0 (purple) and two later points in time In finance, the Vasicek model is a mathematical model describing the evolution of interest rates. It is a type of one-factor short-rate model as it describes interest rate movements as driven by only one source of market risk. The model can be used in the valuation of interest rate derivatives, and has also been adapted for credit markets. It was ...

Species of flowering plant Prairie onion Conservation status Secure (NatureServe)[1] Scientific classification Kingdom: Plantae Clade: Tracheophytes Clade: Angiosperms Clade: Monocots Order: Asparagales Family: Amaryllidaceae Subfamily: Allioideae Genus: Allium Subgenus: A. subg. Amerallium Species: A. textile Binomial name Allium textileA.Nelson & J.F.Macbr.[2] Synonyms[3][4] Synonymy Allium angulosum Pursh 1813, illegitimate homonym not L. 1753...

莎拉·阿什頓-西里洛2023年8月,阿什頓-西里洛穿著軍服出生 (1977-07-09) 1977年7月9日(46歲) 美國佛羅里達州国籍 美國别名莎拉·阿什頓(Sarah Ashton)莎拉·西里洛(Sarah Cirillo)金髮女郎(Blonde)职业記者、活動家、政治活動家和候選人、軍醫活跃时期2020年—雇主內華達州共和黨候選人(2020年)《Political.tips》(2020年—)《LGBTQ國度》(2022年3月—2022年10月)烏克蘭媒�...

Le decisioni di Pisino o decisioni di settembre (in croato Pazinske odluke o Rujanske odluke) sono decisioni manifeste del Comitato nazionale di liberazione per l'Istria adottate a Pisino il 13 settembre 1943 e dal Parlamento dei rappresentanti del popolo istriano del 26 settembre 1943 per proclamare unilateralmente l'annessione dell'Istria alla Repubblica Socialista di Croazia e alla Jugoslavia. All'epoca la penisola istriana era divisa tra provincia di Pola e provincia di Fiume ed era stata...

2016 U.S. presidential election Timeline General election debates Parties Polling national statewide by demographics international Newspaper endorsements primary general Russian interference Russia investigation origins counter-narrative Media coverage Social media International reactions Electors Recounts Faithless electors Vote count Republican Party Primaries Candidates Debates and forums Polling national statewide straw polls Endorsements Results Nominee VP candidate selection Convention...

Torneo de Fútbol femenino en los Juegos Panamericanos Toronto 2015 V Torneo de fútbol femenino Estadio de Fútbol Panamericano Hamilton CIBC, sede del torneo.Datos generalesSede CanadáCiudad HamiltonRecinto Estadio de Fútbol Panamericano Hamilton CIBCAsociación Conmebol y ConcacafFecha 11 de julio de 201525 de julio de 2015Edición 5PalmarésDef. título CAN Canadá01 ! Oro BRA Brasil02 ! Plata COL Colombia03 ! Bronce MEX MéxicoDatos estadísticosPartici...

يفتقر محتوى هذه المقالة إلى الاستشهاد بمصادر. فضلاً، ساهم في تطوير هذه المقالة من خلال إضافة مصادر موثوق بها. أي معلومات غير موثقة يمكن التشكيك بها وإزالتها. (يوليو 2017) العلاقات الـسعودية الهولندية السعودية هولندا السفارات سفارة خـادم الـحرمين الـشريفين في ام...

Cet article est une ébauche concernant la science-fiction. Vous pouvez partager vos connaissances en l’améliorant (comment ?) selon les recommandations des projets correspondants. Space Western Comics, bande dessinée mélangeant western et science fiction (1952). Le space western est un sous-genre de la science-fiction qui combine des éléments issus du western à ceux caractérisant le genre SF. Cela peut aller d'une simple influence du western sur le genre en question, comme la ...

Expo 1932Esposizione propagandisticaLogo Stato Italia CittàRoma TemaDecennale dell'avvento al potere di Benito Mussolini Periododal 28 ottobre 1932al 28 ottobre 1934 Visitatori3,855 milioni Cronologia Successiva 19371942 Manuale Cambio della guardia della MVSN davanti al palazzo della mostra Picchetto di Camicie Nere davanti al palazzo La Mostra della Rivoluzione fascista fu un evento celebrativo del decennale dell'avvento al potere di Benito Mussolini che si tenne per due anni e...

Плотность населения в Миннесоте Население штата Миннесота по переписи 2020 года составляет 5 706 494 человека[1]. Примерно 60% населения штата проживает в агломерации Миннеаполиса и Сент-Пола. Центр населённости Миннесоты расположен в округе Хеннепин, в городе Роджерс[2 ...

Direct 8Diluncurkan24 Juli 2001 (transmisi percobaan)31 Maret 2005 (peluncuran resmi)PemilikBolloréPangsa pemirsa1.0% (TNT) (Juni 2007, [1])Negara PrancisSitus webdirect8.fr Direct 8 merupakan sebuah jaringan televisi Prancis baru, dimiliki oleh Vincent Bolloré. Tersedia melalui jaringan televisi terrestrial digital TNT dan posisi satelit Hot Bird. Seperti namanya ('direct' adalah bahasa Prancis untuk 'langsung'), ditujukan untuk menyiarkan acara langsung saja (kecuali selama malam har...

بيرسيوس المقدوني (بالإغريقية: Περσεύς) معلومات شخصية الميلاد سنة 212 ق م بيلا الوفاة سنة 166 ق م الأب فيليب الخامس ملك مقدونيا عائلة الأسرة الأنتيغونية الحياة العملية المهنة عسكري اللغات الإغريقية تعديل مصدري - تعديل آخر ملوك مملكة مقدوني�...

Modern form of farming This article needs additional citations for verification. Please help improve this article by adding citations to reliable sources. Unsourced material may be challenged and removed.Find sources: Intensive crop farming – news · newspapers · books · scholar · JSTOR (March 2009) (Learn how and when to remove this message) Agriculture History Prehistory Neolithic Revolution Agriculture in Mesoamerica Austronesian expansion Ancient hi...
















































