–ü–ĺ–≤–Ķ–∑–į–Ĺ–į —Ā—ā—Ä—É–ļ—ā—É—Ä–į –Ņ–ĺ–ī–į—ā–į–ļ–į
|
Read other articles:

Yussuf Poulsen Informasi pribadiNama lengkap Yussuf Yurary Poulsen[1]Tanggal lahir 15 Juni 1994 (umur 29)Tempat lahir Kopenhagen, DenmarkTinggi 192 cm (6 ft 4 in)[2]Posisi bermain PenyerangInformasi klubKlub saat ini RB LeipzigNomor 9Karier junior BK Skjold0000‚Äď2011 Lyngby BKKarier senior*Tahun Tim Tampil (Gol)2011‚Äď2013 Lyngby BK 35 (11)2013‚Äď RB Leipzig 242 (63)Tim nasional‚Ä°2010 Denmark U-16 1 (0)2010‚Äď2011 Denmark U-17 19 (2)2011‚Äď2012 Denmark U...

Pemilihan umum Presiden Amerika Serikat 1940193619445 November 1940531 suara elektoral lembaga pemilihan266 suara elektoral untuk menang untuk menangKandidat Calon Franklin D. Roosevelt Wendell Willkie Partai Demokrat Republik Negara bagian New York[1] New York[1] Pendamping Henry A. Wallace Charles L. McNary Suara elektoral 449 82 Negara bagian 38 10 Suara rakyat 27.313.945 22.347.744 Persentase 54,7% 44,8% Peta persebaran suara Hasil pemilihan pre...

Piala FA 2015‚Äď2016Football Association Challenge CupNegara Inggris Guernsey WalesTanggal penyelenggaraan15 Agustus 2015 ‚Äď 21 Mei 2016Jumlah peserta736JuaraManchester UnitedTempat keduaCrystal Palace‚Üź 2014‚Äď2015 2016‚Äď2017 ‚Üí Piala FA 2015‚Äď2016 (juga dikenal dengan nama Piala Challenge FA) merupakan edisi ke 135 dalam penyelenggaran Piala FA. Pada musim ini, Emirates menjadi sponsor resmi turnamen, sehingga juga disebut dengan Emirates FA Cup.[1] Kompetisi dimulai denga...

Der Titel dieses Artikels ist mehrdeutig. Weitere Bedeutungen sind unter Der Kaufmann von Venedig (Begriffskl√§rung) aufgef√ľhrt. Der Kaufmann von Venedig (englisch The Merchant of Venice) ist ein Theaterst√ľck von William Shakespeare. Das Werk entstand zwischen 1596 und 1598 und wurde 1600 in der ersten Quartoausgabe ver√∂ffentlicht. Die fr√ľheste bekannte Auff√ľhrung fand am 10. Februar 1605 vor K√∂nig Jakob I. im Palace of Whitehall statt. Das St√ľck spielt in Venedig und in Belmont, eine...
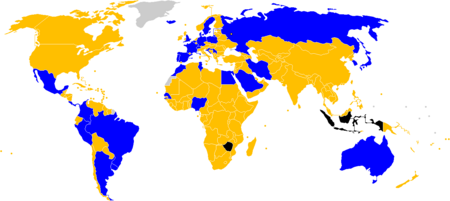
Kualifikasi Piala Dunia FIFA 2018Informasi turnamenJadwalpenyelenggaraan12 Maret 2015 sampai 14 November 2017Jumlahtim peserta210 (dari 6 konfederasi)← 2014 2022 → Kualifikasi Piala Dunia FIFA 2018 akan menentukan 31 dari 32 tim nasional sepak bola yang akan berlaga di putaran final Piala Dunia FIFA 2018, di mana tuan rumah Rusia akan otomastis terkualifikasi. Semua 210 anggota FIFA akan mengikuti kualifikasi ini. Untuk pertama kalinya dalam sejarah piala dunia, semua tim nas...

–ó–į–Ņ—Ä–ĺ—Ā ¬ę–ü—É–≥–į—á—Ď–≤–į¬Ľ –Ņ–Ķ—Ä–Ķ–Ĺ–į–Ņ—Ä–į–≤–Ľ—Ź–Ķ—ā—Ā—Ź —Ā—é–ī–į; —Ā–ľ. —ā–į–ļ–∂–Ķ –ī—Ä—É–≥–ł–Ķ –∑–Ĺ–į—á–Ķ–Ĺ–ł—Ź. –ź–Ľ–Ľ–į –ü—É–≥–į—á—Ď–≤–į –Ě–į —Ą–Ķ—Ā—ā–ł–≤–į–Ľ–Ķ ¬ę–°–Ľ–į–≤—Ź–Ĺ—Ā–ļ–ł–Ļ –Ī–į–∑–į—Ä –≤ –í–ł—ā–Ķ–Ī—Ā–ļ–Ķ¬Ľ, 2016 –≥–ĺ–ī –ě—Ā–Ĺ–ĺ–≤–Ĺ–į—Ź –ł–Ĺ—Ą–ĺ—Ä–ľ–į—Ü–ł—Ź –ü–ĺ–Ľ–Ĺ–ĺ–Ķ –ł–ľ—Ź –ź–Ľ–Ľ–į –Ď–ĺ—Ä–ł—Ā–ĺ–≤–Ĺ–į –ü—É–≥–į—á—Ď–≤–į –Ē–į—ā–į —Ä–ĺ–∂–ī–Ķ–Ĺ–ł—Ź 15 –į–Ņ—Ä–Ķ–Ľ—Ź 1949(1949-04-15) (75 –Ľ–Ķ—ā) –ú–Ķ—Ā—ā–ĺ —Ä–ĺ–∂–ī–Ķ–Ĺ–ł—Ź –ú–ĺ—Ā–ļ–≤–į, –°–°–°–†[1]...

49th season of FIA Formula One motor racing F1 1995 redirects here. For the video games based on the 1995 Formula One season, see Formula 1 (video game). 1995 FIA Formula OneWorld Championship Drivers' Champion: Michael SchumacherConstructors' Champion: Benetton-Renault Previous 1994 Next 1996 Races by countryRaces by venueSupport series: Porsche Supercup Defending world champion Michael Schumacher (pictured in 2005) won a second consecutive title with Benetton in his last year with the team....

–Ě–ĺ–≤–ĺ–≥—Ä—É–ī—Ā–ļ–į—Ź –Ķ–Ņ–į—Ä—Ö–ł—Ź –°–≤—Ź—ā–ĺ-–Ě–ł–ļ–ĺ–Ľ—Ć—Ā–ļ–ł–Ļ –ļ–į—Ą–Ķ–ī—Ä–į–Ľ—Ć–Ĺ—č–Ļ —Ā–ĺ–Ī–ĺ—Ä –≤ –≥. –Ě–ĺ–≤–ĺ–≥—Ä—É–ī–ļ–Ķ –°—ā—Ä–į–Ĺ–į –Ď–Ķ–Ľ–ĺ—Ä—É—Ā—Ā–ł—Ź –¶–Ķ—Ä–ļ–ĺ–≤—Ć –Ď–Ķ–Ľ–ĺ—Ä—É—Ā—Ā–ļ–ł–Ļ —ć–ļ–∑–į—Ä—Ö–į—ā –†–ü–¶ –Ē–į—ā–į –ĺ—Ā–Ĺ–ĺ–≤–į–Ĺ–ł—Ź 1415 –£–Ņ—Ä–į–≤–Ľ–Ķ–Ĺ–ł–Ķ –ď–Ľ–į–≤–Ĺ—č–Ļ –≥–ĺ—Ä–ĺ–ī –Ě–ĺ–≤–ĺ–≥—Ä—É–ī–ĺ–ļ –ö–į—Ą–Ķ–ī—Ä–į–Ľ—Ć–Ĺ—č–Ļ —Ā–ĺ–Ī–ĺ—Ä –°–≤—Ź—ā–ĺ-–Ě–ł–ļ–ĺ–Ľ—Ć—Ā–ļ–ł–Ļ (–Ě–ĺ–≤–ĺ–≥—Ä—É–ī–ĺ–ļ) –ė–Ķ—Ä–į—Ä—Ö –ź—Ä—Ö–ł–Ķ–Ņ–ł—Ā–ļ–ĺ–Ņ –Ě–ĺ–≤–ĺ–≥—Ä—É–ī—Ā–ļ–ł–Ļ –ł –°ÔŅĹ...

Major League Baseball team season 1877 Cincinnati RedsLeagueNational LeagueBallparkAvenue GroundsCityCincinnatiManagersLip Pike, Bob Addy, Jack Manning ← 1876 Seasons 1878 → The 1877 Cincinnati Reds season was the team's second season in the National League. The team finished sixth and last in the league with a record of 15‚Äď42, 25¬Ĺ games behind the first place Boston Red Caps.[1] Regular season Lip Pike After finishing dead last in the National League in...

ś≠§śĚ°ÁõģŚļŹŤ®ÄÁꆍäāś≤°śúČŚÖÖŚąÜśÄĽÁĽďŚÖ®śĖáŚÜÖŚģĻŤ¶ĀÁāĻ„Äā (2019ŚĻī3śúą21śó•)ŤĮ∑ŤÄÉŤôϜȩŚÖÖŚļŹŤ®ÄԾƜłÖśôįś¶āŤŅįśĚ°ÁõģśČÄśúČťá杼ě„ÄāŤĮ∑Śú®śĚ°ÁõģÁöĄŤģ®Ťģļť°ĶŤģ®Ťģļś≠§ťóģťĘė„Äā ŚďąŤź®ŚÖčśĖĮŚĚ¶ÁłĹÁĶĪŚďąŤĖ©ŚÖčÁłĹÁĶĪśóóÁŹĺšĽĽ“ö–į—Ā—č–ľ-–Ė–ĺ–ľ–į—Ä—ā –ö–Ķ–ľ–Ķ–Ľ“Ī–Ľ—č –Ę–ĺ“õ–į–Ķ–≤Ść°ÁĎüŚßÜŤč•ť©¨ŚįĒÁČĻ¬∑śČėŚć°ŤÄ∂Ś§ęŤá™2019ŚĻī3śúą20śó•Śú®šĽĽšĽĽśúü7ŚĻīť¶ĖšĽĽŚä™ŚįĒŤčŹšłĻ¬∑Áļ≥śČéŚįĒŚ∑īŤÄ∂Ś§ęŤģĺÁęč1990ŚĻī4śúą24śó•ÔľąŚďąŤĖ©ŚÖčŤėáÁ∂≠ŚüÉÁ§ĺśúÉšłĽÁĺ©ŚÖĪŚíĆŚúčÁłĹÁĶĪÔľČ ŚďąŤź®ŚÖčśĖĮŚĚ¶ ŚďąŤź®ŚÖčśĖĮŚĚ¶śĒŅŚļú...

Pour l‚Äôarticle homonyme, voir Gougark. Gugark (hy) ‘≥’ł÷ā’£’°÷Ä÷Ą L'entr√©e de Gugark Administration Pays Arm√©nie R√©gion Lorri Maire Mandat Ashot Ashughyan (HHK)[1],[2] 2012-2016 D√©mographie Population 6 562 hab. (2008) Densit√© 304 hab./km2 G√©ographie Coordonn√©es 40¬į 48‚Ä≤ 26‚Ä≥ nord, 44¬į 32‚Ä≤ 17‚Ä≥ est Superficie 2 158 ha = 21,58 km2 Fuseau horaire UTC+4 Localisation G√©olocalisation sur la carte : Arm√©ni...

Race car class This article is about the third tier of single-seater racing. For the current international championship of the same name, see FIA Formula 3 Championship. This article needs additional citations for verification. Please help improve this article by adding citations to reliable sources. Unsourced material may be challenged and removed.Find sources: Formula Three ‚Äď news ¬∑ newspapers ¬∑ books ¬∑ scholar ¬∑ JSTOR (April 2022) (Learn how and whe...

ō•Ŕäōįōßō° ōßŔĄŔÜŔĀō≥ ō¨ōĪŔąō≠ ŔĀŔä ōßŔĄŔäōĮ ō®ō≥ō®ō® ō•Ŕäōįōßō° ōßŔĄŔÜŔĀō≥ ō®ōĘŔĄō© ō¨ōßōĪō≠ō©ō¨ōĪŔąō≠ ŔĀŔä ōßŔĄŔäōĮ ō®ō≥ō®ō® ō•Ŕäōįōßō° ōßŔĄŔÜŔĀō≥ ō®ōĘŔĄō© ō¨ōßōĪō≠ō© ŔÖōĻŔĄŔąŔÖōßō™ ōĻōßŔÖō© ōßŔĄōßōģō™ōĶōßōĶ ō∑ō® ŔÜŔĀō≥ŔäōĆ ŔąōĻŔĄŔÖ ōßŔĄŔÜŔĀō≥ ōßŔĄō≥ōĪŔäōĪŔä ŔÖŔÜ ō£ŔÜŔąōßōĻ ō•ōĶōßō®ō©ōĆ ŔąōßŔĄō™ōĻōĮŔä ōĻŔĄŔČ ōßŔĄŔÜŔĀō≥ōĆ ŔąŔÜōīōßō∑ ō•ŔÜō≥ōßŔÜŔä [ŔĄōļōßō™ ō£ōģōĪŔČ] ō™ōĻōĮŔäŔĄ ŔÖōĶōĮōĪŔä - ō™ōĻōĮŔäŔĄ ō•Ŕäōįōßō° ōßŔĄŔÜŔĀō≥ ō£Ŕą ō¨ōĪō≠ ōßÔŅĹ...

John Braithwaite Informaci√≥n personalNacimiento 19 de marzo de 1797 Londres (Reino de Gran Breta√Īa) Fallecimiento 25 de septiembre de 1870 (73 a√Īos)Londres (Reino Unido de Gran Breta√Īa e Irlanda) Sepultura Cementerio de Kensal Green Nacionalidad Brit√°nicaFamiliaPadre John Braithwaite the elder Informaci√≥n profesionalOcupaci√≥n Ingeniero civil, ingeniero e ingeniero ferroviario Distinciones Fellow of the Society of Antiquaries [editar datos en Wikidata] John Braithwaite, el jov...

–£ –í—Ė–ļ—Ė–Ņ–Ķ–ī—Ė—ó —Ē —Ā—ā–į—ā—ā—Ė –Ņ—Ä–ĺ —Ė–Ĺ—ą—Ė –∑–Ĺ–į—á–Ķ–Ĺ–Ĺ—Ź —Ü—Ć–ĺ–≥–ĺ —ā–Ķ—Ä–ľ—Ė–Ĺ–į: –ú–ö–°. –ú—Ė–∂–Ĺ–į—Ä–ĺ–ī–Ĺ–į –ļ–ĺ—Ā–ľ—Ė—á–Ĺ–į —Ā—ā–į–Ĺ—Ü—Ė—Ź –Ķ–ļ—Ė–Ņ–į–∂ 6 (–Ĺ–į –ļ–≤—Ė—ā–Ķ–Ĺ—Ć 2018 –Ĺ–į —Ā—ā–į–Ĺ—Ü—Ė—ó –Ņ–Ķ—Ä–Ķ–Ī—É–≤–į–Ľ–į 55 –Ķ–ļ—Ā–Ņ–Ķ–ī–ł—Ü—Ė—Ź)–ī–į—ā–į –∑–į–Ņ—É—Ā–ļ—É 20 –Ľ–ł—Ā—ā–ĺ–Ņ–į–ī–į 1998–ļ–ĺ—Ā–ľ–ĺ–ī—Ä–ĺ–ľ –Ď–į–Ļ–ļ–ĺ–Ĺ—É—Ä, –ľ–į–Ļ–ī–į–Ĺ—á–ł–ļ–ł –ď–į–≥–į—Ä—Ė–Ĺ—Ā—Ć–ļ–ł–Ļ —Ā—ā–į—Ä—ā —ā–į 81/23; –ö–¶ —Ė–ľ. –ö–Ķ–Ĺ–Ĺ–Ķ–ī—Ė, LC-39—Ā—ā–į—ā—É—Ā –ī—Ė—é—á–į–ľ–į—Ā–į ‚Čą 419...

Disambiguazione ‚Äď Se stai cercando altri significati, vedi Clock (disambigua). Questa voce o sezione sugli argomenti elettronica e hardware non cita le fonti necessarie o quelle presenti sono insufficienti. Puoi migliorare questa voce aggiungendo citazioni da fonti attendibili secondo le linee guida sull'uso delle fonti. Segui i suggerimenti del progetto di riferimento. Rappresentazione di un segnale di clock e della frequenza di clock Il termine clock, in elettronica, indica un segna...

Orville avec le planeur de 1901, le nez en haut Wilbur juste apr√®s l'atterrissage Le planeur Wright de 1901 √©tait le second planeur des Fr√®res Wright. Ils proc√©d√®rent aux essais √† Kill Devil Hills, √† six kilom√®tres au sud de Kitty Hawk. Configuration Ce planeur √©tait d√©riv√© du planeur biplan de l'ann√©e pr√©c√©dente, mais avec une envergure plus grande (22 pieds au lieu de 18). Il fut essay√© en vol du 27 juillet au 17 ao√Ľt 1901, effectuant entre 50 et 100 vols libres en suppl√©me...

śó•śú¨ > śĚĪšļ¨ťÉĹ > ŚćÉšĽ£ÁĒįŚĆļ > ÁīÄŚįĺšļēÁĒļ ÁīÄŚįĺšļēÁĒļ ÁīÄŚįĺšļēÁĒļÁīÄŚįĺšļēÁĒļ„ĀģšĹćÁĹģ ŚĆóÁ∑Į35Śļ¶40ŚąÜ53.68Áßí śĚĪÁĶĆ139Śļ¶44ŚąÜ2.02Áßí / ŚĆóÁ∑Į35.6815778Śļ¶ śĚĪÁĶĆ139.7338944Śļ¶ / 35.6815778; 139.7338944ŚõĹ śó•śú¨ťÉĹťĀďŚļúÁúĆ śĚĪšļ¨ÁČĻŚą•ŚĆļ ŚćÉšĽ£ÁĒįŚĆļŚúįŚüü ťļĻÁĒļŚúįŚüüšļļŚŹ£Ôľą2017ŚĻīÔľąŚĻ≥śąź29ŚĻīÔľČ12śúą1śó•ÁŹĺŚú®ÔľČ[1] ‚ÄĘ ŚźąŤ®ą 452šļļÁ≠ČśôāŚłĮ UTC+9 (śó•śú¨ś®ôśļĖśôā)ťÉĶšĺŅÁē™ŚŹ∑ 102-0094[2]ŚłāÔŅĹ...

Body of sovereignty of the Portuguese Republic Government of PortugalPortuguese: Governo de PortugalLogo for the XXIV Government of the Portuguese RepublicOverviewEstablished24 September 1834; 189 years ago (1834-09-24)StatePortuguese RepublicLeaderPrime MinisterAppointed byPresident of the RepublicMain organCouncil of MinistersMinistries17Responsible toAssembly of the RepublicHeadquartersOfficial Residence of the Prime MinisterEstrela, LisbonWebsiteportugal.gov.pt This arti...

Country-rap Origens estil√≠sticas M√ļsica country, hip hop, rock Contexto cultural D√©cada de 1980 nos EUA Instrumentos t√≠picos Vocal, guitarra, bateria, baixo el√©trico - caixa de ritmos. rabeca, steel guitar Outros t√≥picos Hip hop alternativo Country-rap √© um subg√™nero da m√ļsica popular fundindo a m√ļsica country com o estilo de hip hop, tendo sido criado h√° aproximadamente 20 anos.[1] O estilo tamb√©m √© conhecido como hick-hop, hill hop, hip hopry e country hop-hop. Entre seus prin...
