Срце тајге
| |||||||||||||||||||||||||||||||||||||
Read other articles:
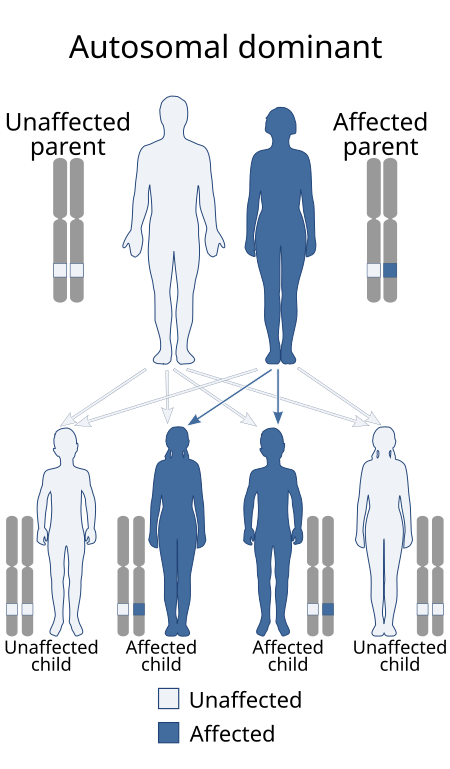
Medical conditionDarier's diseaseOther namesDarier disease, Darier–White disease,[1] Dyskeratosis follicularis,[1] and Keratosis follicularis[2]: 523 [3]: 567 Linear Darier's diseaseSpecialtyMedical genetics Darier's disease (DAR) is a rare, inherited skin disorder that presents with multiple greasy, crusting, thick brown bumps that merge into patches.[4] It is an autosomal dominant disorder discovered by French d...

This article relies largely or entirely on a single source. Relevant discussion may be found on the talk page. Please help improve this article by introducing citations to additional sources.Find sources: Ștefan Golescu – news · newspapers · books · scholar · JSTOR (August 2020) Ștefan GolescuMinister of Foreign AffairsIn office1 March 1867 – 5 August 1867MonarchCarol I of RomaniaPreceded byGeorge Barbu ȘtirbeiSucceeded byAlexandru Teriac...

Cinta IndahGenre Drama Roman PembuatMultivision PlusSutradaraSridhar JettyPemeran Sandra Dewi Anjasmara Samuel Zylgwyn Ayu Diah Pasha Citra Anggun Tommy Kurniawan Olla Ramlan Robby Shine Soraya Anggraeni Endy Arfian Maya Adilla Jiseph Hakim Cok Simbara Penggubah lagu temaDewa 19Lagu pembukaMunajat Cinta oleh Dewa 19Lagu penutupMunajat Cinta oleh Dewa 19Penata musikJoseph S. DjafarNegara asalIndonesiaBahasa asliBahasa IndonesiaJmlh. musim2Jmlh. episodeSeason 1: 121Season 2: 60Total: 181...

Indian television series Sahib Biwi GulamGenreDramaBased onSaheb Bibi Golamby Bimal MitraDirected byAmitava BhattacharyaIndraneil GoswamiCreative directorRituparno GhoshStarringsee belowTheme music composerRaju SinghOpening themeSahib Biwi Gulam by Sapna MukherjeeCountry of originIndiaOriginal languageHindiNo. of seasons1No. of episodes104ProductionProducersPallavi Chatterjee Tripti SharmaProduction locationKolkata, West BengalCinematographyVivek BanerjeeCamera setupMulti-cameraRunning timeAp...

العلاقات المجرية اللاوسية المجر لاوس المجر لاوس تعديل مصدري - تعديل العلاقات المجرية اللاوسية هي العلاقات الثنائية التي تجمع بين المجر ولاوس.[1][2][3][4][5] مقارنة بين البلدين هذه مقارنة عامة ومرجعية للدولتين: وجه المقارنة المجر لاوس المس�...

Bagian dari seri tentangGereja KatolikBasilika Santo Petrus, Kota Vatikan Ikhtisar Paus (Fransiskus) Hierarki Sejarah (Lini Masa) Teologi Liturgi Sakramen Maria Latar Belakang Yesus Penyaliban Kebangkitan Kenaikan Gereja Perdana Petrus Paulus Bapa-Bapa Gereja Sejarah Gereja Katolik Sejarah Lembaga Kepausan Konsili Ekumene Magisterium Empat Ciri Gereja Satu Gereja Sejati Suksesi Apostolik Organisasi Takhta Suci Kuria Romawi Dewan Kardinal Konsili Ekumene Lembaga Keuskupan Gereja Latin Gereja-G...

Saint Eugene de MazenodSt. Eugene de MazenodUskup; Pendiri Oblat Maria Immakulata (OMI)Lahir(1782-08-01)1 Agustus 1782Aix-en-Provence, PrancisMeninggal21 Mei 1861(1861-05-21) (umur 78)Marseille, PrancisDihormati diGereja Katolik RomaBeatifikasi19 Oktober 1975 oleh Paus Paulus VIKanonisasi3 Desember 1995 oleh Paus Yohanes Paulus IITempat ziarahShrine of Notre Dame de la Garde, Marseille, FrancePestaMay 21Pelindungdysfunctional families Saint Eugene de Mazenod (1 Agustus 1782 –&...

Sant'Ignazio di AntiochiaIcona raffigurante il martirio di sant'Ignazio. Vescovo, martire e Padre della Chiesa Nascita35 circa Morte107 circa Venerato daTutte le Chiese che ammettono il culto dei santi Santuario principalele reliquie sono conservate nella basilica di San Clemente, a Roma RicorrenzaChiese cattolica, sira, evangelica e anglicana: 17 ottobre; messa tridentina 1º febbraio)Chiese ortodossa, copta e armena; 2 gennaio Attributivescovo sbranato dai leoni o in catene, palm...

Piatto in ceramica di İznik con tulipani e rosette, 1540-1550. British Museum[1] La ceramica di İznik, che prende il nome dalla città omonima, sita a ovest dell'Anatolia, dove veniva fabbricata, è una ceramica di grande pregio che veniva prodotta fra il tardo XV e il XVII secolo. Indice 1 Storia 1.1 Ruolo della porcellana cinese 1.2 Confusione sulla manifattura di İznik 1.3 İznik e Kütahya 2 Periodo iniziale 2.1 Prime ceramiche di İznik (metà del XIV secolo) 2.2 Mileto (XIV-X...

この項目には、一部のコンピュータや閲覧ソフトで表示できない文字が含まれています(詳細)。 数字の大字(だいじ)は、漢数字の一種。通常用いる単純な字形の漢数字(小字)の代わりに同じ音の別の漢字を用いるものである。 概要 壱万円日本銀行券(「壱」が大字) 弐千円日本銀行券(「弐」が大字) 漢数字には「一」「二」「三」と続く小字と、「壱」「�...

2004 British television documentary series This article needs additional citations for verification. Please help improve this article by adding citations to reliable sources. Unsourced material may be challenged and removed.Find sources: British Isles – A Natural History – news · newspapers · books · scholar · JSTOR (October 2007) (Learn how and when to remove this message) British Isles – A Natural HistoryThe British Isles DVD coverGenreNature doc...

British statesman (1792–1861) The Right HonourableSir James GrahamBt GCB PCHome SecretaryIn office6 September 1841 – 30 June 1846MonarchVictoriaPrime MinisterSir Robert PeelPreceded byThe Marquess of NormanbySucceeded bySir George GreyFirst Lord of the AdmiraltyIn office22 November 1830 – 7 June 1834MonarchWilliam IVPrime MinisterThe Earl GreyPreceded byThe Viscount MelvilleSucceeded byThe Lord AucklandIn office30 December 1852 – 13 March 1855Monarch...

Urban development in locations generating cost savings This article has multiple issues. Please help improve it or discuss these issues on the talk page. (Learn how and when to remove these template messages) This article is written like a personal reflection, personal essay, or argumentative essay that states a Wikipedia editor's personal feelings or presents an original argument about a topic. Please help improve it by rewriting it in an encyclopedic style. (January 2018) (Learn how and whe...

County in Georgia, United States County in GeorgiaTerrell CountyCountyTerrell County Courthouse in DawsonLocation within the U.S. state of GeorgiaGeorgia's location within the U.S.Coordinates: 31°47′N 84°26′W / 31.78°N 84.44°W / 31.78; -84.44Country United StatesState GeorgiaFoundedFebruary 16, 1856; 168 years ago (1856)Named forWilliam TerrellSeatDawsonLargest cityDawsonArea • Total338 sq mi (880 km2) ...

أليسو فيجو الإحداثيات 33°36′58″N 117°44′40″W / 33.616191666667°N 117.74442777778°W / 33.616191666667; -117.74442777778 [1] تاريخ التأسيس 2001 تقسيم إداري البلد الولايات المتحدة[2][3] التقسيم الأعلى مقاطعة أورانج خصائص جغرافية المساحة 17.921214 كيلومتر مربع19.352006 ك�...

History of anarchist involvement with nationalism Part of a series onAnarchism History Outline Schools of thought Feminist Green Primitivist Social ecology Total liberation Individualist Egoist Free-market Naturist Philosophical Mutualism Postcolonial African Black Queer Religious Christian Jewish Social Collectivist Parecon Communist Magonism Without adjectives Methodology Agorism Illegalism Insurrectionary Communization Expropriative Pacifist Platformism Especifismo Relationship Syndicalist...
Cet article est une ébauche concernant les transports en commun et la France. Vous pouvez partager vos connaissances en l’améliorant (comment ?) selon les recommandations des projets correspondants. Compagnie française des transports régionaux Logotype de la CFTR Un bus de la ligne 401 du réseau de bus de Saint-Quentin-en-Yvelines. Création 2015 Dates clés 1908 : création de la Services automobiles de la vallée de Chevreuse (SAVAC)1953 : création des Cars Lacroix S...

American actress and singer (1896–1971) Edith DayDay in 1923BornEdith Marie Day(1896-04-10)April 10, 1896Minneapolis, Minnesota, U.S.DiedMay 1, 1971(1971-05-01) (aged 75)London, England, U.K.Occupation(s)Actress, singerYears active1916–1962Spouses Carle E. Carleton (m. 1919; div. 1922) Pat Somerset (m. 1923; div. 1927) Henry Horne ChildrenOne son by 2nd husband Edith Day (born...

Chen Deming陈德铭 Presiden Asosiasi untuk Hubungan Antar Selat TaiwanPetahanaMulai menjabat 26 April 2013PendahuluChen YunlinPenggantiPetahanaMenteri Perdagangan RRTMasa jabatanDesember 2007 – 16 Maret 2013PendahuluBo XilaiPenggantiGao Hucheng Informasi pribadiLahirTanggal tidak terbaca. Angka tahun harus memiliki 4 digit (gunakan awalan nol untuk tahun < 1000). (usia Kesalahan ekspresi: Operator < tak terduga)Shanghai, Republik TiongkokKebangsaan TiongkokPartai p...

In matematica, in particolare in analisi complessa, si definisce funzione meromorfa su un sottoinsieme aperto D {\displaystyle {\mathcal {D}}} del piano complesso una funzione che è olomorfa su tutto D {\displaystyle {\mathcal {D}}} ad esclusione di un insieme di punti isolati che sono poli della funzione stessa. Ogni funzione meromorfa su D {\displaystyle {\mathcal {D}}} può essere espressa come rapporto di due funzioni olomorfe (con la funzione denominatore diversa dalla costante 0) defin...