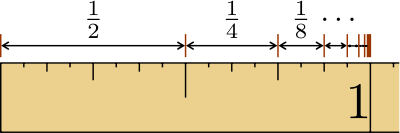
Geometrična vrsta
|
Read other articles:

Diagram fasies metamorfik pada grafik tekanan - suhu. Fasies metamorfik adalah susunan atau sekumpulan mineral - mineral metamorfik yang terbentuk dibawah tekanan dan suhu yang sama.[1] Susunannya memiliki kondisi yang khas sesuai dengan area dengan temperatur dan tekanan tertentu .[1] Batuan yang mengandung mineral - mineral tertentu pada grafik dapat dikaitkan dengan situasi tektonik, waktu, dan tem-at tertentu di sejarah geologi area tersebut.[1] Batas - batas antar...

Wangsa Karoling Wangsa Pipin Pipin Tua (ca. 580–640) Grimoald Tua (616–656) Kildebert Si Anak Angkat (wafat 662) Wangsa Arnulf Arnulf dari Metz (582–640) Ansegisel (wafat 662 atau 679) Klodulf dari Metz (wafat 696 atau 697) Pipin dari Herstal (635-714) Grimoald Muda (wafat 714) Drogo dari Champagne (670–708) Teudoald (wafat 741) Wangsa Karoling Karel Martel (686–741) Karloman (wafat 754) Pipin Si Pendek (714–768) Karloman I (751–771) Karel Agung (742–814) Pipin Si Bungkuk (768...

Benjamin IngrossoIngrosso pada 2018Nama asalBenjamin Daniele Wahlgren IngrossoLahir14 September 1997 (umur 26)Danderyd, Kabupaten Stockholm, SwediaPekerjaanPenyanyipenulis laguTahun aktif2006–sekarangSitus webbenjaminingrossoofficial.com Benjamin Daniele Wahlgren Ingrosso (lahir 14 September 1997) adalah seorang penyanyi dan penulis lagu asal Swedia. Saat masih kecil, ia tampil dalam peran utama dalam beberapa musikal. Pada 2006, ia memenangkan Lilla Melodifestivalen dengan ...

Radio station in West Branch, MichiganWBMIWest Branch, MichiganBroadcast area[1]Frequency105.5 MHzBrandingClassic Hit Country 105-5ProgrammingFormatClassic countryAffiliationsMichigan Radio NetworkOwnershipOwnerCF Broadcasting, LLCHistoryCall sign meaningWest Branch MichiganTechnical informationFacility ID29288ClassAERP6,000 wattsHAAT91 meters (299 ft) WBMI is an American radio station, licensed to West Branch, Michigan, the seat of government for Ogemaw County. The station broadcasts at...

Wallace BeeryLahirWallace Fitzgerald Beery(1885-04-01)1 April 1885Clay County, Missouri, Amerika SerikatMeninggal15 April 1949(1949-04-15) (umur 64)Beverly Hills, California, Amerika SerikatSebab meninggalHeart attackMakamForest Lawn Memorial Park, GlendalePekerjaanPemeran, Penyanyi, SutradaraTahun aktif1913–1949Suami/istriGloria Swanson (m. 1916; bercerai 1919) Rita Gilman (m. 1924; berc...

Town in County Armagh, Northern Ireland Human settlement in Northern IrelandPortadownIrish: Port an DúnáinScots: Portadoun[1] or Portadoon[2]St Mark's Church of Ireland in central PortadownLocation within Northern IrelandPopulation32,926 (2021 estimate)Irish grid referenceJ008537• Belfast24 mi (39 km)• Dublin74 mi (119 km)DistrictArmagh City, Banbridge and CraigavonCountyCounty ArmaghCountryNorthern IrelandSovereign state...

McArdle Laboratory for Cancer Research The McArdle Laboratory for Cancer Research is a basic cancer research facility located on the University of Wisconsin–Madison campus in Madison, Wisconsin. It houses the university's Department of Oncology .[1] The staff of the McArdle Laboratory numbers approximately 200. Twenty-eight faculty members lead research groups focused on various fields such as cancer virology, signal transduction, cell cycle, cancer genetics, and carcinogenesis.[...

British-American screenwriter, comedian, musician, director, and actor For the Law Lord, see Christopher Guest, Baron Guest. The Right HonourableThe Lord Haden-GuestGuest in 2016Member of the House of Lords Lord TemporalIn officeApril 8, 1996 – November 11, 1999Hereditary peeragePreceded byThe 4th Baron Haden-Guest Personal detailsBornChristopher Haden-Guest (1948-02-05) 5 February 1948 (age 76)New York City, U.S.Spouse Jamie Lee Curtis (m. 1984)...

American political party founded by Theodore Roosevelt Progressive Party The bull moose was the party's official mascotChairTheodore RooseveltFounded1912; 112 years ago (1912)Dissolved1920; 104 years ago (1920)Split fromRepublican PartyPreceded byLincoln–Roosevelt LeagueMerged intoRepublican Party (majority)Succeeded byCalifornia Progressive PartyHeadquartersWashington, D.C., U.S.IdeologyProgressivism[1]Radicalism[2] ...
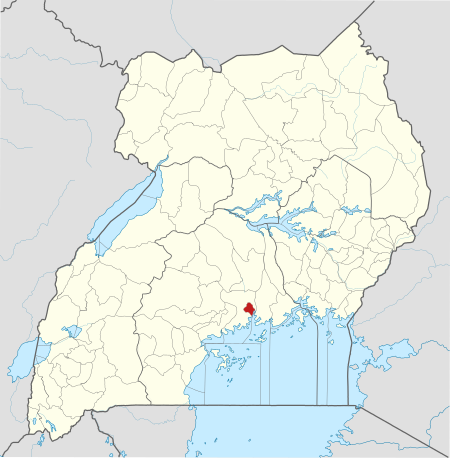
Private hospital in Uganda Not to be confused with International Hospital Kampala. Hospital in Central Region, UgandaKampala HospitalKampala HospitalGeographyLocation6C Makindu Close, Kololo, Kampala, Central Region, UgandaCoordinates00°19′59″N 32°35′04″E / 0.33306°N 32.58444°E / 0.33306; 32.58444OrganisationCare systemPrivateTypeGeneralServicesBeds100HistoryOpened2007; 17 years ago (2007)LinksWebsiteHomepageOther linksList of hospitals in...

Indian cricketer (born 1944) Syed KirmaniPersonal informationFull nameSyed Mujtaba Hussain KirmaniBorn (1949-12-29) 29 December 1949 (age 74)Madras, Madras State, IndiaBattingRight-handedRoleBatsman, Wicket-keeperRelationsSadiq Kirmani (son)International information National sideIndia (1976–1986)Test debut (cap 138)24 January 1976 v New ZealandLast Test2 January 1986 v AustraliaODI debut (cap 17)21 February 1976 v New ZealandLast ODI...

This article may rely excessively on sources too closely associated with the subject, potentially preventing the article from being verifiable and neutral. Please help improve it by replacing them with more appropriate citations to reliable, independent, third-party sources. (October 2015) (Learn how and when to remove this message) United StatesUnder Secretary of Homeland Securityfor Science and TechnologyIncumbentDimitri Kusnezovsince September 29, 2022Formation2003Websitewww.dhs.gov/s...

Koordinat: 50°33′24″N 55°11′29″E / 50.55667°N 55.19139°E / 50.55667; 55.19139 Akrab АкрабАкрабскийاكرابNegara KazakhstanProvinsiAktobeKetinggian111 m (364 ft)Zona waktuUTC+5 (Waktu Kazakhstan Barat) • Musim panas (DST)UTC+5 (Waktu Kazakhstan Barat) Akrab (juga dkenal sebagai Aqyrap[1] (bahasa Rusia: Акрабский, Akrabskiy, bahasa Kazakh: Акраб, Akrab, اكراب)) adalah sebuah kota d...

French statesman (1619–1683) For his son, see Jean-Baptiste Colbert, Marquis de Seignelay. Jean-Baptiste ColbertLord of Vandières and CernayPortrait de Jean-Baptiste Colbert (1655)by Philippe de ChampaigneFirst Minister of StateIn office9 March 1661 – 6 September 1683MonarchLouis XIVPreceded byJules Raymond MazarinSucceeded byThe Marquis of LouvoisSecretary of State of the NavyIn office7 March 1669 – 6 September 1683MonarchLouis XIVPreceded byThe Marquis of FresnesSuc...

Bruno PesaolaPesaola alla guida della Fiorentina fra gli anni 60 e 70 del XX secoloNazionalità Argentina Italia (dal 1953) Altezza165[1] cm Peso74 kg Calcio RuoloAllenatore (ex attaccante) Termine carriera1962 - giocatore1985 - allenatore CarrieraGiovanili 1939-1944 River Plate Squadre di club1 1944-1946 Dock Sud84 (26)1947-1950 Roma90 (20)1950-1952 Novara64 (15)1952-1960 Napoli240 (27)1960-1961 Genoa20 (5)1961-1962 Scafatese? (?) Nazional...

Pathogen resistance to medications This article is about pathogen resistance to the effects of drugs. For human resistance to the effects of drugs, see Drug tolerance. An illustrative diagram explaining drug resistance. Drug resistance is the reduction in effectiveness of a medication such as an antimicrobial or an antineoplastic in treating a disease or condition.[1] The term is used in the context of resistance that pathogens or cancers have acquired, that is, resistance has evolved...

German Open Hamburg 2016Sport Tennis Data11 - 17 luglio Edizione110ª CategoriaATP Tour 500 SuperficieTerra rossa LocalitàAmburgo, Germania CampioniSingolare Martin Kližan Doppio Henri Kontinen / John Peers 2015 2017 Il German Open 2016 è stato un torneo di tennis giocato sulla terra rossa. È stata la 110ª edizione dell'evento che fa parte della categoria ATP Tour 500 nell'ambito dell'ATP World Tour 2016. Si è giocato all'Am Rothenbaum di Amburgo, in Germania, dall'11 al 17 luglio 2016....

Namen von Apries Horusname Wah-ib-Re Nebtiname Wah-ib-Re Goldname Se-wadj-taui S-w3ḏ-t3.w(j) Der die beiden Länder gedeihen lässt Thronname Haa-ib-Re Ḥˁˁ-jb-Rˁ Mit jubelndem Herzen, ein Re Eigenname Wah-ib-Re W3ḥ-jb-Rˁ Mit beständigem Willen, ein Re Griechisch bei Manetho Quaphris Apries (ägyptisch Wahibre, hebräisch חָפְרַע [hɔɸˈraː] Hophra) gehörte als altägyptischer Pharao (König) sowie vierter Herrscher der 26. Dynastie der Saïten-Dynastie an. Er regierte vo...

University in Kenya KCA UniversityTypeprivateEstablished1989 KCA University (KCAU)Vice-ChancellorProf. Isaiah WakindikiLocationNairobi, Kenya1°15′11″S 36°51′36″E / 1.252936°S 36.860136°E / -1.252936; 36.860136Websitehttps://www.kcau.ac.ke KCA University (KCAU) is a private, non-profit institution that was founded in July 1989 as the Kenya College of Accountancy (KCA) by the Institute of Certified Public Accountants of Kenya (ICPAK) to improve the quality of...

Pour les articles homonymes, voir Jordan. Cet article est une ébauche concernant une localité du Montana. Vous pouvez partager vos connaissances en l’améliorant (comment ?) selon les recommandations des projets correspondants. JordanGéographiePays États-UnisÉtat MontanaComté comté de Garfield (siège)Superficie 0,87 km2 (2010)Surface en eau 0 %Altitude 793 mCoordonnées 47° 19′ N, 106° 55′ ODémographiePopulation 356 hab. (2020)Dens...









![{\displaystyle {\begin{aligned}&{\text{Naj je }}s=1+k+k^{2}+k^{3}+\cdots +k^{n-1}.\\[4pt]&{\text{Potem je }}ks=k+k^{2}+k^{3}+k^{4}+\cdots +k^{n}.\\[4pt]&{\text{In }}s-ks=s(1-k)=1-k^{n},{\text{ tako, da je }}s={\frac {1-k^{n}}{1-k}}.\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/aca3fdf78887d8effa77e973a044514a21ceab3b)


![{\displaystyle {\begin{aligned}&{\text{Naj je }}s=1+k+k^{2}+k^{3}+\cdots .\\[4pt]&{\text{Potem je }}ks=k+k^{2}+k^{3}+k^{4}+\cdots .\\[4pt]&{\text{In }}s-ks=1,{\text{ tako, da je }}s={\frac {1}{1-k}}.\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/50148b066b392038aa8b75ecafd1b7ca9fbc0e14)
![{\displaystyle {\begin{aligned}&1\,+\,k\,+\,k^{2}\,+\,k^{3}\,+\,\cdots \\[3pt]&=\;\lim _{n\rightarrow \infty }\left(1\,+\,k\,+\,k^{2}\,+\,\cdots \,+\,k^{n}\right)\\&=\;\lim _{n\rightarrow \infty }{\frac {1-k^{n+1}}{1-k}}\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/9ab1e1cb7745bc4af9ded82bd6c8877c951145f1)
