![]() Graf funkcije absolutne vrednosti realnega števila x
Graf funkcije absolutne vrednosti realnega števila x
Absolútna vrédnost (redko tudi módul) nekega realnega ali kompleksnega števila je v matematiki elementarna funkcija, ki predstavlja njegovo oddaljenost od številskega izhodišča (točke 0) na številski premici oziroma v kompleksni ravnini. Absolutno vrednost po navadi označimo z navpičnim oklepajem | |.
Absolutna vrednost poljubnega števila je vedno nenegativno število.
Realna števila
Absolutna vrednost realnega števila ni odvisna od njegovega predznaka.

Zgled:  in
in  ter
ter  .
.
Velja:
- |a| ≤ b, če in samo če -b ≤ a ≤ b
- |a| ≥ b, če in samo če a ≤ -b ali a ≥ b
Kompleksna števila
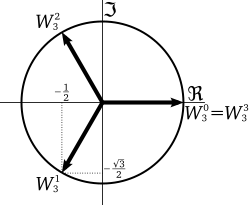 Kompleksna števila z absolutno vrednostjo 1 ležijo na enotski krožnici
Kompleksna števila z absolutno vrednostjo 1 ležijo na enotski krožnici
Če imamo kompleksno število  , kjer sta
, kjer sta  ,
potem je absolutna vrednost
,
potem je absolutna vrednost  , kar predstavlja razdaljo od števila z do točke 0 v kompleksni ravnini. Torej,
, kar predstavlja razdaljo od števila z do točke 0 v kompleksni ravnini. Torej,  .
.
Kompleksna števila, ki imajo enako absolutno vrednost, ležijo na krožnici s središčem v izhodišču.
Značilnosti absolutne vrednosti
Absolutna vrednost ima v realnem in v kompleksnem naslednje značilnosti:
- |a| ≥ 0
- |a| = 0, če in samo če a = 0.
- |ab| = |a||b|
- |a/b| = |a| / |b| (če b ≠ 0)
- |a+b| ≤ |a| + |b| (trikotniška neenakost)
- |a-b| ≥ ||a| − |b||
Poleg tega velja v realnem še  ,
v kompleksnem pa
,
v kompleksnem pa  .
.
Vektorji
Absolutna vrednost vektorja je drugo ime za dolžino vektorja.
Zgled: absolutno vrednost trirazsežnega vektorja  izračunamo po formuli:
izračunamo po formuli:

Programiranje
V programskih jezikih je funkcija abs(a) (za realna števila) običajno vgrajena, sicer pa jo lahko enostavno sprogramiramo (zgled v pascalu):
function abs(a:integer):integer;
begin
if (a >= 0) then abs := a
else abs := -a;
end;