Эффект Керра
|
Read other articles:

August EigruberAugust Eigruber pada tahun 1938 Gauleiter Reichsgau OberdonauMasa jabatan22 Mei 1938 – 5 Mei 1945Reichsstatthalter Reichsgau OberdonauMasa jabatan1 April 1940 – 5 Mei 1945Landeshauptmann Austria HuluMasa jabatan14 Mei 1938 – 1 April 1940 PendahuluHeinrich GleissnerPenggantiJabatan dihapuskan Informasi pribadiLahir(1907-04-16)16 April 1907Steyr, AustriaMeninggal28 Mei 1947(1947-05-28) (umur 40)Penjara Landsberg, Landsberg am LechSebab k...

GaumontJenisPublicKode emitenEuronext: GAMIndustriMotion picturesDidirikan1895KantorpusatNeuilly-sur-Seine, FranceTokohkunciLéon Gaumont, Nicolas SeydouxProdukMotion picturestelevision programsfilm distributionPendapatan € 119.5 million (2011)[1]Laba bersih € 26.7 million (2011)[1]Total aset € 451.5 million (2011)[1]Total ekuitas € 255.9 million (2011)[1]Karyawan173 (2011)[1]AnakusahaGaumont AnimationGaumont International TelevisionLes Cin...

Basilika Bunda dari Walsingham[1]Basilika Minor Tempat Ziarah Nasional Bunda dari WalsinghamChapel of Saint Catherine of AlexandriaInggris: Basilica of Our Lady of WalsinghamBasilika Bunda dari Walsingham52°52′52″N 0°51′12″E / 52.88112°N 0.85331°E / 52.88112; 0.85331Koordinat: 52°52′52″N 0°51′12″E / 52.88112°N 0.85331°E / 52.88112; 0.85331LokasiHoughton Saint GilesNegara Britania Raya InggrisDenomina...

Psychedelic drug DOET redirects here. For the book, see The Design of Everyday Things. 2,5-Dimethoxy-4-ethylamphetamineClinical dataOther names2,5-dimethoxy-4-ethylamphetamineLegal statusLegal status AU: S9 (Prohibited substance) BR: Class F2 (Prohibited psychotropics)[1] CA: Schedule I DE: Anlage I (Authorized scientific use only) UK: Class A US: Schedule I UN: Psychotropic Schedule I Identifiers IUPAC name 1-(4-Ethyl-2,5-dimethoxyphenyl)propan...

Michael OlindoMichael pada tahun 2021LahirMichael James Olindo15 Maret 2001 (umur 23)Jakarta, IndonesiaPekerjaanPemeranTahun aktif2015—sekarangTinggi175 cm (5 ft 9 in)[1] Michael James Olindo (lahir 15 Maret 2001) adalah aktor dan mantan pebasket berkebangsaan Indonesia. Michael memulai karier sebagai atlet dengan bergabung dalam klub basket Victoria Basketball Club, kemudian di tahun 2017 Michael terpilih untuk masuk dalam Tim nasional bola basket Indonesi...

Eyalet di SilistraEyalet di Silistra - LocalizzazioneL'eyalet di Silistra nel 1609 Dati amministrativiNome completoEyalet-i Silistra Lingue ufficialiturco ottomano Lingue parlateturco ottomano, bulgaro, rumeno, moldavo, ucraino CapitaleSilistraÖzi Dipendente daImpero ottomano PoliticaForma di StatoEyalet Forma di governoEyalet elettivo dell'Impero ottomano Capo di StatoSultani ottomani Nascita1593 Fine1864 Territorio e popolazioneBacino geograficoTurchia, Bulgaria, Romania, Moldova, Ucraina ...

Синелобый амазон Научная классификация Домен:ЭукариотыЦарство:ЖивотныеПодцарство:ЭуметазоиБез ранга:Двусторонне-симметричныеБез ранга:ВторичноротыеТип:ХордовыеПодтип:ПозвоночныеИнфратип:ЧелюстноротыеНадкласс:ЧетвероногиеКлада:АмниотыКлада:ЗавропсидыКласс:Пт�...

Peyman MaādiMaadi pada 2019Lahir30 Juli 1970 (umur 53)New York City, Amerika SerikatKebangsaanIran-AmerikaPekerjaan Pemeran penulis naskah sutradara Tahun aktif2000–kiniKarya terkenalA SeparationAbout Elly Life and a Day Just 6.5 Walnut TreeSuami/istriFaranak GhavanlouAnak2[1]Situs webpaymanmaadi.com Paymān Maādi, juga dikenal sebagai Peymān Moādi (Persia: پیمان معادی) adalah seorang pemeran, penulis naskah dan sutradara Iran-Amerika Serikat. Ia dik...
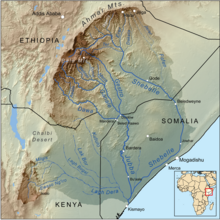
Sungai JubbaPeta aliran lembah sungai Jubba/ShebelleLokasiNegaraSomaliaEtiopiaCiri-ciri fisikHulu sungai - lokasiPertemuan Sungai Dawa dan Sungai Ganale Dorya - koordinat4°10′38″N 42°04′51″E / 4.1771°N 42.0809°E / 4.1771; 42.0809 Muara sungai - lokasiLaut Somali - koordinat0°14′58″S 42°37′51″E / 0.2495°S 42.6307°E / -0.2495; 42.6307Koordinat: 0°14′58″S 42°37′51�...

この項目には、一部のコンピュータや閲覧ソフトで表示できない文字が含まれています(詳細)。 数字の大字(だいじ)は、漢数字の一種。通常用いる単純な字形の漢数字(小字)の代わりに同じ音の別の漢字を用いるものである。 概要 壱万円日本銀行券(「壱」が大字) 弐千円日本銀行券(「弐」が大字) 漢数字には「一」「二」「三」と続く小字と、「壱」「�...

Intermediate appellate courts of Texas The Texas Courts of Appeals are part of the Texas judicial system. In Texas, all cases appealed from district and county courts, criminal and civil, go to one of the fourteen intermediate courts of appeals, with one exception: death penalty cases. The latter are taken directly to the Texas Court of Criminal Appeals, the court of last resort for criminal matters in the State of Texas. The highest court for civil and juvenile matters is the Texas Supreme C...

متحف برج الساعة إحداثيات 21°25′09″N 39°49′31″E / 21.419091°N 39.825376°E / 21.419091; 39.825376 معلومات عامة الموقع مكة المكرمة الدولة السعودية معلومات أخرى الموقع الإلكتروني الموقع الرسمي تعديل مصدري - تعديل متحف برج الساعة هو متحف فلكي يقع في شرفة برج الساعة، بمكة...

В Википедии есть статьи о других людях с такой фамилией, см. Чернов; Чернов, Евгений. Евгений Чернов Общая информация Полное имя Евгений Александрович Чернов Родился 23 октября 1992(1992-10-23)[1] (31 год)Томск, Россия Гражданство Россия Рост 180[2] см Позиция защитник Инфо�...

This article may need to be rewritten to comply with Wikipedia's quality standards. You can help. The talk page may contain suggestions. (August 2009) Three Bugs Fringe Theatre (or 3BUGS) is a society of the University of Birmingham Guild of Students. Set up in 2003 by Stephen Makin and Michael Wood, its primary purpose is to allow University of Birmingham Students to take productions to the Edinburgh Festival Fringe each summer. 2015 productions In 2015 3Bugs performed a sell out physical th...

Fujinomoristazione ferroviaria藤森 Vista della stazione LocalizzazioneStato Giappone LocalitàFushimi-ku, Kyoto Coordinate34°57′24.39″N 135°46′12.23″E34°57′24.39″N, 135°46′12.23″E Linee● Linea principale Keihan StoriaStato attualeIn uso Attivazione1910 CaratteristicheTipoStazione di superficie passante Binari2 OperatoriFerrovie Keihan InterscambiBus Statistiche viaggiatorial giorno14.836 (2009) all'anno- FonteKeihan Fujinomori Modifica dati su Wikidata ...

Pierre Roux-FreissinengPierre Roux-Freissineng en 1932FonctionsSénateur de la Troisième République31 décembre 1933 - 31 décembre 1944Député de l'Algérie française30 novembre 1919 - 23 janvier 1934Bâtonnierà partir de 1909Conseiller municipalOranà partir de 1909BiographieNaissance 27 mai 1863MarseilleDécès 20 décembre 1952 (à 89 ans)MarseilleNationalité françaiseActivités Homme politique, avocatAutres informationsParti politique Radicaux indépendantsDistinction Officie...

欧鲁菲努Ouro Fino市镇欧鲁菲努在巴西的位置坐标:22°16′58″S 46°22′08″W / 22.2828°S 46.3689°W / -22.2828; -46.3689国家巴西州米纳斯吉拉斯州面积 • 总计533.795 平方公里(206.099 平方英里)海拔908 公尺(2,979 英尺)人口 • 總計32,365人 • 密度60.6人/平方公里(157人/平方英里) 欧鲁菲努(葡萄牙语:Ouro Fino)是巴西米纳斯吉�...

GrapheneOS GrapheneOSのホーム画面開発者 GrapheneOSチームOSの系統 Android(Linux)開発状況 開発中ソースモデル オープンソース初版 2019年4月 (5年前) (2019-04)最新安定版 2024061400[1] / 14 6月 2024リポジトリ github.com/GrapheneOS/platform_manifest 対象市場 プライバシーとセキュリティを重視したスマートフォンアップデート方式 OTAアップデート、手動パッケージ管理 APKベー�...

Chinese electric car Motor vehicle Li MegaOverviewManufacturerLi AutoAlso calledLixiang MegaProduction2024–presentAssemblyChina: BeijingBody and chassisClassMinivanBody style5-door minivanLayoutDual-motor, all-wheel-drivePowertrainElectric motorPermanent magnet synchronousPower output400 kW (536 hp; 544 PS)Battery102.7 kWh CATL Qilin ternary lithium batteryRange710 km (441 mi) (CLTC)Plug-in chargingDC:520 kW (official), 552 kW (actual)V2L:3....

1963 studio album by Kenny Burrell with the Brother Jack McDuff QuartetCrash!Studio album by Kenny Burrell with the Brother Jack McDuff QuartetReleased1963RecordedJanuary 8 and February 26, 1963StudioVan Gelder Studio, Englewood Cliffs, New JerseyGenreJazzLabelPrestigePR 7347ProducerOzzie CadenaKenny Burrell chronology Midnight Blue(1963) Crash!(1963) Lotsa Bossa Nova(1963) Brother Jack McDuff chronology Somethin' Slick!(1963) Crash!(1963) Brother Jack McDuff Live!(1963) Crash! is an ...




































