Частичный куб
|
Read other articles:
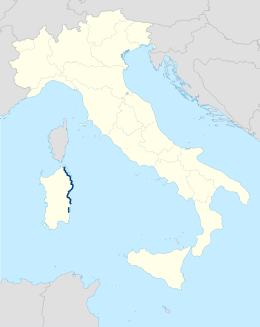
Strada statale 125 Orientale SardaLocalizzazioneStato Italia Regioni Sardegna Province CagliariSud Sardegna Nuoro Sassari DatiClassificazioneStrada statale InizioSS 554 presso Quartucciu FineSS 133 presso Palau Lunghezza354,250[1] km Provvedimento di istituzioneLegge 17 maggio 1928, n. 1094 GestoreTratte ANAS: dal km 0,000 (Cagliari) al km 51,880 (Nuraghe Asoru), dal km 86,794 (Cantoniera di San Giorgio) al km 106,000 (Tertenia), dal km 132,380 (Bari Sardo) al...
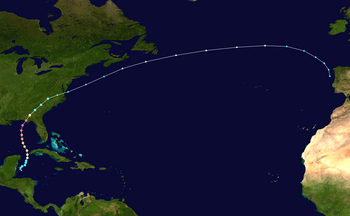
Category 5 Atlantic hurricane in 2018 This article is about the 2018 Atlantic hurricane. For other storms of the same name, see List of storms named Michael. Hurricane Michael Michael at peak intensity shortly before landfall on the Florida Panhandle on October 10Meteorological historyFormedOctober 7, 2018ExtratropicalOctober 11, 2018DissipatedOctober 16, 2018Category 5 hurricane1-minute sustained (SSHWS/NWS)Highest winds160 mph (260 km/h)Lowest pressure919 mbar (hPa); 27....

Departments of Peru This article is about the Peruvian region. For other uses, see Lambayeque (disambiguation). This article needs additional citations for verification. Please help improve this article by adding citations to reliable sources. Unsourced material may be challenged and removed.Find sources: Department of Lambayeque – news · newspapers · books · scholar · JSTOR (March 2008) (Learn how and when to remove this template message) Department i...

Pour les articles homonymes, voir Bave. Sécrétion de la salive dans les canaux des glandes salivaires. La salive est un liquide biologique sécrété par les glandes salivaires, à l'intérieur de la bouche chez la plupart des animaux. La salivation est la production de la salive, tandis que l'insalivation est l'imprégnation des aliments par la salive au cours de leur passage dans la bouche et de leur mastication. Certains animaux ont une salive pouvant devenir allergène pour l'humain (a...

Questa voce o sezione sugli argomenti scrittori italiani e drammaturghi italiani non cita le fonti necessarie o quelle presenti sono insufficienti. Puoi migliorare questa voce aggiungendo citazioni da fonti attendibili secondo le linee guida sull'uso delle fonti. Segui i suggerimenti del progetto di riferimento. Alessandro De Stefani nel 1954 Alessandro De Stefani (Cividale del Friuli, 1º gennaio 1891 – Roma, 13 maggio 1970) è stato un commediografo, scrittore, sceneggiatore e regis...

Form of social benefit Child benefit or children's allowance is a social security payment which is distributed to the parents or guardians of children, teenagers and in some cases, young adults. A number of countries operate different versions of the program. In most countries, child benefit is means-tested and the amount of child benefit paid is usually dependent on the number of children one has. Conditions for payment A number of conditional cash transfer programs in Latin America and Afri...

Assedio di Torinoparte della guerra di successione spagnolaProgetto francese di attacco a TorinoData14 maggio - 7 settembre 1706 LuogoTorino, Piemonte EsitoVittoria austro-sabauda Schieramenti Francia Spagna Ducato di Savoiain seguito ai rinforzi Sacro Romano Impero Comandanti Duca de la Feuillade Filippo II d'Orléans Ferdinand de Marsin † Vittorio Amedeo II di Savoia Virico von Daunin seguito ai rinforzi Principe Eugenio di Savoia Leopoldo I di Anhalt-Dessau Giovanni Battista d'Embser Eff...

此條目可参照英語維基百科相應條目来扩充。 (2021年5月6日)若您熟悉来源语言和主题,请协助参考外语维基百科扩充条目。请勿直接提交机械翻译,也不要翻译不可靠、低品质内容。依版权协议,译文需在编辑摘要注明来源,或于讨论页顶部标记{{Translated page}}标签。 约翰斯顿环礁Kalama Atoll 美國本土外小島嶼 Johnston Atoll 旗幟颂歌:《星條旗》The Star-Spangled Banner約翰斯頓環礁�...

PK Park built in 2009, home of the Eugene Emeralds. There are six stadiums in use by Northwest League baseball teams. The oldest stadium is Funko Field (1947) in Everett, Washington, home of the Everett AquaSox. The newest stadium is Hillsboro Ballpark (2013) in Hillsboro, Oregon, home of the Hillsboro Hops. One stadium was built in the 1940s, two in the 1950s, and one in each of the 1990s, 2000s, and 2010s. The highest seating capacity is 6,803 at Avista Stadium in Spokane, Washington, wher...

Airport in Reggio di CalabriaReggio di Calabria AirportAeroporto di Reggio di CalabriaIATA: REGICAO: LICRSummaryAirport typePublic & MilitaryOperatorSacal S.p.A.ServesReggio di Calabria, MessinaLocationReggio di CalabriaBuilt1939OccupantsV Reparto di Volo della Polizia di StatoElevation AMSL29.26 m / 95.99 ftCoordinates38°04′19″N 15°39′13″E / 38.07194°N 15.65361°E / 38.07194; 15.65361Websitesacal.it/en/reggio-calabria-airport/MapREGShow m...
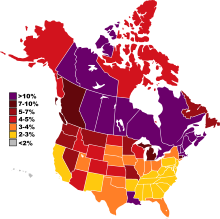
Americans of French birth or descent For the language spoken by some of these people, see American French. French AmericansFranco-Américains (French)French Americans and French Canadians as percent of population by state and province.[a]Total populationIncluding French-Canadian: 8,053,902 (2.4%) alone or in combination 2,211,954 (0.7%) French or French-Canadian alone Excluding French-Canadian: 6,464,646 (1.9%) alone or in combination 1,505,143 (0.5%) French alone 2021 estimates, self...
Fortification in Australia Tomaree Head FortificationsLocation of Tomaree Head Fortifications in New South WalesLocation2 Shoal Bay Road, Shoal Bay, New South Wales, AustraliaCoordinates32°42′53″S 152°11′12″E / 32.7148°S 152.1866°E / -32.7148; 152.1866 New South Wales Heritage RegisterOfficial nameTomaree Head Fortifications; Tomaree Head; head Battery; Tomaree Battery and Stephens BatteryTypestate heritage (built)Designated22 October 2010Reference no....

artikel ini perlu dirapikan agar memenuhi standar Wikipedia. Tidak ada alasan yang diberikan. Silakan kembangkan artikel ini semampu Anda. Merapikan artikel dapat dilakukan dengan wikifikasi atau membagi artikel ke paragraf-paragraf. Jika sudah dirapikan, silakan hapus templat ini. (Pelajari cara dan kapan saatnya untuk menghapus pesan templat ini) Waduk (bahasa Inggris: reservoir, dari bahasa Prancis: réservoir, yang berarti wadah, tempat penyimpanan) adalah danau buatan atau danau ...
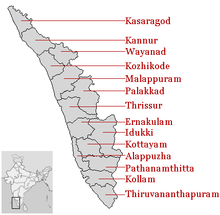
Distrik di KeralaDistrik di KeralaKategoriDistrikLetakKeralaJumlah wilayah14 distrikPendudukWayanad – 846.637 (terendah); Malappuram – 4.494.998 (tertinggi)LuasAlappuzha – 1415 km2 (terkecil); Palakkad – 4482 km2 (terluas)PemerintahanPemerintah Kerala Kerala terbagi ke dalam 14 distrik.[1] Berdasarkan kesamaan geografis, sejarah, dan budaya, distrik-distrik yang ada pada umumnya dikelompokkan menjadi dua bagian – Kerala Utara yang mencakup Kasaragod, Kannur, Wayanad[2 ...

هذه المقالة يتيمة إذ تصل إليها مقالات أخرى قليلة جدًا. فضلًا، ساعد بإضافة وصلة إليها في مقالات متعلقة بها. (يوليو 2011) الشك العلمي هو ممارسة للتشكيك في صحة ادعاءات تفتقر إلى الأدلة التجريبية أو استنساخ، كجزء من قاعدة السعي المنهجي «توسيع المعرفة المعتمدة». على سبيل المثال، ر...

Main article: History of Oregon Volume 1, Oregon Historical Society Quarterly, 1900 For a useful starting point goto Oregon Encyclopedia of History and Culture (2022). Not yet in print format; it is online here with 2000 articles. The following published works deal with the cultural, political, economic, military, biographical and geologic history of pre-territorial Oregon, Oregon Territory and the State of Oregon.[1] Surveys of Oregon history Bancroft, Hubert Howe (1886). History of...
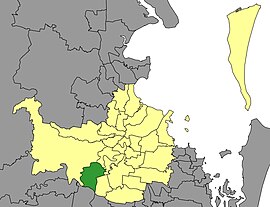
Brisbane City Council ward Australian electorate Jamboree WardMPSarah HuttonPartyLiberal NationalNamesakeJamboree HeightsElectors31,037 (2024)[1] The Jamboree Ward is a Brisbane City Council ward covering Jamboree Heights, Darra, Jindalee, Middle Park, Mt Ommaney, Riverhills, Seventeen Mile Rocks, Sinnamon Park, Wacol and parts of Ellen Grove and Oxley.[2] Councillors for Jamboree Ward Member Party Term Phil Denman Liberal 1976–1991 Christine Watson Libera...

Professional practitioner of engineering and its subclasses For other uses, see Engineer (disambiguation). EngineerMechanical engineer Joel Steinkraus and systems engineer Farah Alibay (right) from NASA Jet Propulsion Laboratory hold a full-scale mockup of Mars Cube OneOccupationNamesEngineerOccupation typeProfessionActivity sectorsApplied scienceDescriptionCompetenciesMathematics, science, design, analysis, critical thinking, engineering ethics, project management, engineering economics, cre...

Medical museum in West Yorkshire, EnglandThackray Museum of MedicineMuseum entranceEstablishedMarch 1997LocationBeckett Street, Leeds, West Yorkshire, EnglandTypeMedical museumCEOEdward AppleyardWebsitewww.thackraymuseum.co.uk The Thackray Museum of Medicine in Leeds, West Yorkshire, England, is a museum of the history of medicine adjacent to St James's University Hospital. It opened in March 1997 as the Thackray Medical Museum. In 1998 it won Museum of the Year and has other awards includin...

Pour les articles homonymes, voir Mondonville (homonymie). Jean-Joseph Cassanéa de Mondonville Mondonville par Maurice Quentin de La Tour Données clés Naissance 25 décembre 1711 Narbonne, Royaume de France Décès 8 octobre 1772 (à 60 ans) Belleville, Royaume de France Activité principale compositeur Style Musique baroque Conjoint Anne-Jeanne Boucon modifier Jean-Joseph Cassanéa de Mondonville par Charles-Nicolas Cochin et Delatre. Jean-Joseph Cassanéa de Mondonville, baptisé �...









