Теорема Ролля
|
Read other articles:

Artikel ini perlu diwikifikasi agar memenuhi standar kualitas Wikipedia. Anda dapat memberikan bantuan berupa penambahan pranala dalam, atau dengan merapikan tata letak dari artikel ini. Untuk keterangan lebih lanjut, klik [tampil] di bagian kanan. Mengganti markah HTML dengan markah wiki bila dimungkinkan. Tambahkan pranala wiki. Bila dirasa perlu, buatlah pautan ke artikel wiki lainnya dengan cara menambahkan [[ dan ]] pada kata yang bersangkutan (lihat WP:LINK untuk keterangan lebih lanjut...

This article needs additional citations for verification. Please help improve this article by adding citations to reliable sources. Unsourced material may be challenged and removed.Find sources: Estádio Martins Pereira – news · newspapers · books · scholar · JSTOR (August 2022) (Learn how and when to remove this template message) Martins PereiraMartins PereiraFull nameEstádio Municipal Martins PereiraLocationAlbergaria-a-Velha, Aveiro state, Portugal...

Smoke-like, fog-like air pollutions For other uses, see Smog (disambiguation). Not to be confused with Smoke. Smog and a sunny day within a 10-day interval in Fanhe, China Part of a series onPollutionAir pollution from a factory Air Air quality index Atmospheric dispersion modeling Chlorofluorocarbon Combustion Exhaust gas Haze Global dimming Global distillation Indoor air quality Ozone depletion Particulates Persistent organic pollutant Smog Soot Volatile organic compound Waste Biological Bi...

Hemodialisis sedang berlangsung Mesin Hemodialisis Hemodialisis berasal dari kata “hemo” artinya darah, dan “dialisis ” artinya pemisahan zat-zat terlarut. Hemodialisis berarti proses pembersihan darah dari zat-zat sampah, melalui proses penyaringan di luar tubuh. Hemodialisis menggunakan ginjal buatan berupa mesin dialisis. Hemodialisis dikenal secara umum dengan istilah cuci darah.[1] Cara kerja Pada hemodialisis darah dikeluarkan dari tubuh pasien dan diedarkan dalam sebuah...

You can help expand this article with text translated from the corresponding article in Polish. (October 2016) Click [show] for important translation instructions. Consider adding a topic to this template: there are already 1,449 articles in the main category, and specifying|topic= will aid in categorization. Do not translate text that appears unreliable or low-quality. If possible, verify the text with references provided in the foreign-language article. You must provide copyri...

Municipality and town in Hidalgo, MexicoNicolás FloresMunicipality and townNicolás FloresLocation in MexicoCoordinates: 20°46′01″N 99°09′05″W / 20.76694°N 99.15139°W / 20.76694; -99.15139Country MexicoStateHidalgoMunicipal seatNicolás FloresArea • Total393.2 km2 (151.8 sq mi)Population (2005) • Total6,202 Nicolás Flores is a town and one of the 84 municipalities of Hidalgo, in central-eastern Mexico. The ...

Questa voce sull'argomento contee del Michigan è solo un abbozzo. Contribuisci a migliorarla secondo le convenzioni di Wikipedia. Contea di TuscolaconteaLocalizzazioneStato Stati Uniti Stato federato Michigan AmministrazioneCapoluogoCaro Data di istituzione1º aprile 1840 TerritorioCoordinatedel capoluogo43°28′N 83°27′W / 43.466667°N 83.45°W43.466667; -83.45 (Contea di Tuscola)Coordinate: 43°28′N 83°27′W / 43.466667°N 83.45°W4...

English journalist and television presenter Jon SnowHonFRIBABornJonathan George Snow (1947-09-28) 28 September 1947 (age 76)Ardingly, EnglandEducationScarborough TECUniversity of LiverpoolOccupation(s)Journalist, television presenter, news anchorYears active1973–presentNotable creditChannel 4 News (1989–2021)Spouse Precious Lunga (m. 2010)PartnerMadeleine Colvin (separated)Children3RelativesGeorge Snow (father)Peter Snow (cousin)Dan Snow (cousin) J...

Edward Clark PotterPhoto of Edward Clark Potter in 1899.LahirEdward Clark Potter(1857-11-26)26 November 1857New London, ConnecticutMeninggal21 Juni 1923(1923-06-21) (umur 65)New London, ConnecticutKebangsaanAmericanPendidikanSchool of the Museum of Fine Arts, Boston, Académie JulianDikenal atassculpture Signature Edward C. Potter Edward Clark Potter (26 November 1857 – 21 Juni 1923) adalah seorang pematung Amerika yang terkenal karena patung berkuda dan hewannya. Karyan...

Stasiun Ambarawa Ambarawa+474,40 m Tampak depan bangunan utama Stasiun Ambarawa, 2023LokasiJalan Stasiun AmbarawaPanjang, Ambarawa, Semarang, Jawa Tengah 50611IndonesiaKoordinat7°15′53″S 110°24′8″E / 7.26472°S 110.40222°E / -7.26472; 110.40222Koordinat: 7°15′53″S 110°24′8″E / 7.26472°S 110.40222°E / -7.26472; 110.40222Ketinggian+474,40 mOperator KAI Wisata Letak km 36+763 lintas Kedungjati–Bringin–Ambarawa km 83+401 l...

Art music of northern regions of the Indian subcontinent Hindustani classical music Concepts Shruti Swara Alankar Raga Tala Thaat Gharana Instruments Melody Vocals Sitar Sarod Surbahar Rudra veena Violin Sarangi Esraj/Dilruba Bansuri Shehnai Santoor Harmonium Jal tarang Rhythm Tabla Pakhawaj Drone Tanpura Shruti box Swarmandal Genres Classical Dhrupad Dhamar Sikh music Khyal Tarana Sadra Semiclassical Thumri Tappa Chaiti Kajri Hori Sawani Dadra Qawwali Ghazal Thaats Bilaval Khamaj Kafi Asavar...
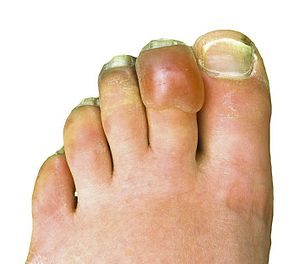
Radang dinginFrostbiteRadang dingin yang terjadi pada jari kaki setelah 2-3 hari mendaki gunungInformasi umumSpesialisasiObat darurat, OrtopediTipeBagian luar, dalam[1]PenyebabSuhu di bawah titik beku[2]Faktor risikoEthanol, merokok, kesehatan mental, obat-obat tertentu, cedera dingin sebelumnya[2]Aspek klinisGejala dan tandaMati rasa, terasa dingin, canggung, warna pucat[2]KomplikasiHipotermia, Sindrom kompartemen[2][1]DiagnosisBerdasarkan geja...

لي دونغ-هوي (بالكورية: 이동휘) معلومات شخصية الميلاد 22 يوليو 1985 (39 سنة)[1] كوريا الجنوبية مواطنة كوريا الجنوبية العشير هو ايون جونغ (2016–)[2] الحياة العملية المدرسة الأم معهد سول للفنون المهنة ممثل أفلام، وممثل تلفزيوني اللغة الأم الكورية...

Musa Pour les articles homonymes, voir Bananier (homonymie). Musa Illustration botanique de Musa ×paradisiaca.Classification de Cronquist (1981) Règne Plantae Sous-règne Tracheobionta Division Magnoliophyta Classe Liliopsida Sous-classe Zingiberidae Ordre Zingiberales Famille Musaceae GenreMusaL., 1753 Classification APG III (2009) Classification APG III (2009) Clade Angiospermes Clade Monocotylédones Clade Commelinidées Ordre Zingiberales Famille Musaceae Le Bananier (Musa) est un genre...

Japanese television channel Television channel NickelodeonLogo without the Japanese writing. 2018–2022CountryJapanBroadcast areaJapanHeadquartersTokyoProgrammingLanguage(s)JapanesePicture format1080i (HDTV)OwnershipOwnerViacomCBS Networks Japan K.K. (ViacomCBS)HistoryLaunchedNovember 15, 1998; 25 years ago (1998-11-15) (original)January 30, 2018; 6 years ago (2018-01-30) (relaunch as a brand for OTT media services)ClosedSeptember 30, 2009; 14 years ago (o...

Liyumen鲤鱼门Shenzhen MetroLokasiDistrik Nanshan, Shenzhen, GuangdongChinaOperatorSZMC (Shenzhen Metro Group)JalurGalat Lua: expandTemplate: template "SZM lines" does not exist.Jumlah peron2 (1 peron pulau)LayananStasiun kereta api Shenzhen Barat (200 meter)KonstruksiJenis strukturBawah tanahSejarahDibuka15 Juni 2011Operasi layanan Lua error in package.lua at line 80: module 'Module:Adjacent stations/SZM' not found. Sunting kotak info • L • BBantuan penggunaan templ...

First President of Lebanon (1890–1964) This article is about the Lebanese president. For the Franco-Lebanese composer, see Bechara El Khoury (composer). Bechara Khalil El Khouryبشارة خليل الخوريOfficial portrait, 19471st President of LebanonIn office22 November 1943 – 18 September 1952Prime MinisterRiad SolhAbdul Hamid KaramiSami SolhSaadi Al MunlaHussein Al OweiniAbdallah El-YafiNazem AkkariSaeb SalamSucceeded byCamille ChamounIn office21 September 1943 –&#...

Владимир Алексеевич Голобуцкийукр. Володимир Олексійович Голобуцький Дата рождения 15 (28) июня 1903 или 28 июля 1903(1903-07-28) Место рождения Великий Бор, Суражский уезд, Черниговская губерния, Российская империя или Великий бор Дата смерти 21 января 1993(1993-01-21) (89 лет) Мест�...

American chemist and physicist (1881–1957) Irving LangmuirBorn(1881-01-31)January 31, 1881[1]Brooklyn, New York, U.S.DiedAugust 16, 1957(1957-08-16) (aged 76)Woods Hole, Massachusetts, U.S.NationalityAmericanAlma materColumbia University University of GöttingenKnown forInventor of the high-vacuum tubeLangmuir isothermLangmuir wavesAwards William H. Nichols Medal (1915, 1920) Hughes Medal (1918) Perkin Medal (1928) Willard Gibbs Award (1930) Nobel Prize in Chemistry (...

المحجوبي أحرضان رئيس الحركة الشعبية تولى المنصبمارس 2006 إنشاء المنصب الأمين العام للحركة الوطنية الشعبية في المنصب1991 – 2006 إنشاء المنصب حل الحزب الأمين العام للحركة الشعبية في المنصب1957 – 1986 إنشاء المنصب محمد العنصر وزير الدفاع الوطني في المنصب1961 – 1964 العاهل الحسن الث...

![{\displaystyle [a,b]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/9c4b788fc5c637e26ee98b45f89a5c08c85f7935)







