Тензор Риччи
|
Read other articles:
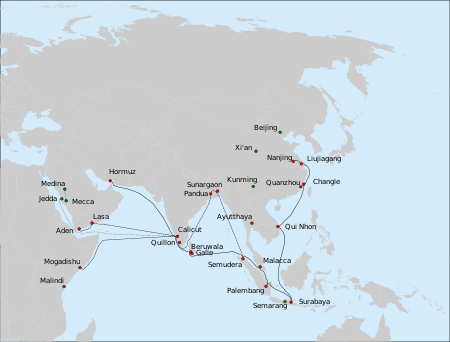
Pelayaran ke-7 armada Cheng Ho. Rute yang memungkinkan dari skuadron Hong Bao ditampilkan sebagai garis putus-putus, berdasarkan pada analisis oleh Edward L. Dreyer.[1] Hong Bao (Hanzi: 洪保; sekitar 1412–1433) adalah seorang kasim Tiongkok yang dikirim ke misi diplomatik seberang laut pada masa pemerintahan Kaisar Yongle dan Kaisar Xuande pada zaman dinasti Ming. Ia dikenal sebagai komandan salah satu skuadron detasemen armada Cheng Ho pada pelayaran ketujuh armada ini ke Sam...

Artikel ini memiliki beberapa masalah. Tolong bantu memperbaikinya atau diskusikan masalah-masalah ini di halaman pembicaraannya. (Pelajari bagaimana dan kapan saat yang tepat untuk menghapus templat pesan ini) artikel ini perlu dirapikan agar memenuhi standar Wikipedia. Masalah khususnya adalah: Kesalahan penggunaan huruf kapital Silakan kembangkan artikel ini semampu Anda. Merapikan artikel dapat dilakukan dengan wikifikasi atau membagi artikel ke paragraf-paragraf. Jika sudah dirapikan, si...

Untuk kegunaan lain, lihat Frankfurt. Frankfurter Rundschau-Haus Frankfurter Rundschau ialah surat kabar harian Jerman, bermarkas di Frankfurt am Main. Pertama kali terbit pada 1 Agustus 1945, sebagai surat kabar pertama di Jerman yang diduduki AS dan kedua di Jerman pascaperang. Kini dimiliki oleh Druck und Verlagshaus Frankfurt am Main GmbH dan mencapai oplah 181.000. Rundschau ialah harian kedua Jerman yang dicetak setelah PD II, dan harian pertama di sektor Amerika. Hans Habe, seorang war...

† Человек прямоходящий Научная классификация Домен:ЭукариотыЦарство:ЖивотныеПодцарство:ЭуметазоиБез ранга:Двусторонне-симметричныеБез ранга:ВторичноротыеТип:ХордовыеПодтип:ПозвоночныеИнфратип:ЧелюстноротыеНадкласс:ЧетвероногиеКлада:АмниотыКлада:Синапсиды�...

MusakhanSajianMenu utamaTempat asalPalestinaDaerahLevantBahan utamaAyam, sumac, bawang bombay, roti taboon, minyak zaitunSunting kotak info • L • BBantuan penggunaan templat ini Media: MusakhanMusakhan (Arab: مسخّن, har. 'sesuatu yang dipanaskan'[1]), juga dikenal sebagai muhammar (Arab: محمر, har. 'lobak'), adalah hidangan Palestina yang terdiri dari ayam panggang yang dipanggang dengan bawang bombay, sumac, merica, k...

Pour les articles homonymes, voir Dimitrov. Grigor Dimitrov Grigor Dimitrov au Tournoi de Washington en 2023. Carrière professionnelle 2008 Nationalité Bulgarie Naissance 16 mai 1991 (32 ans)Haskovo Taille 1,91 m (6′ 3″) Prise de raquette Droitier, revers à une main Entraîneur Daniel Vallverdu Gains en tournois 25 695 250 $ Palmarès En simple Titres 9 Finales perdues 11 Meilleur classement 3e (20/11/2017) En double Titres 0 Finales perdues 1 Meilleur cl...

CSRP2 التراكيب المتوفرة بنك بيانات البروتينOrtholog search: PDBe RCSB قائمة رموز معرفات بنك بيانات البروتين 2CU8 المعرفات الأسماء المستعارة CSRP2, CRP2, LMO5, SmLIM, cysteine and glycine rich protein 2 معرفات خارجية الوراثة المندلية البشرية عبر الإنترنت 601871 MGI: MGI:1202907 HomoloGene: 111061 GeneCards: 1466 علم الوجود الجيني الوظيفة �...

University of PrešovSlovak: Prešovská univerzita Latin: Universitas Presoviensis Photo: Faculty of Greek-Catholic TheologyTypePublicEstablished1997RectorDr. H.c. prof. PhDr. Peter Kónya PhD.Administrative staff1,050Students10,059 (as of 31 October 2012)AddressNámestie legionárov 3, 080 01, Prešov, SlovakiaAffiliationsEUA, The American Chamber of Commerce in the Slovak Republic, Danube Rectors´ ConferenceWebsitewww.unipo.sk The University of Prešov (Slovak: Prešovská univerzita v P...

Species of bird Sunda pygmy woodpecker Conservation status Least Concern (IUCN 3.1)[1] Scientific classification Domain: Eukaryota Kingdom: Animalia Phylum: Chordata Class: Aves Order: Piciformes Family: Picidae Genus: Yungipicus Species: Y. moluccensis Binomial name Yungipicus moluccensis(Gmelin, JF, 1788) Synonyms Picoides moluccensisDendrocopos moluccensis The Sunda pygmy woodpecker (Yungipicus moluccensis), also known as the Sunda woodpecker, is a species of bird in the...

American outlaw Not to be confused with Emmet Dalton, Irish soldier and film producer. Emmett DaltonBooking photo between 1892 and 1893Born(1871-05-03)May 3, 1871[1]Belton, Missouri, U.S.DiedJuly 13, 1937(1937-07-13) (aged 66)Los Angeles, California, U.S.Resting placeKingfisher, Oklahoma, U.S.NationalityAmericanOccupations Outlaw Real estate agent author actor Criminal statusPardoned after 14 years servedAllegianceDalton GangConviction(s)Second-degree murderCriminal penaltyLife i...
2005–2016 geotagging photo sharing service owned by Google PanoramioPanoramio homepageType of sitePhoto sharingAvailable inMultilingualDissolvedNovember 4, 2016; 7 years ago (2016-11-04)OwnerGoogleCreated byJoaquín Cuenca Abela (co-founder)Eduardo Manchón (co-founder)Jose Florido (co-founder)URLwww.panoramio.com CommercialYesRegistrationFreeUsers4.1 millionLaunchedOctober 3, 2005; 18 years ago (2005-10-03)Current statusDefunct Panoramio w...

This is a list of hills in Cornwall based on data compiled in various sources, but particularly the Database of British and Irish Hills, Jackson's More Relative Hills of Britain[1] and the Ordnance Survey 1:25,000 Explorer and 1:50,000 Landranger map series. Many of these hills are important historic, archaeological and nature conservation sites, as well as popular hiking and tourist destinations in the county of Cornwall in southwest England. Colour key Class Prominence Marilyns 150...

The Series of 1902, also known as the Second Bureau Issue, is a set of definitive postage stamps in fourteen denominations ranging between one cent and five dollars, produced by the U. S. Bureau of Engraving and Printing and issued by the United States Post Office. Two denominations appeared in November and December 1902 and the other twelve were released between January and June 1903. These stamps were assigned the Scott Catalogue numbers 300 through 313.[1] Also considered part of t...

Південна Родезія Перша світова війна Антанта Вступ у війну Дата: 1914 Причина: колоніальна залежність від Великої Британії Вихід з війни Дата: 1918 Причина: перемога Антанти Результати Результат: Політичні зміни: отримання від метрополії статусу самоврядної території Збро�...

1931 film This article needs additional citations for verification. Please help improve this article by adding citations to reliable sources. Unsourced material may be challenged and removed.Find sources: Kiki 1931 film – news · newspapers · books · scholar · JSTOR (February 2015) (Learn how and when to remove this message) KikiTheatrical release posterDirected bySam TaylorWritten byPlay:David Belasco André Picard Screenplay:Sam TaylorProduced by...

National constitution of Mongolia Constitution of MongoliaOverviewOriginal titleМонгол УлсынҮндсэн ХуульJurisdictionMongoliaRatified13 January 1992Date effective12 February 1992SystemUnitary semi-presidential constitutional republicGovernment structureBranchesThreeHead of statePresidentChambersUnicameral(State Great Khural)ExecutivePrime Minister led cabinetJudiciaryConstitutional Court Supreme CourtFederalismNoElectoral collegeNoHistoryFirst legislature20 July 1992...

Pour les articles homonymes, voir Roseau (homonymie). Roseau Unicode M017 {{{trans}}} Version hiératique et hiéroglyphique. Le roseau en hiéroglyphes égyptiens, est classifié dans la section M « Végétaux » de la liste de Gardiner ; il y est noté M17. Représentation il représente un plant de canne de Provence (Arundo donax) en fleur. Il est translittéré j, y ou ȝ. Utilisation C'est un idéogramme dans le terme j : « roseaux, feuilles (de roseaux) ...

Myosoricinae Myosoricinae Gambar celurut hutan Myosorex variusTaksonomiFilumChordataKelasMammaliaOrdoEulipotyphlaFamiliSoricidaeSubfamiliMyosoricinae Kretzoi, 1965 GeneraCongosorex Myosorex Surdisorex Myosoricinae adalah sebuah sub-keluarga celurut. Sub-keluarga tersebut merupakan salah satu dari tiga jenis celurut utama, dua sub-keluarga lainnya adalah celurut gigi merah dan celurut gigi putih. Sub-keluarga tersebut hanya salah satu dari tiga sub-keluarga yang khusus ditemukan di selatan Gur...

Para otros usos de este término, véase Málaga (desambiguación). Málaga Provincia de España De izquierda a derecha y de arriba abajo, vista del centro de Málaga, cartel de Marbella, panorámica desde Gibralfaro, caminito del Rey, espeto de sardinas, Tajo de Ronda, vista desde el balcón de Europa, Benalmádena de noche y Torremolinos. BanderaEscudo Coordenadas 36°43′00″N 4°25′00″O / 36.716666666667, -4.4166666666667Capital MálagaIdioma oficial EspañolEntidad...

Esmé StewartEsmé Stewart ritratto da John WeesopDuca di RichmondStemma In carica1655 –1660 PredecessoreJames Stewart, I duca di Richmond SuccessoreCharles Stewart, III duca di Richmond Altri titoliDuca di Lennox Nascita2 novembre 1649 MorteParigi, 10 agosto 1660 (10 anni) Luogo di sepolturaAbbazia di Westminster, Londra DinastiaStewart di Darnley PadreJames Stewart MadreMary Villiers Esmé Stewart, II duca di Richmond e V duca di Lennox (2 novembre 1649 – Parigi, 10 agos...













![{\displaystyle d\mu _{g}={\Big [}1-{\frac {1}{6}}R_{jk}x^{j}x^{k}+O(|x|^{3}){\Big ]}d\mu _{\text{Евклида}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/06dd1baa104e526f70fba77947107a88569190a0)












