Резонанс Лидова — Козаи
|
Read other articles:

Artikel ini bukan mengenai Putri Pariwisata Indonesia. Puteri Indonesia PariwisataDiberikan kepadaPemenang ketiga kontes Puteri IndonesiaNegaraIndonesiaDipersembahkan olehYayasan Puteri IndonesiaDiberikan perdana1995Pemegang gelar saat iniNi Ketut Permata Juliastrid Sari BaliIkhtisarPemegang terbanyakDKI Jakarta, Bali (3)Situs webwww.puteri-indonesia.com Puteri Indonesia Pariwisata (kadang disingkat PI Pariwisata) adalah gelar yang sejak 2006 diberikan kepada pemenang ketiga (runner-up 2...

Football tournament season 2006–07 Football League CupCarling Cup, League CupTournament detailsCountry England WalesTeams92Defending championsManchester UnitedFinal positionsChampionsChelsea (4th title)Runner-upArsenalTournament statisticsTop goal scorer(s)Jermaine EasterJúlio Baptista(6 goals)← 2005–062007–08 → The 2006–07 Football League Cup (known as the Carling Cup for sponsorship reasons) was the 47th staging of the Football League Cup, a knock-o...

العلاقات المارشالية السيراليونية جزر مارشال سيراليون جزر مارشال سيراليون تعديل مصدري - تعديل العلاقات المارشالية السيراليونية هي العلاقات الثنائية التي تجمع بين جزر مارشال وسيراليون.[1][2][3][4][5] مقارنة بين البلدين هذه مقارنة عامة ومر�...

Leo PennLeo Penn (1964)LahirLeo Zalman Penn(1921-08-27)27 Agustus 1921Lawrence, Massachusetts, Amerika SerikatMeninggal5 September 1998(1998-09-05) (umur 77)Santa Monica, California, Amerika SerikatMakamHoly Cross Cemetery, Culver CityKebangsaan Amerika SerikatPekerjaanSutradara televisi, aktorTahun aktif1946–1998Suami/istri Olive Deering (m. 1947; c. 1952) Eileen Ryan (m. 1957) AnakMichael Pe...

Es Castellcomune Es Castell – Veduta LocalizzazioneStato Spagna Comunità autonoma Baleari Provincia Isole Baleari TerritorioCoordinate39°52′43″N 4°17′24″E / 39.878611°N 4.29°E39.878611; 4.29 (Es Castell)Coordinate: 39°52′43″N 4°17′24″E / 39.878611°N 4.29°E39.878611; 4.29 (Es Castell) Altitudine19 m s.l.m. Superficie11,66 km² Abitanti7 892 (2009) Densità676,84 ab./km² Comuni confinantiMahón (Ma...

JAT Airways Penerbangan 367Ringkasan pengebomanTanggal26 Januari 1972RingkasanPengebomanLokasiSrbská Kamenice, CekoslowakiaPenumpang23Awak5Cedera1 (Vesna Vulović)Tewas27Selamat1 pramugari (Vesna Vulović)Jenis pesawatMcDonnell Douglas DC-9-32OperatorJAT Yugoslav AirlinesRegistrasiYU-AHTAsalBandar Udara Stockholm-ArlandaStockholm, SwediaPerhentianBandar Udara KopenhagenKopenhagen, DenmarkPerhentian terakhirBandar Udara ZagrebZagreb, YugoslaviaTujuanBandar Udara BelgradeBelgrade, Yugosla...

Indian ship and submarine company Mazagon Dock Shipbuilders LimitedCompany typePublicTraded asBSE: 543237 NSE: MAZDOCKIndustryShipbuildingFounded1934; 90 years ago (1934)[1]HeadquartersMumbai, Maharashtra, IndiaKey peopleSanjeev Singhal (Chairman & MD)ProductsNaval shipsSubmarines offshore platforms Tankers Bulk carriers Platform supply vessels Patrol boatsServicesShip designShip buildingShip repairRevenue ₹7,827.18 crore (US$980 million) (FY2023...

Voce principale: Unione Sportiva Catanzaro 1929. US Catanzaro 1929Stagione 2022-2023Lo stadio Nicola Ceravolo, campo di casa del Catanzaro Sport calcio Squadra Catanzaro Allenatore Vincenzo Vivarini All. in seconda Andrea Milani Presidente Floriano Noto Serie C1º (promosso in Serie B) Coppa ItaliaTurno preliminare Coppa Italia Serie CQuarti di finale Supercoppa Serie CVincitore Maggiori presenzeCampionato: 3 giocatori (36)Totale: 3 giocatori (38) Miglior marcatoreCampionato: Iemmello (...

2016年美國總統選舉 ← 2012 2016年11月8日 2020 → 538個選舉人團席位獲勝需270票民意調查投票率55.7%[1][2] ▲ 0.8 % 获提名人 唐納·川普 希拉莉·克林頓 政党 共和黨 民主党 家鄉州 紐約州 紐約州 竞选搭档 迈克·彭斯 蒂姆·凱恩 选举人票 304[3][4][註 1] 227[5] 胜出州/省 30 + 緬-2 20 + DC 民選得票 62,984,828[6] 65,853,514[6]...

Street in Melbourne, Victoria, Australia Swan StreetOlympic BoulevardVictoriaLooking west along Olympic Boulevard east of Melbourne Park, just before the tram tracks diverge off-streetWest endEast endCoordinates 37°49′23″S 144°58′35″E / 37.823150°S 144.976318°E / -37.823150; 144.976318 (West end) 37°49′36″S 145°01′22″E / 37.826597°S 145.022757°E / -37.826597; 145.022757 (East end) General informationTypeRoadLength...

Quantitative basis for the informed management of sustainability Trees being felled in Kalimantan, the Indonesian part of Borneo, in 2013, to make way for a new coal mining project Sustainability measurement is a set of frameworks or indicators used to measure how sustainable something is. This includes processes, products, services and businesses. Sustainability is difficult to quantify.[1] It may even be impossible to measure as there is no fixed definition.[2] To measure su...

Political system of Spain Politics of Spain Constitution Constitution Constitutional Court President Cándido Conde-Pumpido Vice President Inmaculada Montalbán Huertas Constitutional history Spanish transition to democracy Human rights Taxation Law Abortion Nationality Capital punishment Life imprisonment The CrownRoyal Household The Monarch (list) Felipe VI Heir presumptive (list) Leonor, Princess of Asturias Royal family Succession to the Spanish throne ExecutiveGovernment of the Nation Pr...

Wesley Clair Mitchellsebelum 1923KebangsaanAmerika SerikatBidangEkonomi politikMakroekonomiMazhabEkonomi institusionalAlma materUniversity of ChicagoDipengaruhiThorstein VeblenJohn DeweyJames L. LaughlinKontribusiRiset empiris mengenai Siklus ekonomi Wesley Clair Mitchell (5 Agustus 1874 – 29 Oktober 1948) adalah seorang ekonom Amerika Serikat yang dikenal atas karyanya mengenai siklus ekonomi dan bantuannya terhadap National Bureau of Economic Research dalam dekade pert...

Mark Tacher مارك تاتشير معلومات شخصية اسم الولادة Mark Tacher Feingold مارك تاتشير فينغولد الميلاد 15 سبتمبر 1977 (العمر 46 سنة)مكسيكو سيتي, المكسيك مواطنة المكسيك أقرباء ألن تاتشير (أخ) الحياة العملية المهنة ممثل, موسيقار اللغات الإسبانية سنوات النشاط 1996–حتى الأن المواقع الموقع ...

US Presidential political appointee White House Deputy Chief of StaffIncumbentAnne Tomasini, Bruce Reed, and Natalie Quilliansince January 20, 2021Executive Office of the PresidentWhite House OfficeReports toWhite House Chief of StaffAppointerPresident of the United StatesWebsitewww.whitehouse.gov The White House deputy chief of staff is officially the top aide to the White House chief of staff, who is the senior aide to the president of the United States. The deputy chief of staff usual...

Beata Villana delle BottiTomba della beata Villana nella basilica di Santa Maria Novella Domenicana NascitaFirenze, 1332 MorteFirenze, 29 gennaio 1360 Venerato daChiesa cattolica Beatificazione1824 da papa Leone XII (conferma del culto) Ricorrenza29 gennaio Manuale Beata Villana delle Botti (Firenze, 1332 – Firenze, 29 gennaio 1360) è stata una religiosa italiana. Indice 1 Biografia 2 Culto 3 Note 4 Bibliografia 5 Altri progetti 6 Collegamenti esterni Biografia Villana delle Bot...

Zimbabwean footballer Rutendo Makore Makore at the 2016 OlympicsPersonal informationDate of birth 30 September 1992 (1992-09-30) (age 32)Place of birth ZimbabweHeight 1.65 m (5 ft 5 in)[1]Position(s) ForwardSenior career*Years Team Apps (Gls)2017–2018 Sporting Huelva 9 (3)International career Zimbabwe *Club domestic league appearances and goals Rutendo Makore (born 30 September 1992) is a Zimbabwean footballer who plays as a forward for the Zimbabwe women's ...

Scottish noble Hugh the Dull (1294 – between 1333 and 1346) was Lord of Douglas, a Scottish nobleman and cleric. The second son of William the Hardy, Lord of Douglas, William Wallace's companion in arms, and Eleanor Ferrers. Hugh's elder brother was Sir James Douglas, a hero of the Wars of Independence, and his younger was Sir Archibald Douglas, Guardian of the realm, and Scots commander at the Battle of Halidon Hill. Early life Hugh of Douglas is first heard of in 1296. Following the forfe...
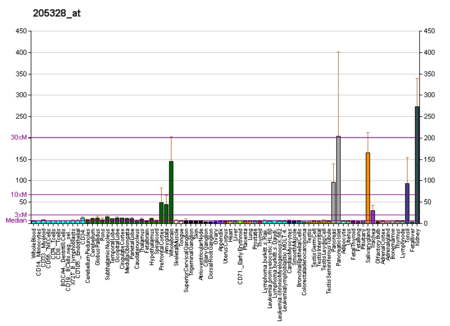
CLDN10 معرفات أسماء بديلة CLDN10, CPETRL3, OSP-L, claudin 10, OSPL, HELIX معرفات خارجية الوراثة المندلية البشرية عبر الإنترنت 617579 MGI: MGI:1913101 HomoloGene: 5076 GeneCards: 9071 علم الوجود الجيني وظائف جزيئية • structural molecule activity• identical protein binding مكونات خلوية • سيتوبلازم• مكون تكاملي للغشاء• موصل خلوي• غشاء• bicellular t...

Masakatsu Takagi at a Nuit Blanche for Toyota in Paris, France Masakatsu Takagi (高木 正勝, Takagi Masakatsu, born 1979) is a musician and filmmaker from Kameoka, Kyoto, Japan.[1] He attended Kyoto University of Foreign Studies, graduating with English. He wrote the score for Mamoru Hosoda's films Wolf Children (2012), The Boy and the Beast (2015) and Mirai (2018).[2] He also wrote the music for the Studio Ghibli documentary The Kingdom of Dreams and Madness (2013). His wo...




